

相控阵天线方向图:线阵波束特性和阵列因数
描述
作者:Peter Delos, Bob Broughton, and Jon Kraft
随着数字相控阵在商业、航空航天和国防应用中的普及,许多从事设计各个方面的工程师对相控阵天线的熟悉程度有限。相控阵天线设计并不新鲜,因为该理论已经发展了几十年;然而,大多数文献都是为精通电磁数学的天线工程师准备的。随着相控阵开始包含更多的混合信号和数字内容,许多工程师可以从对相控阵天线模式的更直观的解释中受益。事实证明,相控阵天线的行为与混合信号和数字工程师每天使用的离散时间采样系统之间存在许多类比。
这些文章的目的不是培养天线设计工程师,而是帮助工程师在相控阵中使用的子系统或组件上工作,以可视化他们的工作如何影响相控阵天线方向图。
光束方向
首先,让我们看一个控制相控阵声束的直观示例。图1提供了波前从两个不同方向撞击四个天线元件的简单图示。在每个天线元件之后的接收路径中应用时间延迟,然后将所有四个信号相加。在图1a中,该时间延迟与波前撞击每个元件的时间差相匹配。在这种情况下,施加的延迟导致四个信号在组合点同相到达。这种相干合并导致合路器输出端的信号更大。在图 1b 中,应用了相同的延迟;但是,在这种情况下,波前垂直于天线元件。施加的延迟现在使四个信号的相位错位,并且合路器的输出显着降低。
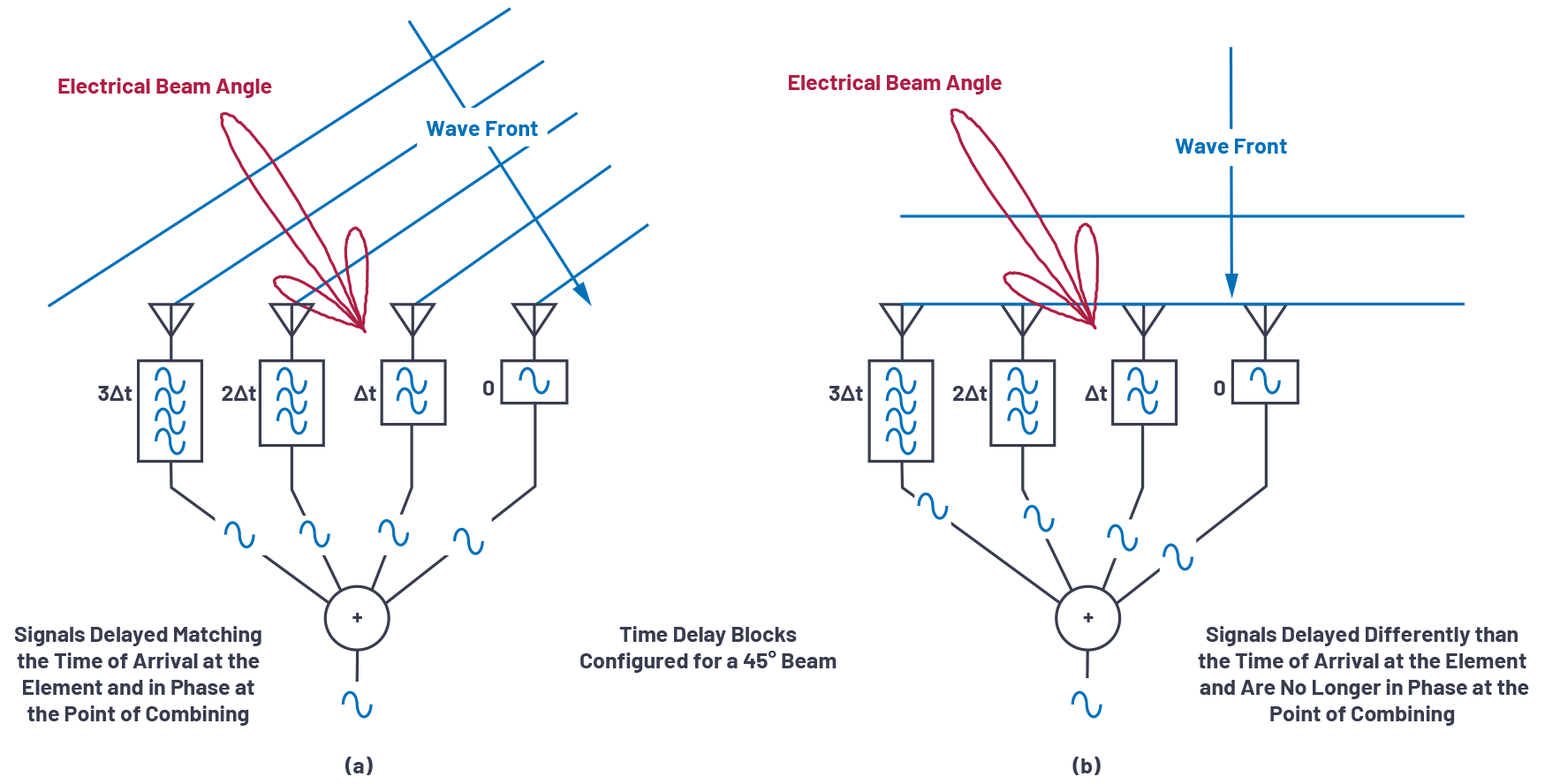
图1.了解转向角。
在相控阵中,时间延迟是声束偏转所需的可量化增量。但是时间延迟也可以通过相移来模拟,这在许多实现中很常见且实用。我们将在光束斜视部分中讨论时间延迟与相移的影响,但现在让我们看一下相移实现,然后推导出具有该相移的光束控制计算。
图2显示了这种使用移相器而不是延时器的相控阵布置。请注意,我们将视线方向 (θ = 0º) 定义为垂直于天线表面。正角 θ 定义为视轴的右侧,负角度定义为视镜的左侧。
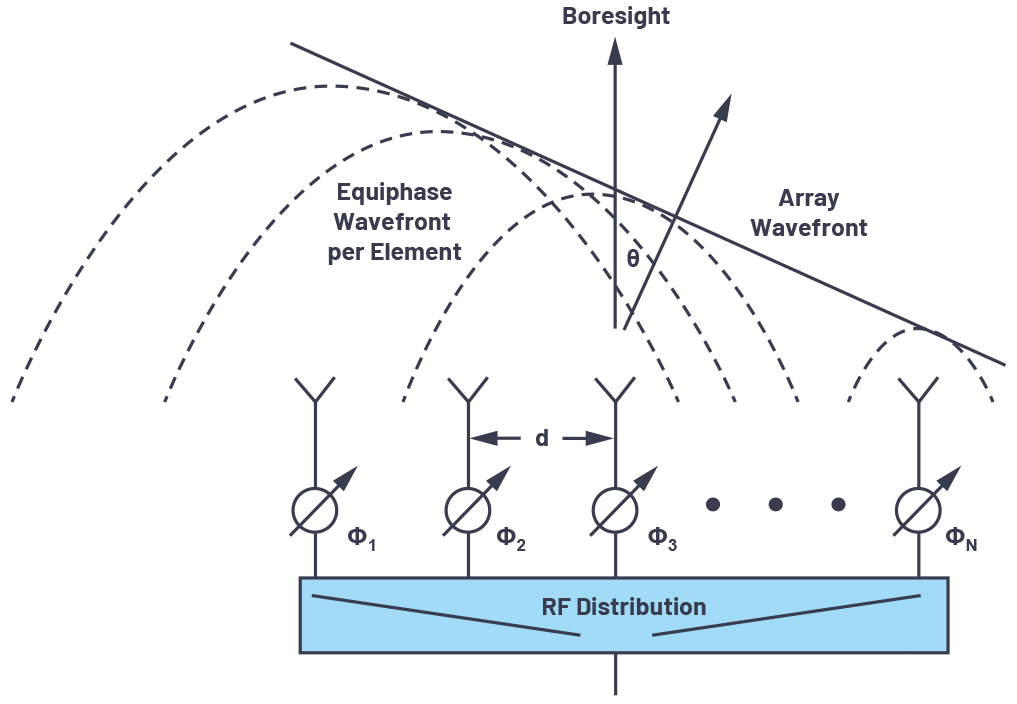
图2.使用RF移相器的相控阵概念。
为了可视化光束控制所需的相移,可以在相邻元件之间绘制一组直角三角形,如图3所示。其中ΔΦ是这些相邻元素之间的相移。
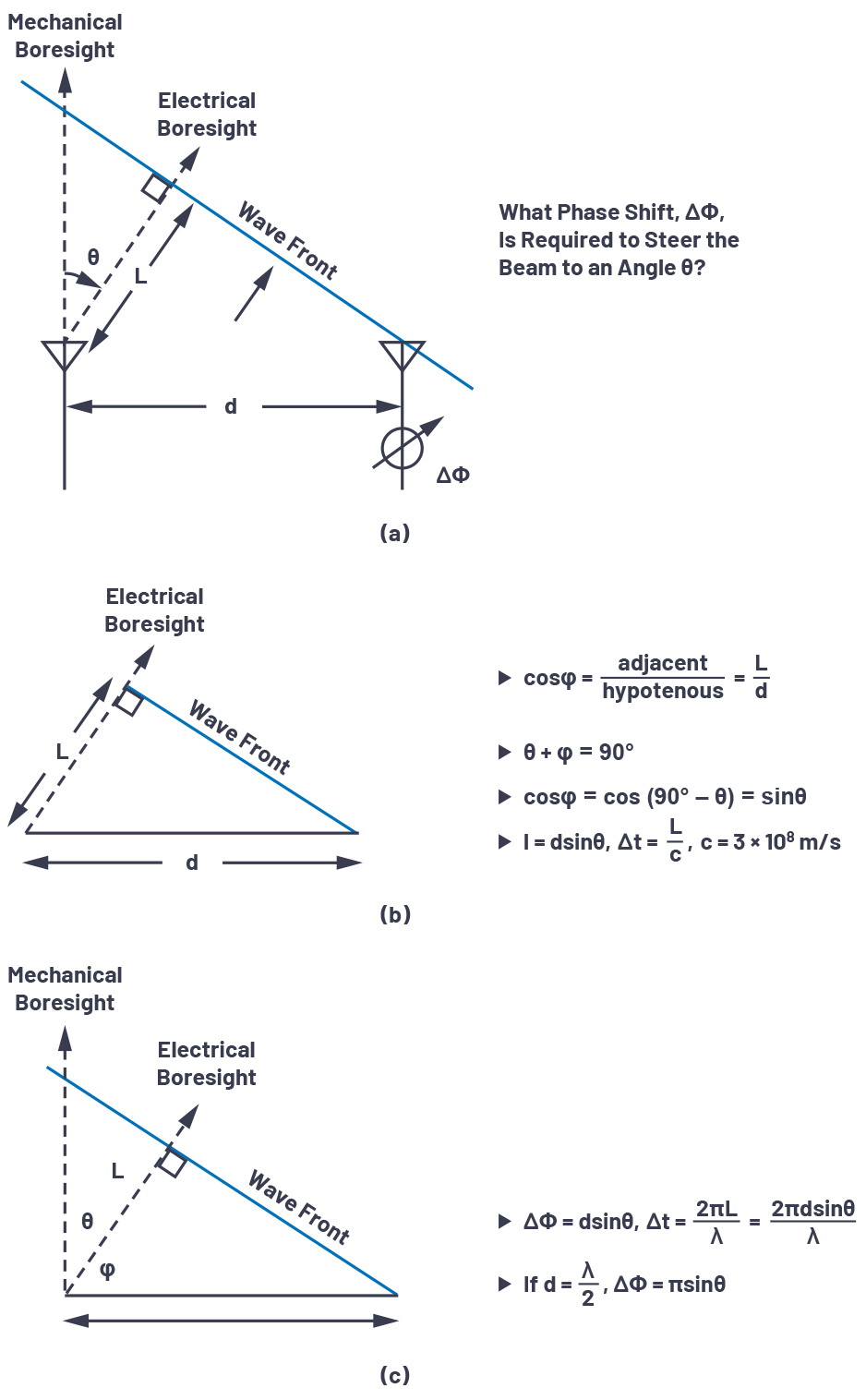
图3.相移ΔΦ与光束转向角的推导。
图 3a 定义了这些元素之间的三角函数,每个元素之间用距离 (d) 分隔。光束指向偏离视线的方向θ,这是与地平线φ的角度。在图 3b 中,我们看到 θ + φ = 90 的总和o. 这允许我们计算L,即波传播的增量距离,因为L = dsin(θ)。控制波束的时间延迟等于波前穿越该距离所需的时间L。如果我们将L视为波长的一小部分,则可以用相位延迟代替该时间延迟。然后可以相对于θ定义ΔΦ的方程,如图3c所示,并在公式1中重复。

如果元件之间的间距正好是信号波长的一半,那么这可以进一步简化为:

让我们用这些方程计算出一个例子。考虑两个相距 15 mm 的天线元件。如果 10.6 GHz 波前距离机械视线 30º,那么两个元件之间的最佳相移是多少?
θ = 30º = 0.52 rad
λ = c/f = (3 × 108米/秒)/10.6 GHz = 0.0283 米
∆Φ = (2π × d × sinθ)/λ = 2π × 0.015 × sin(0.52)/0.0283 m = 1.67 rad = 95º
因此,如果我们的波前到达θ = 30º,那么如果我们将相邻元素的相位移动95º,我们将使两个元素的单个信号相干地相加。这将最大化该方向的天线增益。
为了更好地理解相移如何随光束方向(θ)变化,图4中针对各种条件绘制了这些方程。从这些图表中可以得出一些有趣的观察结果。对于d = λ/2的情况,视线附近有一个大约3比1的斜率,这是公式2中的π乘数。这种情况还显示,晶片之间的完全 180° 偏移提供了理论上的 90° 光束方向偏移。在实践中,对于真实的元素模式,这是无法实现的,但方程确实显示了理论理想。请注意,对于 d > λ/2,再多的相移也无法提供完整的光束偏移。稍后,我们将看到这种情况可能导致天线方向图中出现光栅瓣,并且该图提供了第一个指标,表明 d > λ/2 情况有所不同。
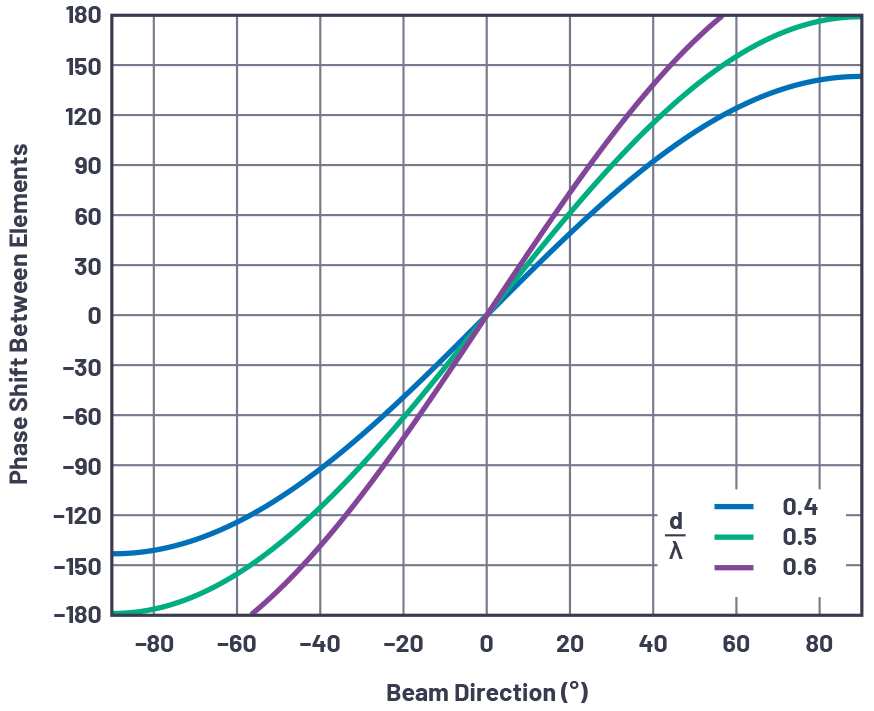
图4.三种d/λ情况下,晶片之间的相移ΔΦ与光束方向(θ)的关系。
均匀间隔的线性阵列
上面开发的方程只适用于两个元素。然而,真正的相控阵可以是分布在二维空间的数千个晶片。但出于我们的目的,让我们只考虑一个维度:线性数组。
线性数组是单个元素宽,有 N 个元素。间距可能会有所不同,但通常是均匀的。因此,在本文中,我们将每个元素之间的间距设置为均匀的距离 d(图 5)。虽然经过简化,但这种均匀间隔的线性阵列模型为深入了解天线方向图在各种条件下的形成方式提供了基础。我们可以进一步应用线性数组的原理来理解二维数组。

图5.均匀间隔的线性阵列 (N = 4)。
近场与远场
那么,我们如何才能将先前为N = 2线性阵列开发的方程应用于N = 10,000线性阵列呢?现在,似乎每个天线元件指向球面波前的角度略有不同,如图6所示。
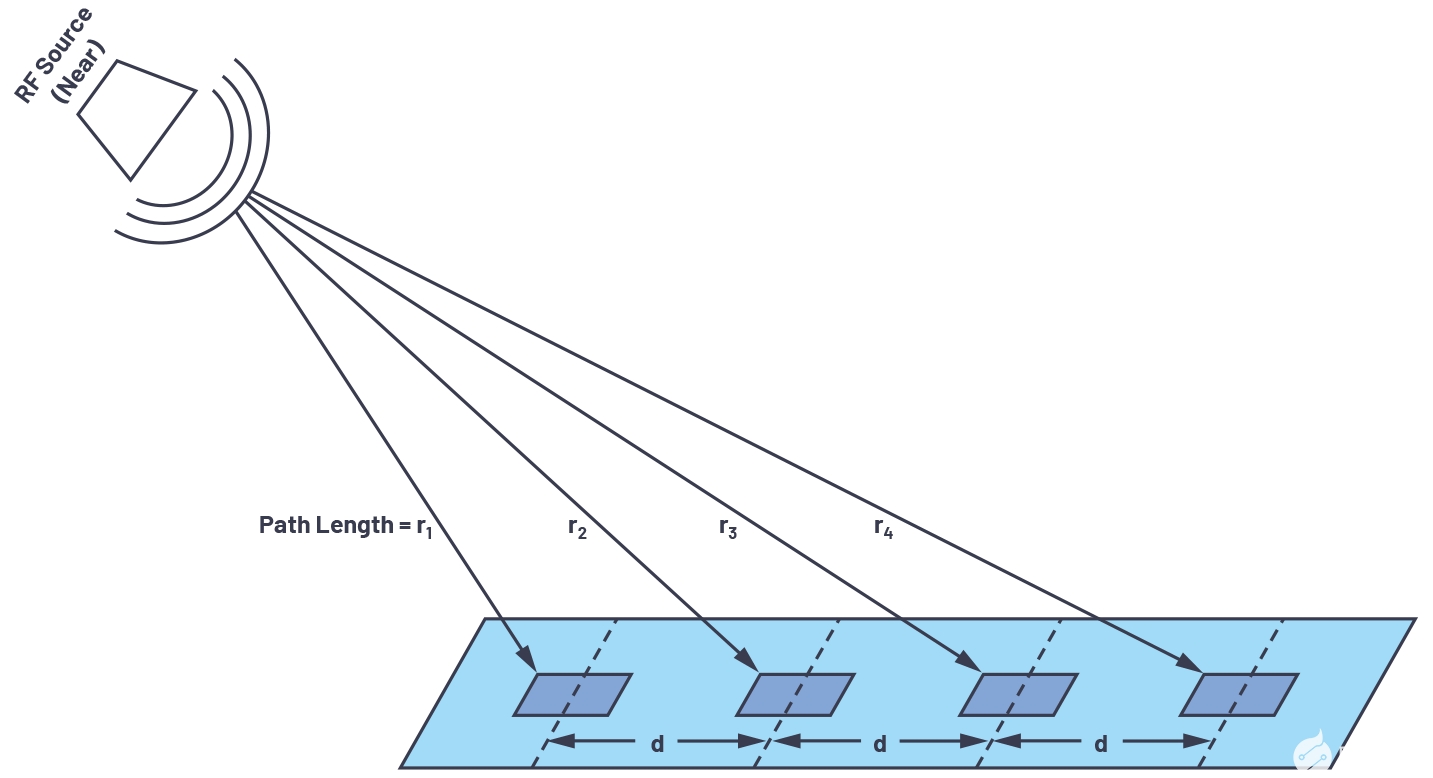
图6.线性阵列附近的射频源。
当RF源靠近时,每个元件的入射角会有所不同。这种情况称为近场。我们可以计算出所有这些角度,有时我们需要这样做来进行天线测试和校准,因为我们的测试设置只能这么大。但是,如果我们只是假设RF源很远,那么我们就会得到图7中的情况。
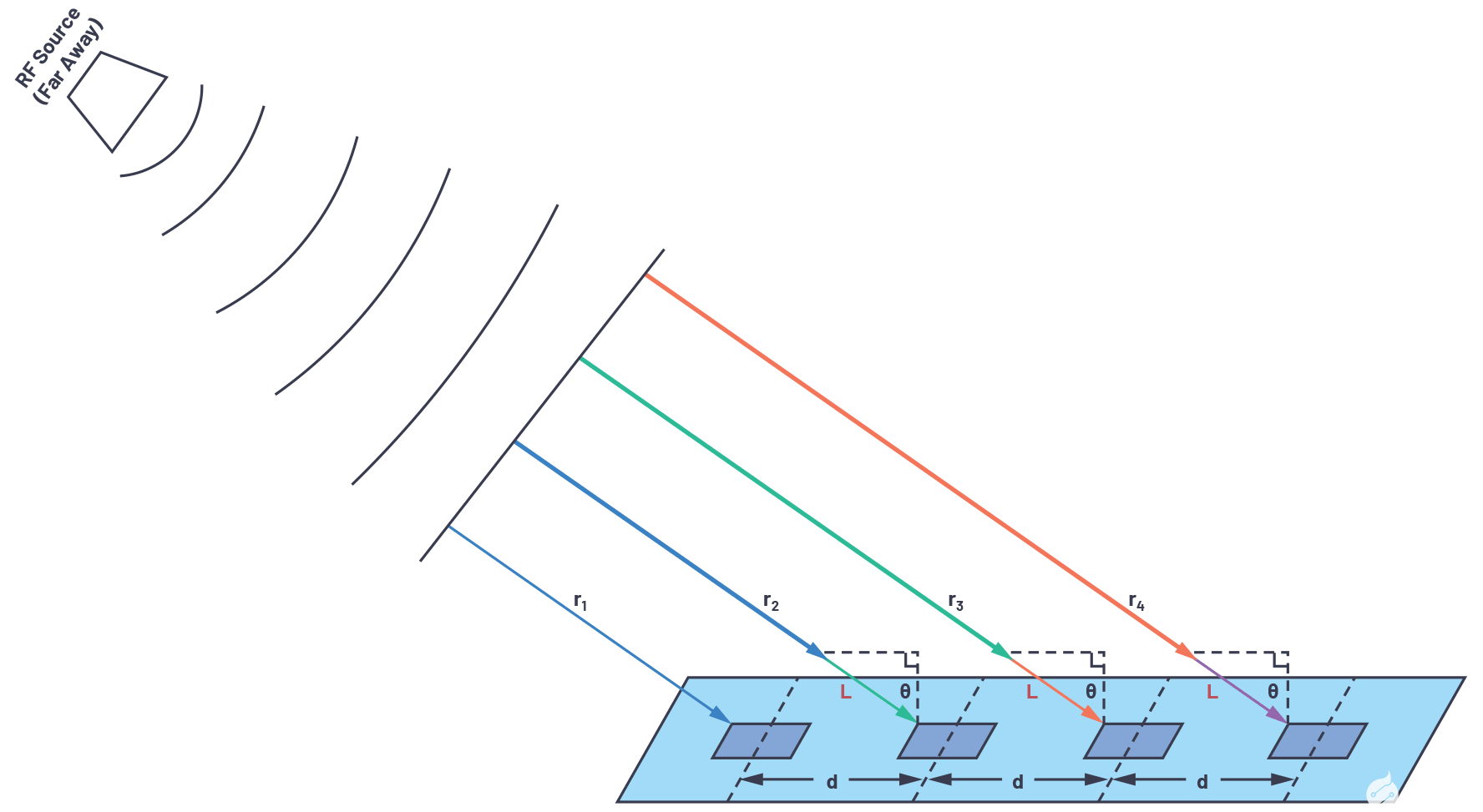
图7.远离线性阵列的射频源。
由于RF源较远,球面波前的大半径导致波传播路径大致平行。因此,我们所有的光束角都是相等的,并且每个相邻单元的路径长度为L = d × sinθ 比其相邻元素长。这简化了数学运算,意味着我们推导出的两个元素方程可以应用于数千个元素,只要它们具有均匀的间距。
但是我们什么时候可以做出远场假设呢?有多远?这有点主观,但一般来说,远场被认为是大于:

其中 D 是天线的直径(((N-1) × d 表示我们的均匀线性阵列)
对于小阵列(小D)或低频(大λ),远场距离很小。但是对于大型阵列(或高频),远场距离可能长达数公里!这使得测试和校准阵列变得困难。对于这些情况,可以使用更详细的近模型,然后将其桥接回远场,实际使用阵列。
天线增益、方向性和孔径
在我们走得太远之前,定义天线增益、方向性和孔径是有帮助的。让我们从澄清增益与方向性开始,因为两者经常互换。天线增益和方向性与各向同性天线相比,各向同性天线是向各个方向均匀辐射的理想天线。方向性是测量的最大功率的比较,P.max,在特定方向上平均向所有方向辐射的功率,P一V.当未定义方向时,方向性由公式4确定。

在比较天线时,方向性是一个有用的指标,因为它定义了聚焦辐射能量的能力。增益具有相同的方向性模式,但增益包括天线损耗。
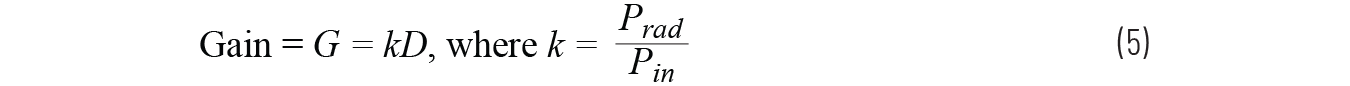
P拉德是辐射的总功率,P在是天线的输入功率,k表示天线辐射过程中的损耗。
接下来,让我们将天线方向图视为三维方向的函数,将方向性视为波束宽度的函数。
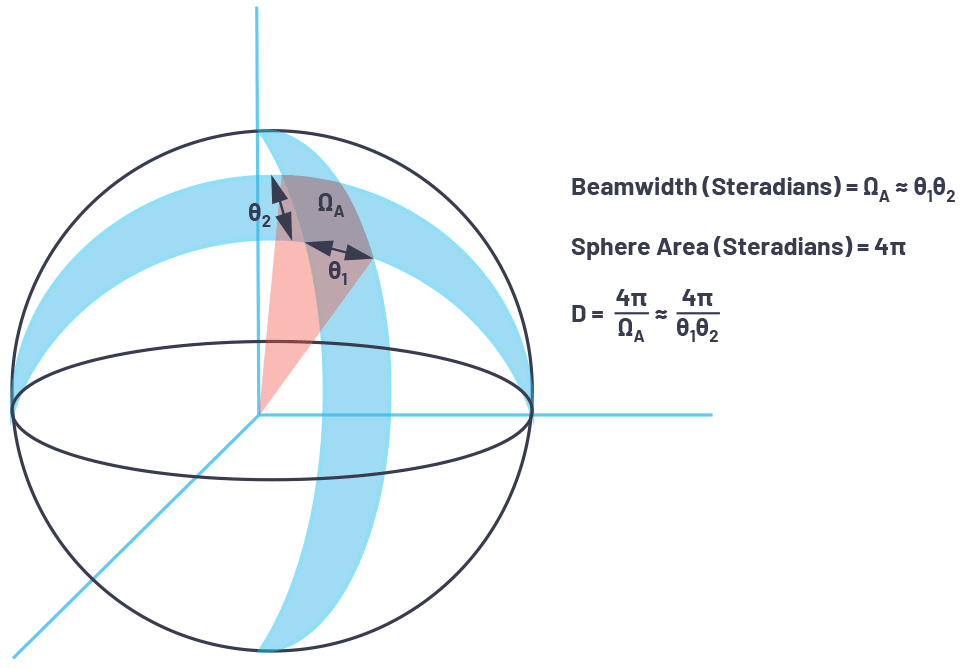
图8.投影到球体上的区域的三维视图。
球体的总表面积为 4π2,并且球体上的面积以球面度为单位定义,球体中的球面度为 4π。因此,各向同性散热器的功率密度为

单位为 (W/m2).
球体的面积有两个角度方向。在雷达系统中,这些通常被称为方位角和仰角。波束宽度可以描述为每个角度方向的函数,如θ1和 θ2:组合在Ω球体上创建一个区域一个.
Ω一个是以球面度为单位的波束宽度,可以近似为 Ω一个≈ θ1× θ2.
识别Ω一个作为球体上的一个区域,方向性可以表示为

我们要考虑的第三个天线术语是孔径。天线孔径代表接收电磁波的有效区域,包括相对于波长的功能。各向同性天线的孔径为

增益相对于各向同性辐射,使天线的有效孔径

将这三个项放在一起,我们可以看到增益可以被认为是定义辐射方向图并考虑天线效率(或损耗)的角度的函数。
线性阵列的数组因子
在这一点上,我们能够预测元件之间的最佳时间(或相位)增量,以实现最大的天线方向性。但我们真的很想了解和操纵完整的天线增益模式。这主要有两个部分。首先,有数组中每个单独元素(可能是一个补丁)的增益,称为元素因子(GE).其次,我们可以通过波束成形阵列施加的影响,称为阵列因子(G一个).全阵列天线增益方向图是两个因素的组合,如公式10所示。

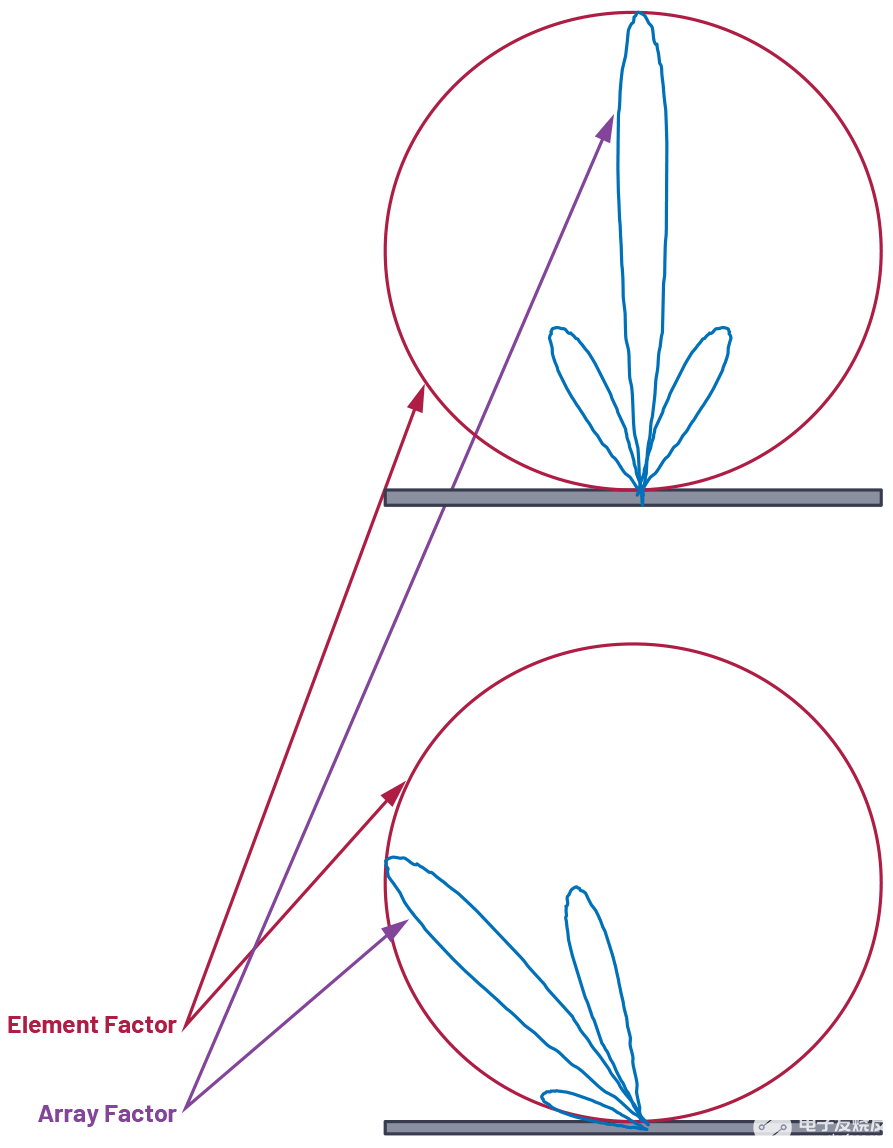
图9.元素和数组因子。
元素因子 GE,是数组中单个元素的辐射模式。这是由天线的几何形状和结构定义的,而不是操作中变化的东西。知道这一点很重要,因为它会限制我们整个阵列的增益,尤其是在地平线附近。但由于我们无法对其进行电控制,因此将其作为总相控阵增益方程的固定影响因素。在本文中,我们假设所有单个元素都具有相同的元素因子。
然后,重点是数组因子 G一个.阵列因子是根据阵列几何形状(d表示我们的均匀线性阵列)和光束权重(振幅和相位)计算的。推导均匀线性阵列的数组因子很简单,但本文末尾引用的参考文献中最好地介绍了细节。
文献中使用的方程存在一些变化,具体取决于线性数组中参数的定义方式。我们使用本文中的公式,这与图 2 和图 3 中的定义保持一致。由于我们主要关注的是增益如何变化,因此绘制相对于单位增益的归一化数组因子通常更具指导意义。该归一化数组因子可以写为公式11。
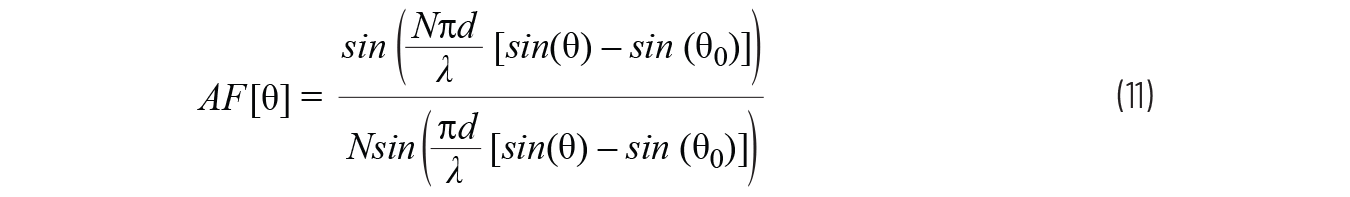
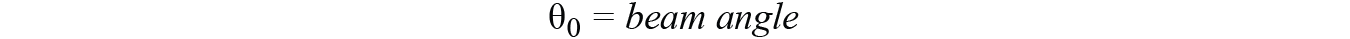
我们已经定义了光束角θ0作为元件之间相移的函数 ΔΦ;因此,我们也可以将归一化天线因子写为公式12。
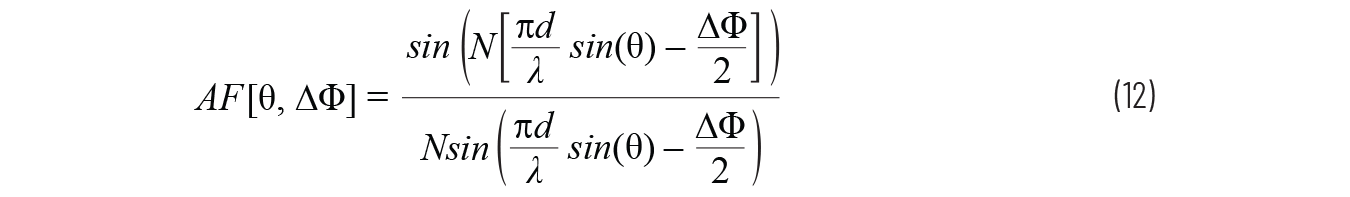
数组因子方程中假设的条件包括:
元素的间距相等。
元素之间存在相等的相移。
这些元素的振幅都相等。
接下来,使用这些方程,我们绘制几种数组大小的数组因子。
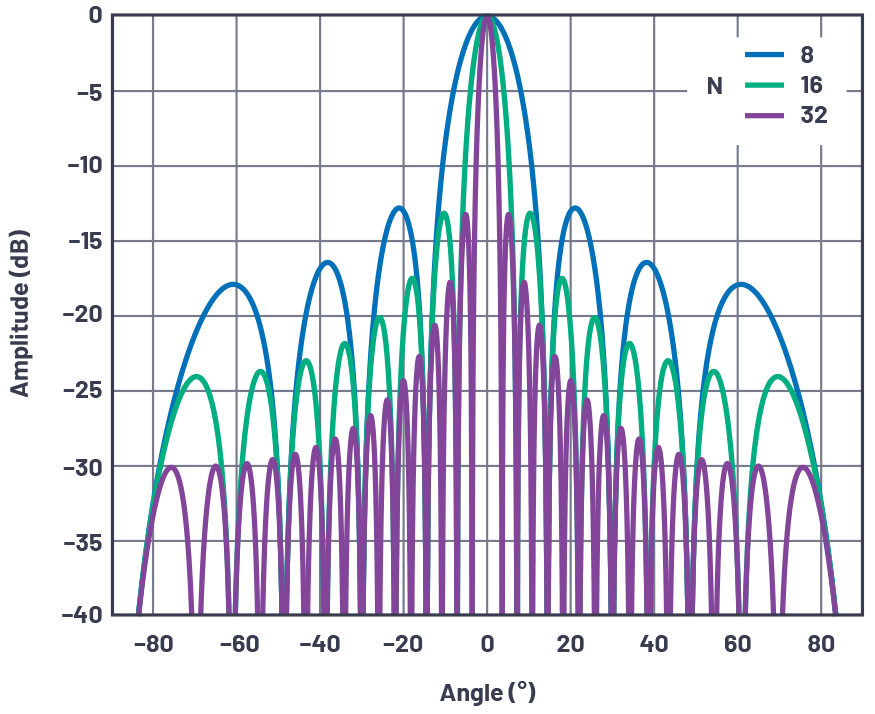
图 10.晶片间距为 d = λ/2 且晶片计数为 8、16 和 32 的线性阵列在视线时的归一化阵列因子。
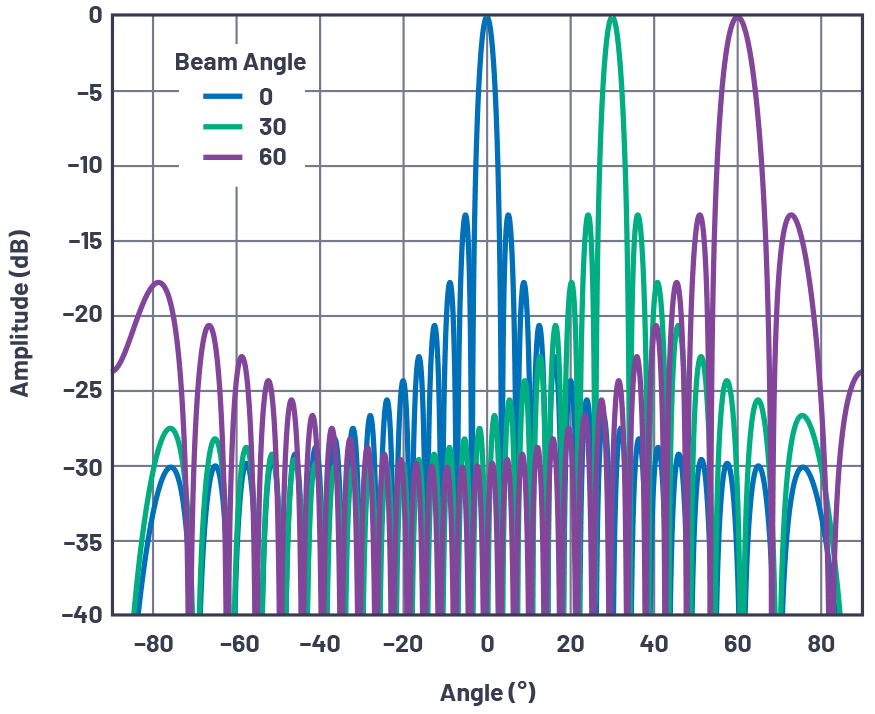
图 11.32 晶片线性阵列在多个波束角下的归一化阵列因子,晶片间距为 d = λ/2。
这些数字的一些观察结果包括:
无论元件数如何,第一个旁瓣的 –13 dBc 都处于 –<> dBc。这是由于数组因子方程中的sinc函数。旁瓣可以通过逐渐减小元件之间的增益来改进,这将是本系列下一节的主题。
波束宽度随着元件数量的增加而减小。
当光束被扫描远离视线时,波束宽度会变宽。
空值的数量随着元素数量的增加而增加。
波束宽度
波束宽度提供了天线角分辨率的指标。最常见的是,波束宽度由半功率波束宽度(HPBW)或主瓣的零点到零点间距(FNBW)定义。为了找到HPBW,我们从峰值向下移动3 dB并测量角距离,如图12所示。
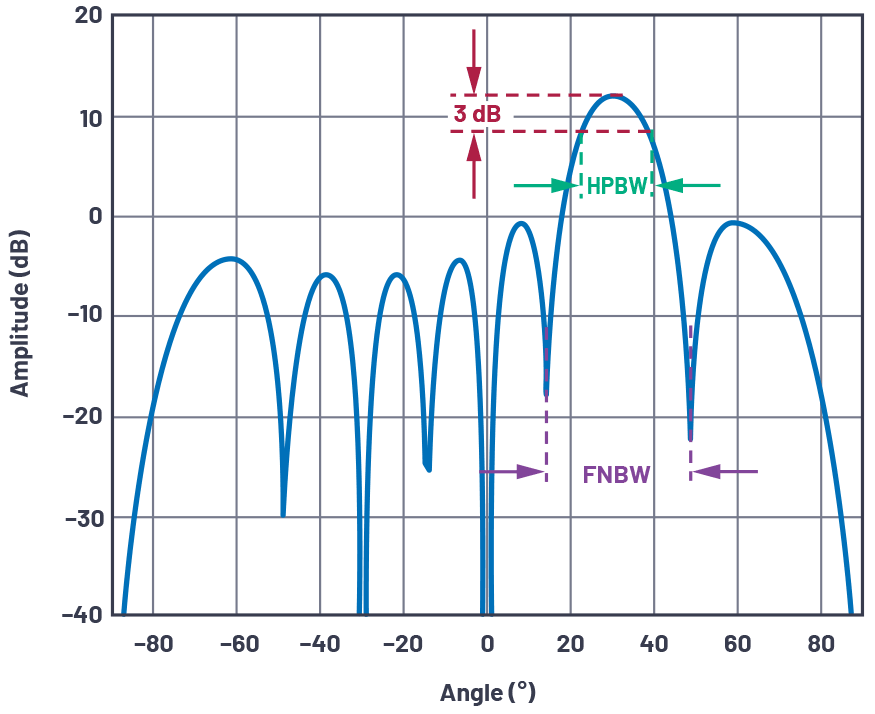
图 12.天线波束宽度的定义(显示的线性阵列N = 8,d = λ/2,θ = 30°)。
使用归一化阵列因子方程,我们可以通过将公式3设置为半功率电平(3 dB或1/√ 2)来求解该HPBW。我们假设机械视孔(θ = 0º),N = 8,d = λ/2。
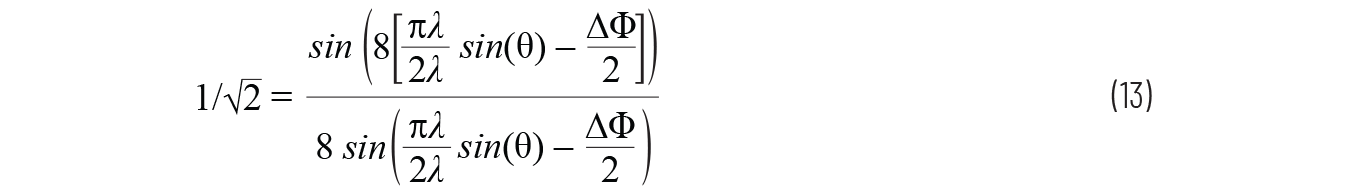
然后求解 ∆Φ 得到 0.35 rad。 使用公式 1,求解 θ:
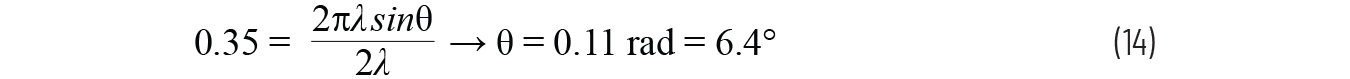
该 θ 是 3 dB 点的峰值,是我们 HPBW 的一半。因此,我们只需将其加倍即可得出 3 dB 点之间的角距离。这导致HPBW为12.8º。
对于等于 0 的数组因子,我们可以重复此操作,并获得前面提到的条件下 FNBW = 28.5º 的第一个零到零间距角。
对于均匀线性阵列,HPBW [1,2] 的近似值为公式 15。

图13绘制了在λ/2晶片间距条件下多个晶片计数的波束宽度与波束角的关系图。
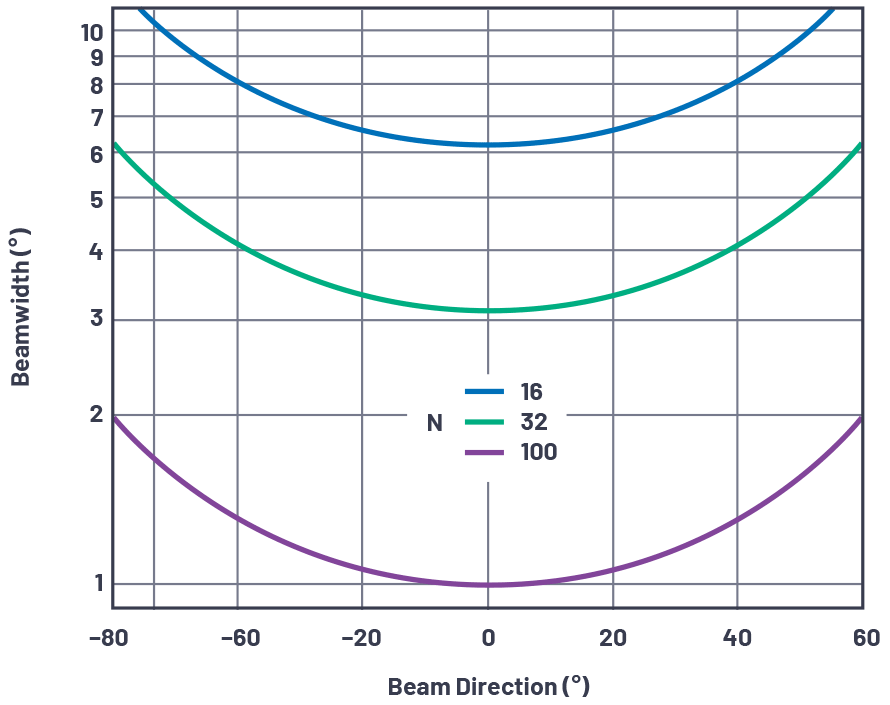
图 13.晶片间距为 λ/2 时的波束宽度与波束角的关系,晶片数量为 16、32 和 100 个晶片。
从此图中,值得注意的是与业界正在开发的阵列大小相关的一些观察结果。
1° 光束精度需要 100 个晶片。如果在方位角和仰角都需要这样做,这将导致 10,000 个元素数组。1°精度仅在接近理想条件下的视线下。在各种扫描角度的现场阵列中保持1°精度将进一步增加晶片数量。然后,该观察结果为具有非常大阵列的波束宽度设定了实际限制。
1000 元素数组在行业中很常见。每个方向的 32 个晶片提供 1024 个晶片计数,并且可以在视线附近产生小于 4° 的光束精度。
可以低成本批量生产的256晶片阵列仍然可以具有小于10°的光束指向精度。对于许多应用来说,这可能是完全可以接受的。
另请注意,对于上述任何一种情况,波束宽度在 60° 偏移时加倍。这是从分母中的 cosθ 开始的,是由于数组的透视缩短;也就是说,从某个角度观察时,阵列看起来是一个较小的横截面。
组合元素和数组因子
上一节仅考虑了数组因子。但是要找到总天线增益,我们还需要元素因子。图 14 演示了一个示例。在这个例子中,我们使用一个简单的余弦形状作为元素因子,或归一化元素增益GE余弦滚降在相控阵分析中很常见,如果考虑平面,可以直观地看到余弦滚降。在宽边,有一个最大面积。当角度远离宽边时,可见区域会根据余弦函数减小。
数组因子,G一个(θ),用于16元素线性阵列,间距为λ/2,辐射图均匀。总模式是元素因子和数组因子的线性乘法,因此在 dB 刻度中,它们可以相加。
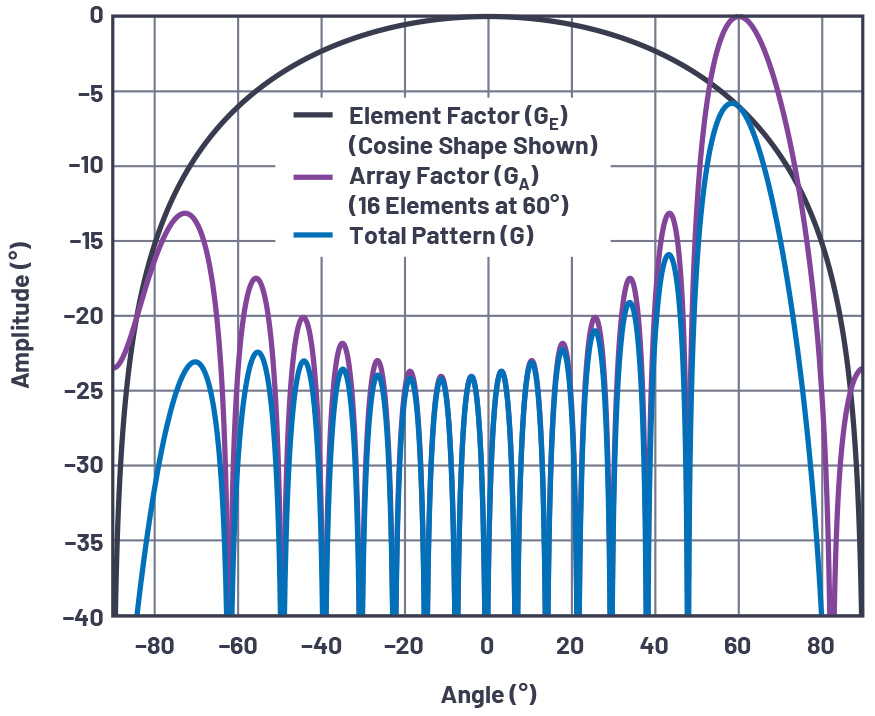
图 14.元素因子和阵列因子组合形成总天线方向图。
光束离开视线时的一些观察结果:
主光束以单元因子的速率失去振幅。
视轴上的旁瓣没有振幅损失。
结果是整个阵列的旁瓣性能从视线下降。
天线图:笛卡尔与极地
到目前为止使用的天线方向图一直在笛卡尔坐标中。但是,在极坐标中绘制天线模式是很常见的,因为它们更能代表从天线向外辐射的空间能量。图 15 是图 12 的重绘版本,但使用了极坐标。请注意,这是完全相同的数据,逐点 - 只是使用极坐标系重新绘制。能够在任一表示中可视化天线方向图是值得的,因为两者都在文献中使用。对于本文的大部分内容,我们将使用笛卡尔坐标,因为在此表示中,比较波束宽度和旁瓣性能可以更容易。
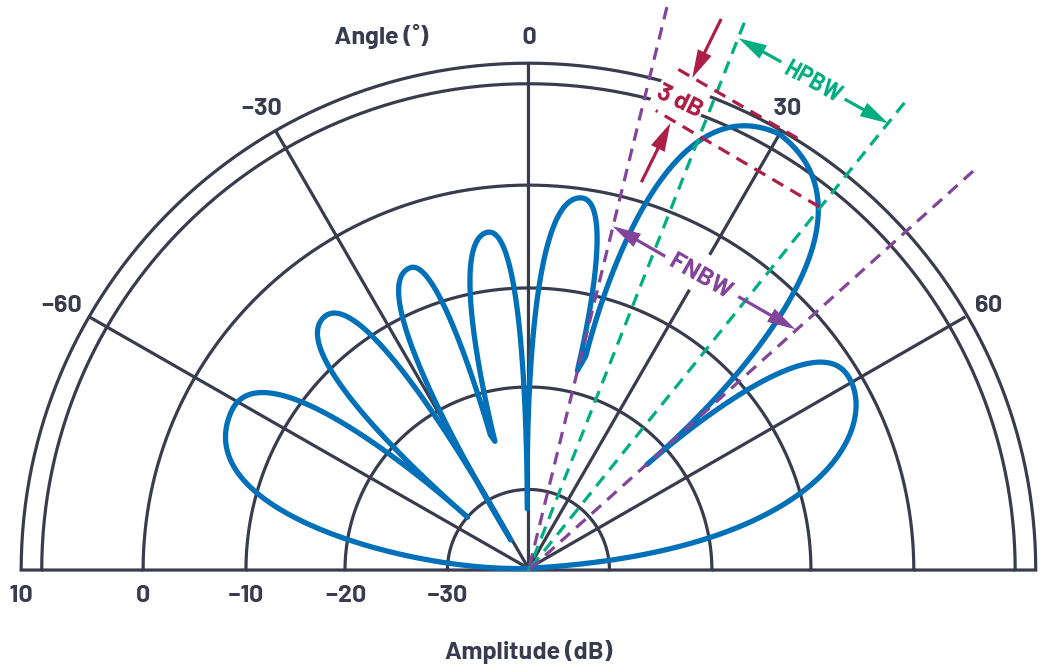
图 15.N = 8、d = λ/2、θ = 30° 的极坐标天线方向性图。
阵列互易性
到目前为止,所有图表和文本都描述了阵列正在接收的信号。但是对于传输阵列来说,这将如何变化呢?幸运的是,大多数天线阵列都是相互的。因此,所有图、方程和术语对于发送和用于接收都是相同的。有时更容易将波束视为被阵列接收。有时,也许在光栅瓣的情况下,您可能会发现将阵列视为传输光束更直观。在本文中,我们通常将数组描述为接收信号。但是,如果这对您来说更难想象,那么您也可以在传输端考虑相同的概念。
总结
本系列的第 1 部分到此结束。介绍了使用相控阵进行波束控制的概念。推导出了用于波束控制的阵列相移的方程,并以图形方式显示。然后,通过观察元件数量、元件间距和波束角如何影响天线响应,定义阵列因子和单元因子。最后,比较了笛卡尔坐标与极坐标中的天线方向图。
本系列即将发表的文章将进一步探讨相控阵天线方向图和损伤。我们将研究天线锥形如何减少旁瓣,光栅瓣如何形成,以及宽带系统中相移与时间延迟的影响。该系列文章最后将分析延迟模块的有限分辨率,以及它如何创建量化旁瓣并降低波束分辨率。
审核编辑:郭婷
-
浅析阵列天线和相控阵2019-06-12 0
-
相控阵天线通道误差对波束形成有什么影响2019-06-13 0
-
机载天线方向图位置优化配置设计2019-07-04 0
-
【模拟对话】相控阵波束成形IC简化天线设计2019-10-01 0
-
图解—相控阵雷达——波束扫描技术2020-05-23 0
-
相控阵天线波束控制的基本原理和波控系统的任务2009-10-06 863
-
16×16多波束相控阵天线的设计2011-06-20 10275
-
HFSS结合UTD计算,分析机载对相控阵天线方向图的影响2019-03-13 2347
-
相控阵天线方向图——锥削对整个阵列的影响2020-12-24 1626
-
相控阵天线方向图:栅瓣和波束斜视2020-12-24 2038
-
相控阵天线原理_相控阵天线设计2021-01-07 10517
-
深入探讨相控阵天线方向图2022-03-14 5913
-
多波束相控阵天线的应用优势2022-05-06 9025
-
相控阵天线方向图的线阵波束特性和阵列因数2022-12-19 3083
-
什么是相控阵天线 相控阵天线波束形成原理2023-07-11 11477
全部0条评论

快来发表一下你的评论吧 !

