

数字成像测量显微镜的放大率误差及校准
描述
测量显微镜是用于测量精密零件的长度和角度的仪器,广泛用于计量室,生产线及科学研究等部门。过去,测量显微镜一般由物镜和测微目镜组成,属于目视仪器的范畴,测量结果容易受到人为因素的影响。在数字成像技术普及以后,测微目镜被CCD相机取代,结合图像分析和数据处理,不但实现了测量自动化,而且提高了测量速度和精度。
测量原理
假设被测零件的长度为y,经物镜成像后的长度为y',物镜的放大倍数为β,那么存在以下关系:

根据几何光学,物镜放大倍数也可以表示为

其中f为物镜物方焦距,f’为像方焦距,且有f’=-f。x为焦物距,即物镜物方焦点到被测物体的距离。x’为焦像距,即物镜像方焦点到像的距离。将(2)代入(1)得到

由(3)可知,当物镜焦距确定后,被测长度值y取决于像的大小y’以及被测物体和CCD表面相对于物镜的位置。如果后者由于某些原因出现偏差,比如CCD安装位置误差或调焦误差(详见下节),就会导致实际放大率偏离理论放大率,从而导致测量误差,因为被测物体的大小是根据公式(1)中的理论放大倍数计算出来的。所谓理论放大倍数是测量显微物镜的主要性能参数之一,通常刻在物镜筒身上,比如1X,0.5X等字样。
物方远心光路
为了保证被测物体清晰地成像在CCD表面,需要改变被测物体到测量显微镜之间的距离,直到得到清晰的像为止,这个过程称为调焦。
调焦可以有手动调焦和自动调焦,但不管采用哪种方式都存在调焦误差。见图1,红色实线表示正确的物像位置,蓝色实线表示存在调焦误差时的情形。对于普通显微物镜来说,蓝色光束的主光线(通过孔径光阑中心的光线,代表光束中心)的方向相对于红色光束的主光线发生了改变,和CCD表面的交点由A’跑到了B’,也就是说测得的像的大小发生了改变,实际放大率不等于理论放大率,从而造成了测量误差。
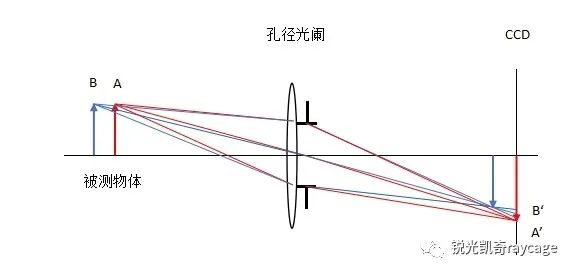
图1. 普通物镜
采用物方远心光路能够消除调焦误差引起的测量误差。见图2,孔径光阑放置在物镜像方焦平面上,入瞳在物方无穷远,物方主光线始终与光轴平行。无论被测物体位置如何改变,出射光束的主光线方向始终不变。即使存在调焦误差,CCD上的像仅改变清晰度,而不改变大小。因此物方远心光路不产生放大率误差引起的测量误差。当然,由于光阑外移,轴外像差变大,物镜的结构趋于复杂,价格远高于普通物镜。
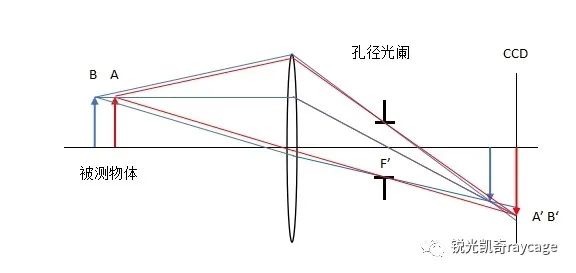
图2. 物方远心光路
测量显微镜的校准
虽然物方远心光路能够消除调焦误差带来的测量误差,但是CCD位置误差仍然会引起测量误差,因此测量显微镜使用之前必须经过校准。通常用直尺作为标,如图3所示,首先测量出直尺像的某段长度(比如从-5mm—5mm)所占据的CCD像素的个数,乘以像素的大小,再除以物镜的理论放大率,便得到了直尺的某段长度的测量值。
该测量值应该等于10mm,但是由于CCD位置误差,测量值往往不等于10mm,比如可能是10.1mm。多余的0.1mm就是系统误差,以后每次测量结果都要减去 0.1mm。或者调整CCD的位置后再次进行校准,直到测量值等于或接近10mm。
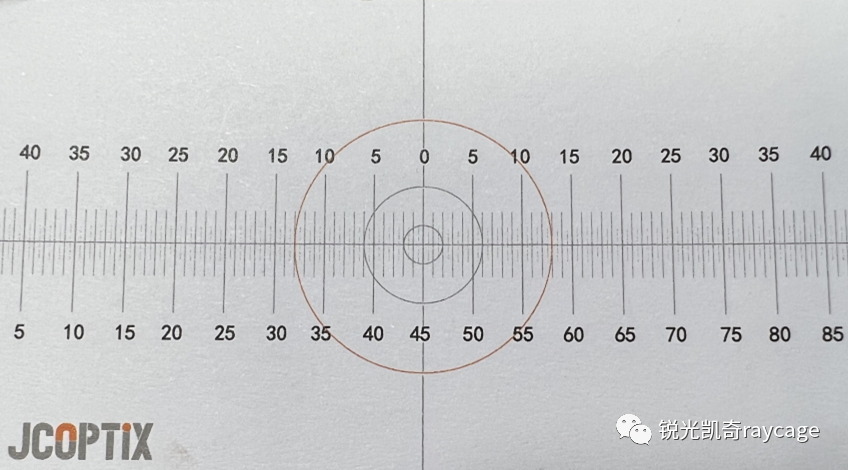
图3. 校准分划板,1“ X 1”,格值100µm。
由于直尺的刻线有一定宽度,其像的宽度往往大于一个CCD像素,在确定两条刻线之间的CCD像素的个数时往往受到人为因素的影响,从而造成偶然误差。为此我们采用图4所示的标准图案来代替直尺进行校准,其优点是借助MATLAB图像处理工具包自动识别图形并计算出图案的大小,避免了人为因素的影响。已知标准图案为4x4mm的黑白正方形,测量使用的是Edmund 0.9X CobaltTL 远心镜头(产品号 62901),记录使用的是AVT CCD的相机,像素大小为5.5x5.5µm,测试过程的细节参考视频1:
视频1 测试细节
使用视频1的系统的相机拍摄的图像如图5所示。然后对图5进行计算机图像处理,用MATLAB编写的程序代码见附录。程序第一段是读入图像并显示。第二段是将灰度图像转换成如图6所示的二值(黑白)图像。第三段第一行的函数regionprops() 对每个白色区域的面积,重心和边界框进行统计,统计结果见图7。其中面积以像素的个数来表示,重心以x,y坐标表示,边界框用4个数值表示,第一,二个数值是矩形左上角的x,y坐标,第三,四个数值分别是矩形的宽度和高度,以像素的个数表示。
然后给每个白色区域打上标签,如图8所示,可见一共有10个白色区域。容易看出只有4,5,7三个矩形是完整的,因此第四段第一句是筛选出这三个矩形,其余矩形不予考虑。第二句是提取这三个矩形的边界框的数据,并将它们写入二维数组BoundingBoxes。从图7可以看出,第4,5,7三个矩形的宽度和高度均等于660个像素。最后一句是计算3个正方形边长的平均值,为660个像素,乘以CCD像素大小0.0055mm,再除以理论放大率0.9,得到正方形边长的测量值为4.033mm,比标准值大了0.033mm。在以后的测量中,需要将测量值减去0.033mm。
图4. 标准图案

图5. 标准图案的原始图像

图6. 二值图像
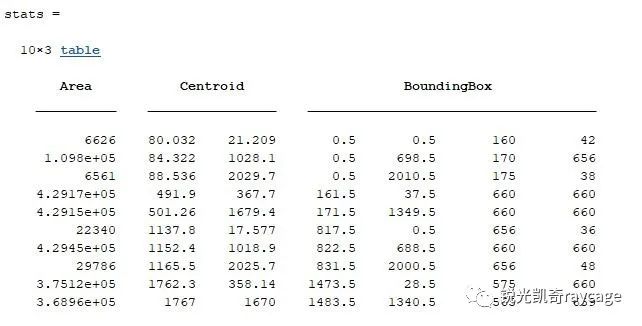
图7. 10个白色区域的面积,重心,边界框数据列表

图8. 打了标签的原图
结语
本文介绍了测量显微镜的工作原理及测量误差的主要来源─放大率误差,而放大率误差主要来自于调焦误差和CCD表面相对于物镜的位置误差。采用物方远心光路,即将孔径光阑置于物镜像方焦平面上能够有效地消除调焦误差导致的测量误差。用直尺或标准图案进行放大率校准则能够测出实际放大率和理论放大率之间的偏差,用以补偿CCD位置误差造成的测量误差。本文介绍了如何用标准图案和MATLAB强大的图像处理工具包测量实际放大率,并分享了程序代码。
附录:MATLAB图像处理程序代码
beta = 0.9; % magnification
px = 0.0055; % CCD pixel size (mm)
I=imread('checkerboard.bmp','bmp');
figure(1)
imshow(I)
title('Original image')
bw = imbinarize(I,0.3);
figure(2)
imshow(bw)
title('Binary image')
stats = regionprops('table',bw,'Area','Centroid','BoundingBox')
n = size(stats,1);
centroids = cat(1,stats.Centroid);
position = round(centroids);
RGB = insertText(I,position,1:n,'FontSize',50,'AnchorPoint','Center');
figure(3)
imshow(RGB)
title('Labelled image')
% filter out smaller boxes
idx = find([stats.Area] > 400000);
% extract the data for the square boxes
boundingBoxes = cat(1,stats(idx,:).BoundingBox);
% calculate the size of the square boxes
mean(mean(boundingBoxes(:,3:4)))*px/beta
审核编辑:刘清
-
立体显微镜—上海应捷2009-07-07 0
-
体视显微镜—上海应捷2009-07-07 0
-
金属焊接溶深测量检测技术-显微镜检测技术2011-04-01 0
-
金属焊接溶深焊缝测量检测技术-显微镜检测技术2011-04-11 0
-
选购显微镜的一些常见问题2016-08-31 0
-
Cyclops Micro高清数字显微镜2018-10-31 0
-
显微镜的成像原理图2019-07-24 0
-
显微镜倍率如何计算?2020-02-06 0
-
如何计算显微镜的放大倍数2020-02-11 0
-
显微镜分析经验---放大倍率计算2020-03-23 0
-
显微镜放大倍数是怎么得出来的?2020-04-26 0
-
为什么激光共聚焦显微镜成像质量更好?2023-08-22 0
-
显微镜成像原理图2009-11-18 17863
-
显微成像与精密测量:共聚焦、光学显微镜与测量显微镜的区分2024-05-11 886
-
共聚焦、光学显微镜与测量显微镜的区分2024-05-14 435
全部0条评论

快来发表一下你的评论吧 !

