

混叠频率计算器
描述
本应用笔记提供一种快速、容易使用的工具,用来确定镜像信号的真实位置和重叠频率的位置,以及典型频谱中的谐波频率。所得数据用于分析模/数转换器(ADC)和数/模转换器(DAC)的动态特性。
这个基于Excel®、简单易用的重叠频率计算器提供了一种在数据采样系统的第一奈奎斯特频带中定位基波谐波的快速方法。此计算器与采样过程无关,系统可以工作在奈奎斯特采样、过采样或欠采样。这个工具对于确定ADC、DAC在第一奈奎斯特频带中的重叠频谱非常有用。
本应用笔记讨论了计算第一奈奎斯特频带中混叠频率的方法,包括重叠频率计算器的详细使用说明。另外,为了增进理解,文中简要讨论了数据采样系统或特定数据转换器中混叠频率和奈奎斯特频率的概念。
混叠频率和奈奎斯特频率
众所周知,数据采样系统中存在频率混叠现象,当一个信号以低于奈奎斯特频率的时钟采样时将会发生频率混叠,这里的奈奎斯特频率是2倍的信号频带带宽。现实世界中的信号频谱都包含基波谐波,以及频带内、外的噪声。系统固有的非线性和采样过程的非线性会在输出波形中产生基波的谐波成分。所有高于fSAMP/2的高次谐波,fSAMP为采样频率,混叠频率将会进入第一奈奎斯特频带(图1a、1b)。
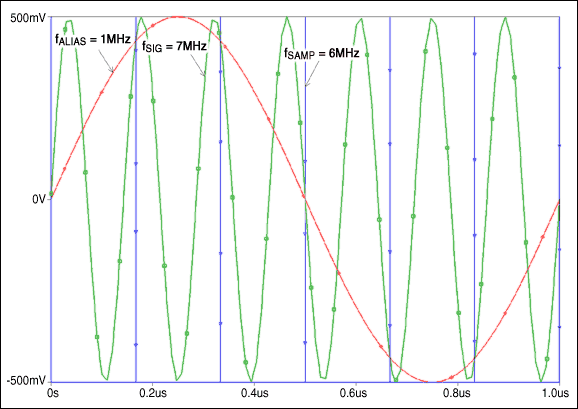
图1a. 时域中的混叠现象
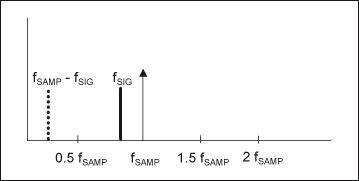
图1b. 频域中的混叠现象
离散时域信号的快速傅立叶变换(FFT)频谱可以划分到无穷多个fSAMP/2频带,即奈奎斯特频带。DC与fSAMP/2之间的频谱是第一奈奎斯特频带。频谱分量在不同的奈奎斯特频带重复。注意:偶次奈奎斯特频带是奇次奈奎斯特频带的镜像(图2)。
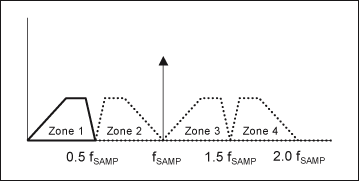
图2. 多个奈奎斯特频带示意图
ADC与DAC的频率混叠
ADC中的混叠是由输入级模拟信号的采样/保持(T/H)过程产生的。在数字信号处理(DSP)领域,T/H过程等于脉冲序列(由采样时钟确定)的频谱与模拟输入频谱的卷积。卷积结果产生了不同奈奎斯特频带中的周期性频谱。当输入信号包含有大于奈奎斯特频率(fSAMP/2)的频谱成分时,相邻奈奎斯特频带将产生相互重叠,从而产生频率混叠现象。
DAC中的混叠是由输出级离散时间采样的零阶保持(ZOH)过程产生的(零阶保持器用于避免码相关的脉冲干扰)。在DSP领域的零阶保持过程等于sin(x)/x频谱(表现为矩形函数,用于保持离散时间样本)与DAC核输出脉冲序列频谱(振幅变化)的卷积。另外,与ADC一样,不同奈奎斯特频带的周期性输出频谱是卷积的结果。
计算器
从数学角度看,如果没有频率混叠,所有低于fSAMP/2的频率成分都将出现在频谱中。然而,由于频率混叠,任何高于fSAMP/2的谐波成分(fHARM)也会作为镜频出现,频率为:|± K x fSAMP ± fHARM |,其中K = 1, 2, 3, 等。
以下运算用于计算第一奈奎斯特频带中的不同谐波:
fNYQ = fSAMP/2; fHARM = N x fFUND; //N is an integer If (fHARM lies in an odd Nyquist zone) then fLOC = fHARM % fFUND; //% is the modulus operator else fLOC = fFUND - (fHARM % fFUND); End;
其中,fNYQ为奈奎斯特频率,fSAMP为采样频率,fFUND为信号基频,fHARM为信号谐波频率,fLOC为谐波分量在第一奈奎斯特频带中的位置。
使用简单的电子计算器求取不同谐波频率(fHARM)的位置(fLOC),首先必须确定迭代次数。
重叠频率计算器运算时需要两个输入变量:采样频率fSAMP和信号基频fFUND。通过这两个变量,该计算器可以求出奈奎斯特频率(fNYQ),不同谐波频率的绝对值(fHARM),以及重叠频谱中第一奈奎斯特频带的不同谐波。表1给出了一个计算重叠频率的例子。
| N | fNYQ (MHZ) | fHARM (MHz) | fLOC (MHz) |
| 1 | 250.000000 | 29.96826172 | 29.96826172 |
| 2 | 59.93652344 | 59.93652344 | |
| 3 | 89.90478515 | 89.90478515 | |
| 4 | 119.8730469 | 119.8730469 | |
| 5 | 149.8413086 | 149.8413086 | |
| 6 | 179.8095703 | 179.8095703 | |
| 7 | 209.777832 | 209.777832 | |
| 8 | 239.7460937 | 239.7460937 | |
| 9 | 269.7143555 | 230.2856445 | |
| 10 | 299.6826172 | 200.3173828 | |
| 11 | 329.6508789 | 170.3491211 | |
| 12 | 359.6191406 | 140.3808594 | |
| 13 | 389.5874023 | 110.4125977 | |
| 14 | 419.5556641 | 80.44433595 | |
| 15 | 449.5239258 | 50.47607423 |
审核编辑:郭婷
-
内存异步频率计算器2008-10-30 0
-
LC谐振威廉希尔官方网站 频率计算工具2007-06-05 10755
-
RC振荡威廉希尔官方网站 频率计算器工具2008-10-30 19677
-
lcrc谐振频率计算器2008-10-30 2969
-
频率计算器2008-10-30 1624
-
LC谐振频率计算器 (工具软件)V1.202009-03-20 3272
-
混叠频率计算器2009-04-16 1762
-
DS1090频率计算器2009-04-21 625
-
基于DS1090的频率计算器2009-12-14 799
-
LC谐振频率计算器2016-05-05 2216
-
用于计算第一奈奎斯特区折叠频率位置的折叠频率计算器2023-02-07 3318
-
DS1086L的频率计算器2023-06-12 818
全部0条评论

快来发表一下你的评论吧 !

