

在 MATLAB 中实现层次分析法的主要步骤
描述
层次分析法原理
层次分析法(Analytic Hierarchy Process,AHP)是一种多准则决策分析方法,可用于辅助决策者在多个指标或因素中进行排序或比较。该方法可以通过对多个因素进行两两比较获得权重,从而建立一个层次结构,进而进行综合评价和排名。
下面是一些详解层次分析算法的步骤:
明确决策目标,确定需要评估的准则和子准则:首先明确决策目标,然后考虑需要评价的准则和子准则。这些准则和子准则应该尽可能具体、完整,以便进行比较。
建立层次结构:将目标、准则和子准则构成一个层次结构,其中目标位于最顶层,准则和子准则逐层展开,直到最底层。
对每个准则和子准则进行两两比较,得出权重:对于每个准则和子准则,根据它们对上一级准则或目标的相对重要性进行两两比较,生成判断矩阵,并计算出每个准则和子准则相对于上一级准则或目标的权重。
计算一致性比率(CR):在计算权重时,需要考虑判断矩阵的一致性。通过计算一致性指标和随机一致性指标,可以得出一致性比率,并判断结果是否可行。
综合评价:根据各个准则和子准则的权重,可以得出每个方案的综合评价。
层次分析法是一种较为常用的决策分析方法,应用广泛。但是,在实际应用中需要注意判断矩阵的构造和一致性比率的计算,以确保评价结果的可靠性。
层次分析法数学模型
层次分析法 (Analytic Hierarchy Process, AHP) 包含的数学公式如下:
相对重要性矩阵
将两两比较得出的判断矩阵记为 ,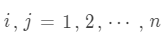 。其中, 表示因素 相对于因素 的相对重要度。
。其中, 表示因素 相对于因素 的相对重要度。
加权矩阵
将相对重要性矩阵 与准则/子准则的权重向量 相乘,得到加权矩阵 :
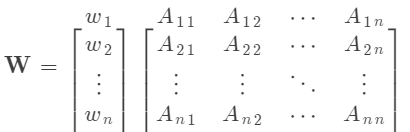
一致性指标
通过计算加权矩阵 的列和,得到一致性指标 :
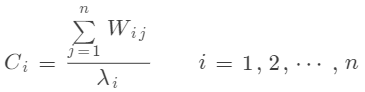
其中, 是与 相关的最大特征根。
随机一致性指标
在 的范围内,预先计算一组随机一致性指标 ,然后计算随机一致性比例 :
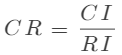
其中,CI 是一致性指标。
最终权重向量
当 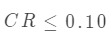 时,可将 当作最终权重向量。最终权重向量 可以通过归一化加权矩阵得到:
时,可将 当作最终权重向量。最终权重向量 可以通过归一化加权矩阵得到:
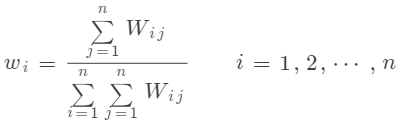
以上就是层次分析法中的主要数学公式。在具体应用中,需要进行矩阵运算、特征根分解等数学操作。
MATLAB代码实现
在 MATLAB 中实现层次分析法可以参考以下步骤:
构造相对重要性矩阵
通过两两比较,构造相对重要性矩阵 。在 MATLAB 中,可以使用 inputdlg() 函数获取用户输入的相对权重值,再根据这些值构造相对重要性矩阵。
例如,假设需要评估三个因素 A、B 和 C 的相对重要性,可以使用如下代码创建相对重要性矩阵:
% 获取用户输入的相对权重值
prompt = {'A 相对于 B 的重要性:', 'A 相对于 C 的重要性:', 'B 相对于 C 的重要性:'};
name = '输入相对重要性';
numlines = 1;
defaultans = {'', '', ''};
answer = inputdlg(prompt, name, numlines, defaultans);
% 构造相对重要性矩阵
A = [1 str2double(answer{1}) str2double(answer{2});
1/str2double(answer{1}) 1 str2double(answer{3});
1/str2double(answer{2}) 1/str2double(answer{3}) 1];
计算权重向量
计算准则/子准则的权重向量 ,可以用 eig() 函数计算相对重要性矩阵 的特征向量和特征值,再将特征向量进行归一化。
例如,使用如下代码计算权重向量:
% 计算特征向量和特征值 [eigvec, eigval] = eig(A); % 获取最大特征值的索引 [~, max_eigval_index] = max(diag(eigval)); % 获取对应的特征向量,并进行归一化 w = eigvec(:, max_eigval_index); w = w / sum(w);
检验一致性
计算一致性指标 和随机一致性比例 ,判断评价结果的可靠性。通常,当 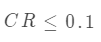 时,可以认为评价结果可靠。
时,可以认为评价结果可靠。
例如,使用如下代码进行一致性检验:
% 计算一致性指标 CI = (max(diag(eigval)) - 3) / (n - 1); % 预先计算随机一致性比例 RI = [0 0 0.58 0.9 1.12 1.24 1.32 1.41 1.45 1.51]; % 计算随机一致性比例 CR = CI / RI(n);
输出结果
输出准则/子准则的权重向量和一致性检验结果。例如,使用如下代码输出结果:
% 输出权重向量
for i = 1:n
fprintf('%s 的权重:%.4f
', criteria{i}, w(i));
end
% 输出一致性检验结果
fprintf('一致性指标 CI = %.4f,随机一致性比例 CR = %.4f
', CI, CR);
if CR <= 0.1
fprintf('一致性检验通过,评价结果可靠。
');
else
fprintf('一致性检验未通过,评价结果不可靠。
');
end
以上就是在 MATLAB 中实现层次分析法的主要步骤。需要注意的是,层次分析法的实现过程中需要进行矩阵运算和特征值计算等较为复杂的操作,建议使用函数封装实现。
责任编辑:彭菁
-
层次分析法.pdf2009-09-15 0
-
基于灰色层次分析法的战场电磁环境效应评估2010-05-04 0
-
基于matlab对在轴承故障声学检测小波分析法代码2015-07-06 0
-
层次分析法的应用与实现2019-06-03 0
-
层次分析法是什么2021-07-19 0
-
层次分析法2009-09-15 707
-
层次分析法及其在电力系统中的应用2010-08-14 426
-
层次分析法的改进及应用2011-08-15 747
-
Matlab-层次分析法2015-12-08 454
-
算法大全_层次分析法2016-01-14 559
-
基于层次分析法的电网应急演练管理系统研究与实现2017-11-16 780
-
基于模糊层次分析法的安全态势评估中2017-11-24 1125
-
基于层次分析法的通信指挥效能评估方法2018-01-13 758
-
基于熵值模糊层次分析法的科学评价体系2021-06-21 561
-
基于层次分析法的输电线路防山火预警评估模型.论文2021-11-24 727
全部0条评论

快来发表一下你的评论吧 !

