使用信赖域法求解无约束优化问题

使用信赖域法求解无约束优化问题

在 MATLAB 中，可以使用 fminunc 函数来求解无约束优化问题，其中包括信赖域法。fminunc 函数的使用方法非常灵活，可以通过修改参数来指定不同的算法、梯度计算方法等。

以下是一个使用信赖域法求解无约束优化问题的简单示例：

假设有以下无约束优化问题：

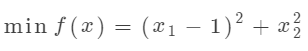
下面是 MATLAB 的代码实现：

% 定义目标函数和梯度函数
f = @(x) (x(1)-1)^2 + x(2)^2;
grad_f = @(x) [2*(x(1)-1); 2*x(2)];

% 定义初始点和参数
x0 = [0; 0];
options = optimoptions('fminunc','Display','iter','Algorithm','trust-region');

% 调用fminunc函数进行优化
[x,fval,eflag,output,grad,hessian] = fminunc(f,x0,options);

在上面的代码中，首先定义了目标函数 f 和梯度函数 grad_f，然后调用 fminunc 函数来求解优化问题。需要注意的是，信赖域法需要计算 Hessian 矩阵，因此需要将 fminunc 函数的输出参数中的 Hessian 矩阵 hessian 提取出来。如果不需要计算 Hessian 矩阵，可以通过将 fminunc 函数的参数 'Hessian','off' 来禁用 Hessian 计算。

信赖域法还有一些其他的参数可以调整，例如信赖域半径、最大迭代次数、收敛容限等。我们可以通过修改 options 结构体中的参数来指定不同的值。在上面的代码中，我们指定了 Algorithm 为 'trust-region'，即使用信赖域法求解无约束优化问题，默认情况下 fminunc 函数使用拟牛顿法进行优化。

需要注意的是，信赖域法需要计算目标函数的梯度，因此要确保梯度函数的正确性。如果没有提供梯度函数，则 fminunc 函数会通过自动微分方法计算梯度。

　　审核编辑：汤梓红