

Ansys Maxwell&optiSLang电机时空二维电磁力谐波优化设计案例
电子说
描述
1 电机电磁力的基本概念
电机运行时,其内部有三类电磁力存在,分别是麦克斯韦张力、洛伦兹力及磁致伸缩力。导致电机电磁振动的主要因素是铁心受到的麦克斯韦张力,且定子受到的电磁力绝大部分作用于定子齿尖。为便于分析,一般将电磁力分解为径向电磁力和切向电磁力,径向电磁力比切向电磁力的分量大很多,径向电磁力经齿传递到轭部,引起定子轭部径向的形变。切向电磁力导致转矩波动,引起齿部切向形变,将引起轴系共振。
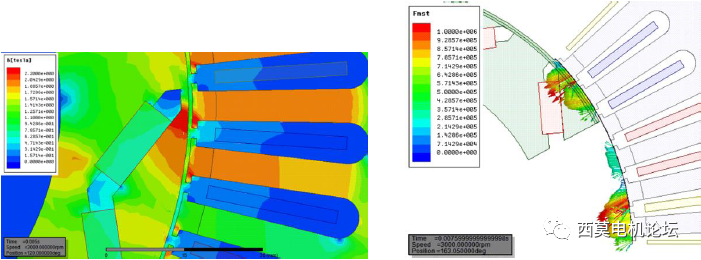
径向电磁力
其中,Maxwell应力张量法表达式如下。
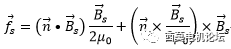
径向电磁力及切向电磁力表达式如下,其单位均为N/m2。
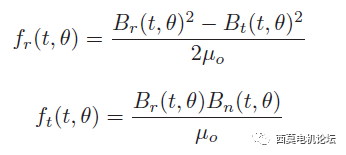
在Maxwell中,通过场计算器添加径向电磁力Br及切向电磁力Bt可按如下操作进行。
添加Br
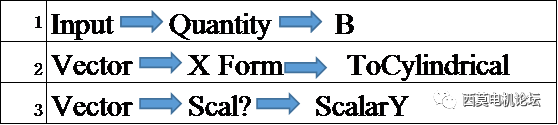
添加Bt
径向及切向电磁力密度表达式如下。
径向电磁力:(Br^2-Bt^2)/Mu0/2
切向电磁力:(Br*Bt)/Mu0
最终,在Maxwell中生成如下所示的径向及切向电磁力表达式。
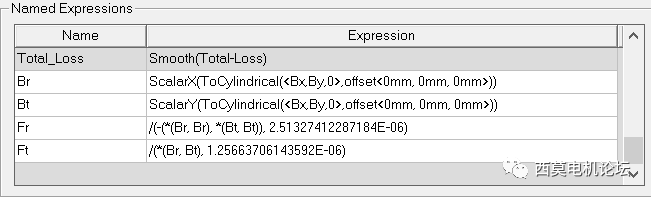
径向及切向电磁力表达式
利用Maxwell瞬态场仿真得到定子齿部某点电磁力随时间变化的结果,通常,时域下的电磁力难以获得足够的信息,因此,我们需要将电磁力从时域变换到频域,即一维傅里叶变换。利用离散傅里叶变换(DFT),将随时间变化的波形转换到频域,得到各次频率谐波的幅值及相位,这种时域到频域的转换,便于对复杂电磁力波的分析与优化,并应用于结构谐响应分析。
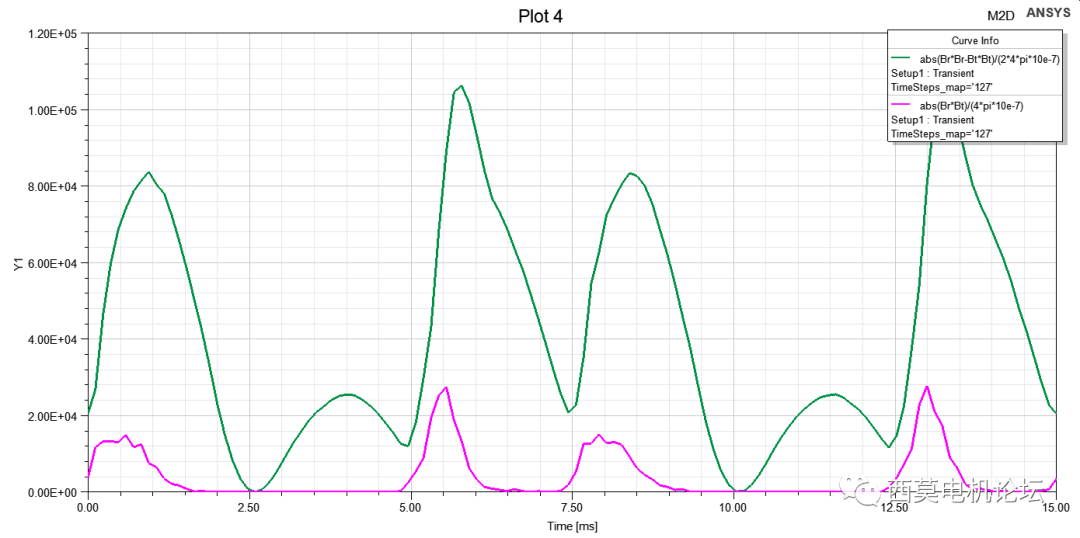
时域电磁力
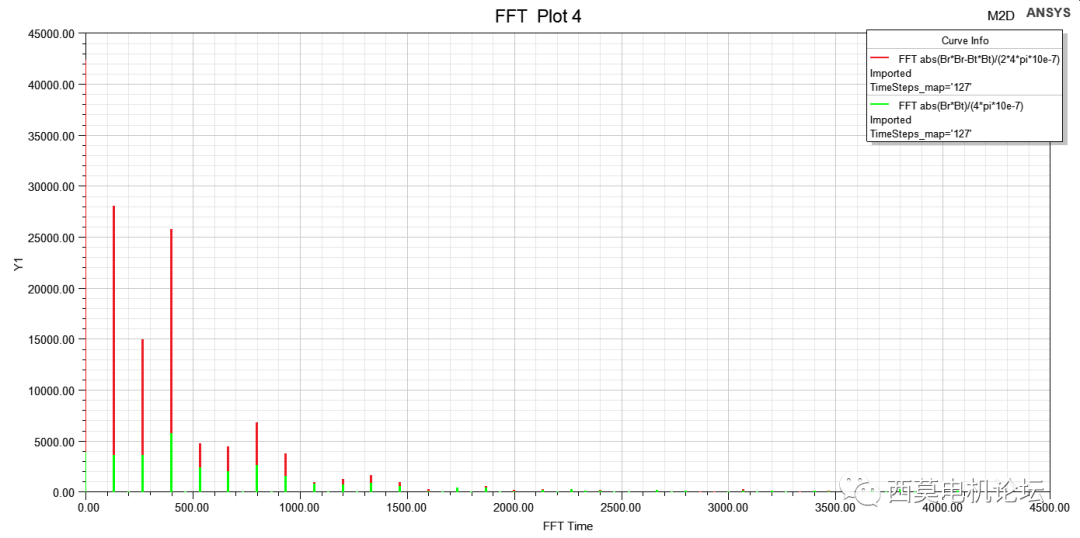
频域电磁力
转子旋转运动时,从整个气隙圆周上看,电磁力同时具有时间和空间属性。电磁力在时域下看似杂乱无序,但从其产生根源分析,它可以看成由无数个具有不同幅值、空间阶数、时间阶数的旋转运动的行波叠加而成。
径向电磁力可分解为如下表达式。
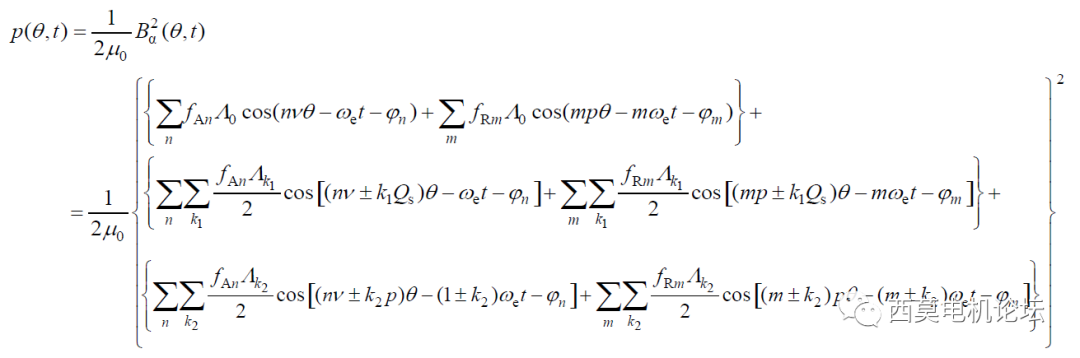
在这些无穷尽的谐波分量中,有一些分量对电机NVH有较大的影响。如空间阶数 <= 4 且其幅值较大时,亦或是空间阶数和(或)频率(时间阶数)与定子铁心的固有振型及固有频率接近或相等时,当这些情况发生时,电机将会产生较大的噪音,影响电机声品质结果。
因此,如果我们可以提取出这些关键的时、空电磁力谐波分量,并将其作为优化目标,那么电机NVH的优化流程无需进行结构谐响应分析,优化设计效率将大幅提高。因此,我们可以通过二维傅里叶变换(Two-Dimensional FourierTransform(2DFFT))来对这些谐波含量进行提取,然后有针对性的对其进行优化降低。

二维傅里叶变换(Two-Dimensional Fourier Transform(2DFFT))
在2022R2版本之前,Maxwell无法直接进行FFT2D,因此我们开发了用于FFT2D的UDO脚本,可实现用户指定的任意时、空阶次幅值的输出,同时支持导出所有FFT2D结果矩阵到csv文件,利用该脚本即可实现对电磁力某时、空阶次幅值的优化。
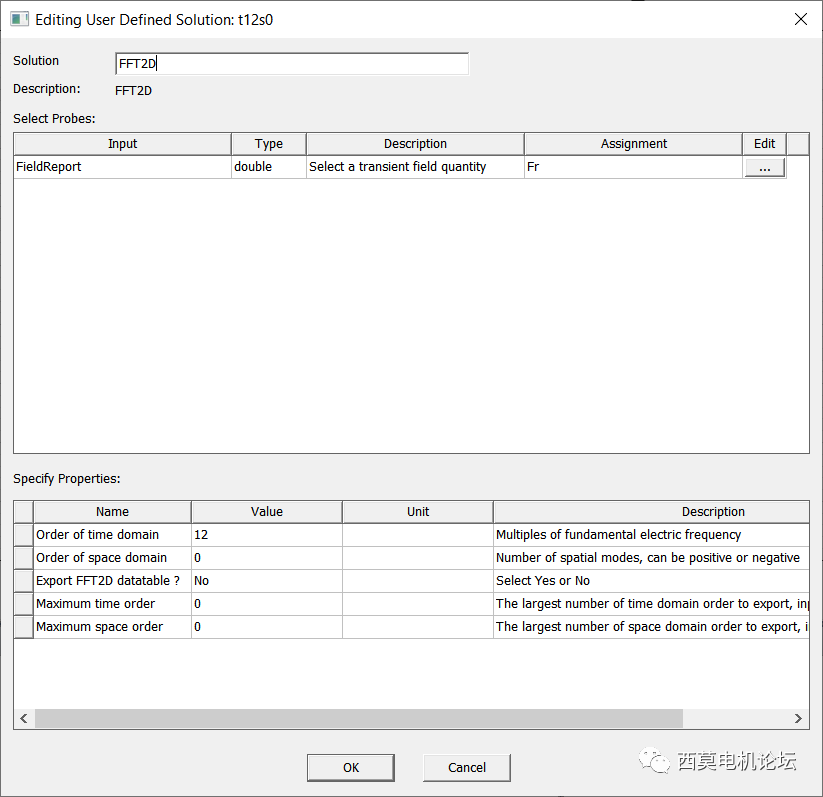
FFT2D脚本
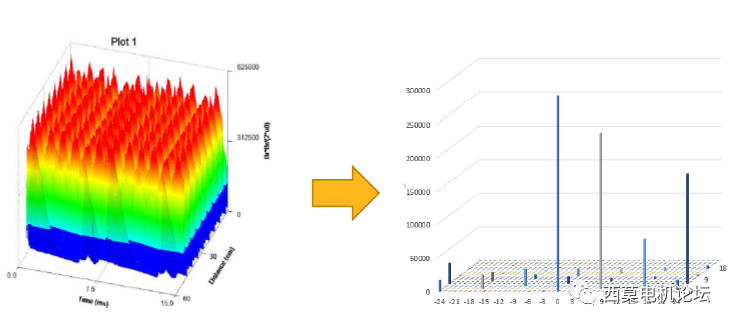
导出所有FFT2D结果矩阵到csv文件并图标显示结果
Maxwell 2022R2新增电磁力二维傅里叶变换功能,用户可直接在软件中进行电磁力二维傅里叶变换,无需借助脚本。
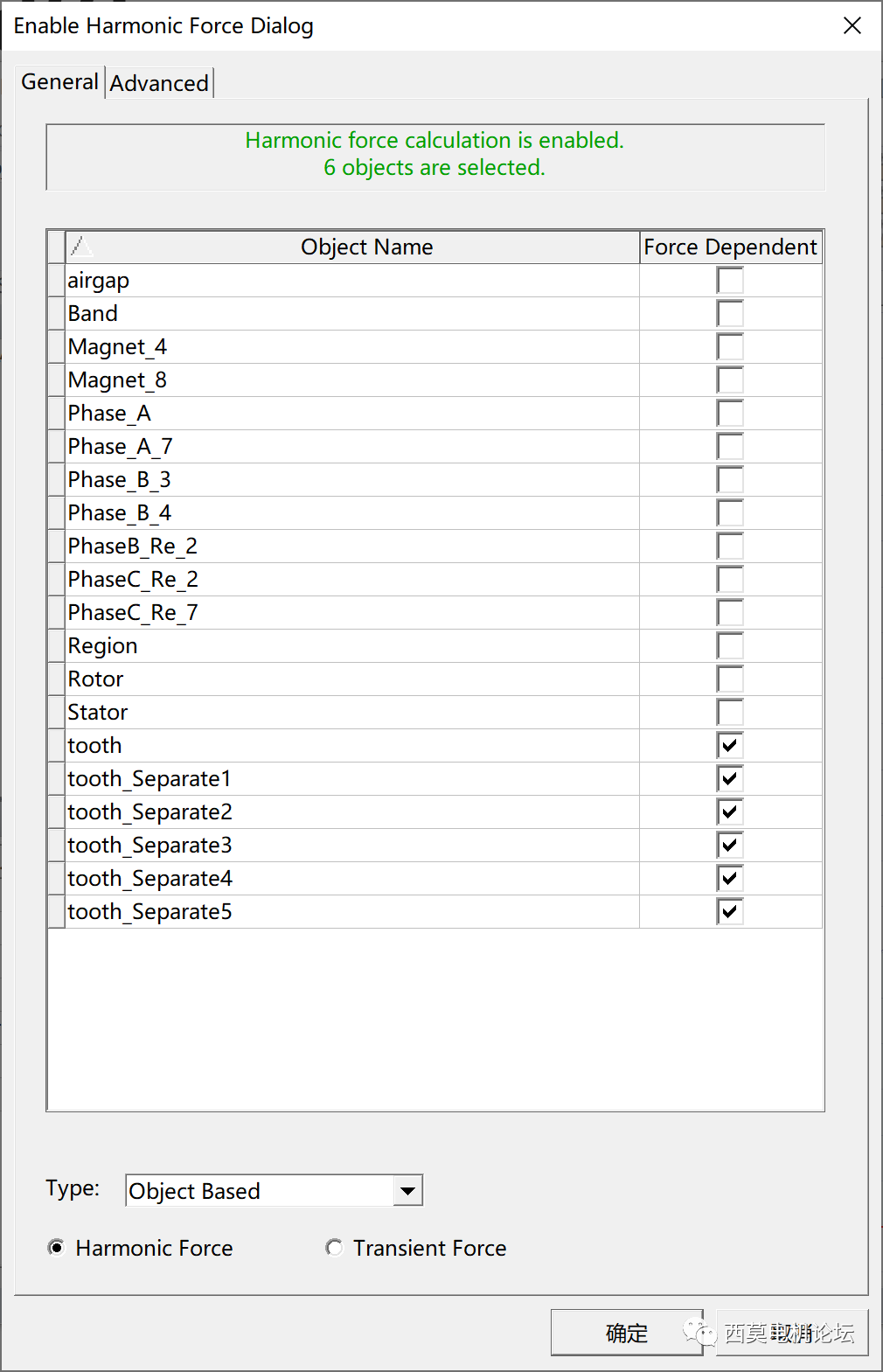
首先进行object Based谐波电磁力计算
Maxwell 2022R2新增电磁力二维傅里叶变换
软件新增谐波电磁力的3D柱状图显示功能。
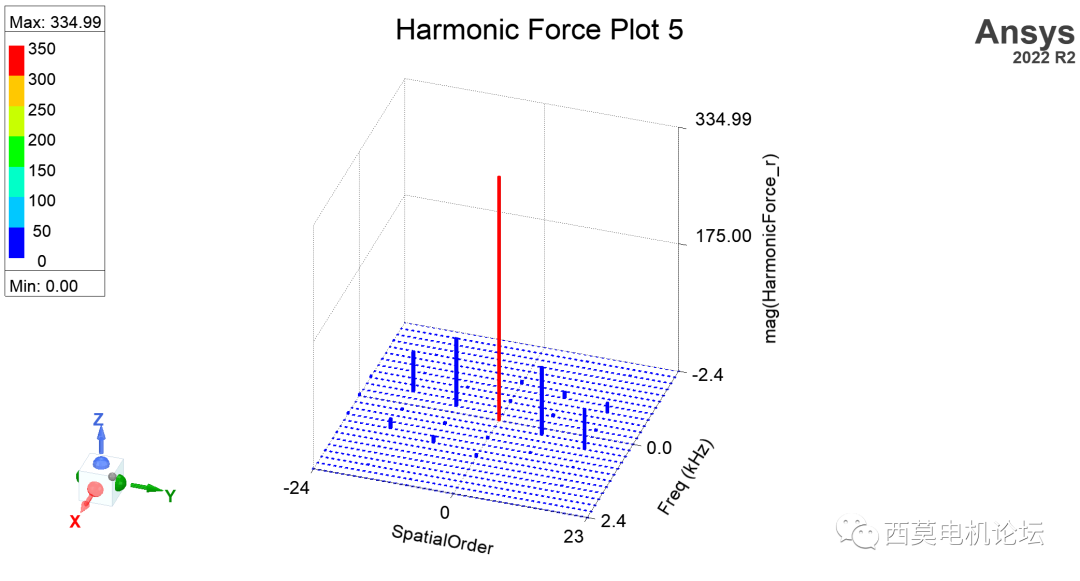
谐波电磁力的3D柱状图显示
关于谐波电磁力的2D结果如下图所示。
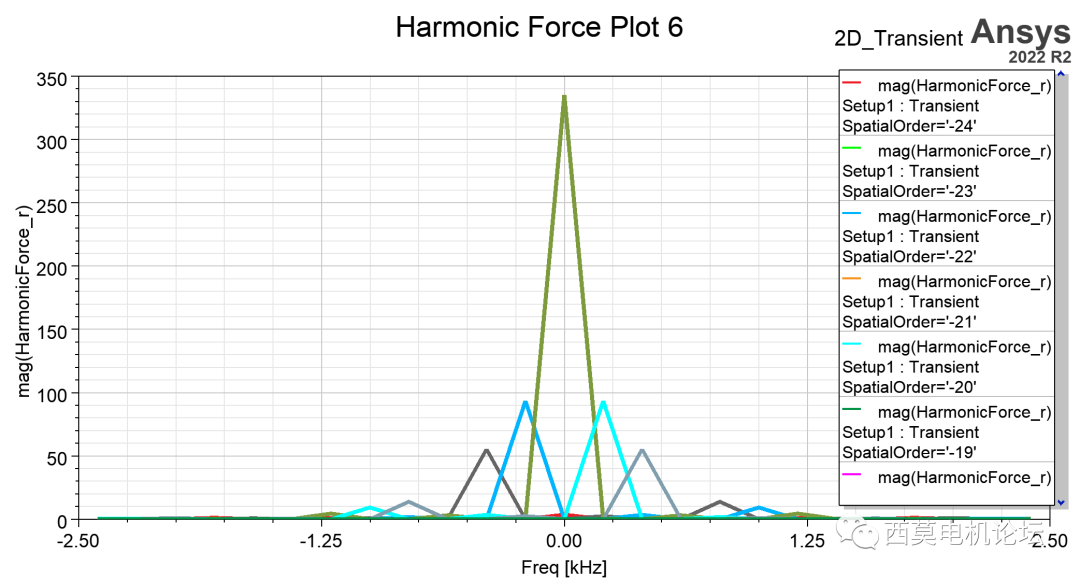
谐波电磁力的2D结果
谐波电磁力结果基于二维离散傅里叶变换,坐标显示为空间阶数和时间频率阶数,支持Mag, Re, Imag, Phase选项,软件基于object based谐波电磁力计算结果进行后处理,因此不需要保存场数据。
新增电磁力二维傅里叶变换功能可以识别引起震动的主要空间和时间阶次电磁力,同时支持电磁力插值(by Inverse DFT)。
2 电机时空二维电磁力谐波的优化设计
接下来将以一V字内置式永磁电机为例,阐述如何利用FFT2D UDO脚本和Ansys optiSLang,对典型的V字内置式永磁电机的电磁力等参数进行敏感性分析与优化。本案例同时展示了如何实现Ansys optiSLang直接调用Maxwell进行优化设计的方法
电机原始设计方案如下。
电机拓扑结构为8极48槽、V字磁钢、转子表面辅助槽。
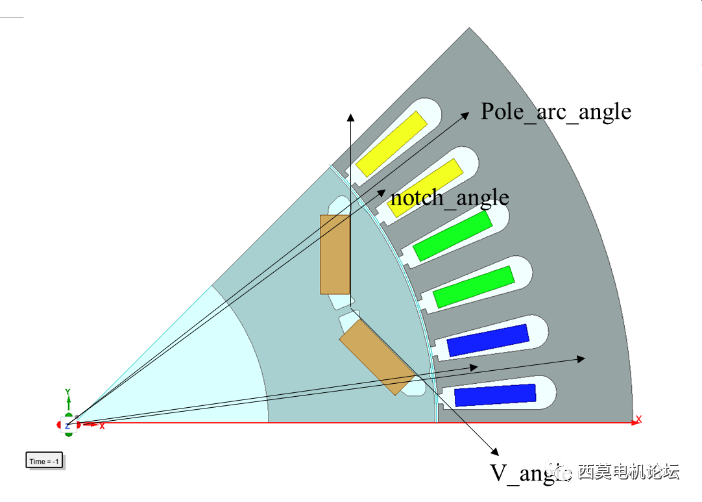
使用 V_Shape_IPM_Rotor UDP 创建转子参数化模型
此处我们选择三个关键转子参数作为设计变量,分别为:
(1) 转子辅助槽圆心角Notch_Angle=120deg;
(2)磁钢V夹角V_Angle=135deg;
(3)极弧角度Pole_Arc_Angle=120deg。
原始方案计算的结果如下。
(1) 平均转矩Torque_avg=189.8Nm
(2) 转矩波动Torque_ripple=21.5%
(3) 磁钢总面积PM_area=97.9mm^2
(4) 电磁力阶次幅值
(a) 时间12阶空间0阶电磁力Force_t12s0=11246.2
(b) 时间6阶空间0阶电磁力Force_t6s0=10462.8
(c) 时间14阶空间8阶电磁力Force_t14s8=7759.8
用户需在Maxwell中创建输出报告,optiSLang会自动提取报告中的数据。
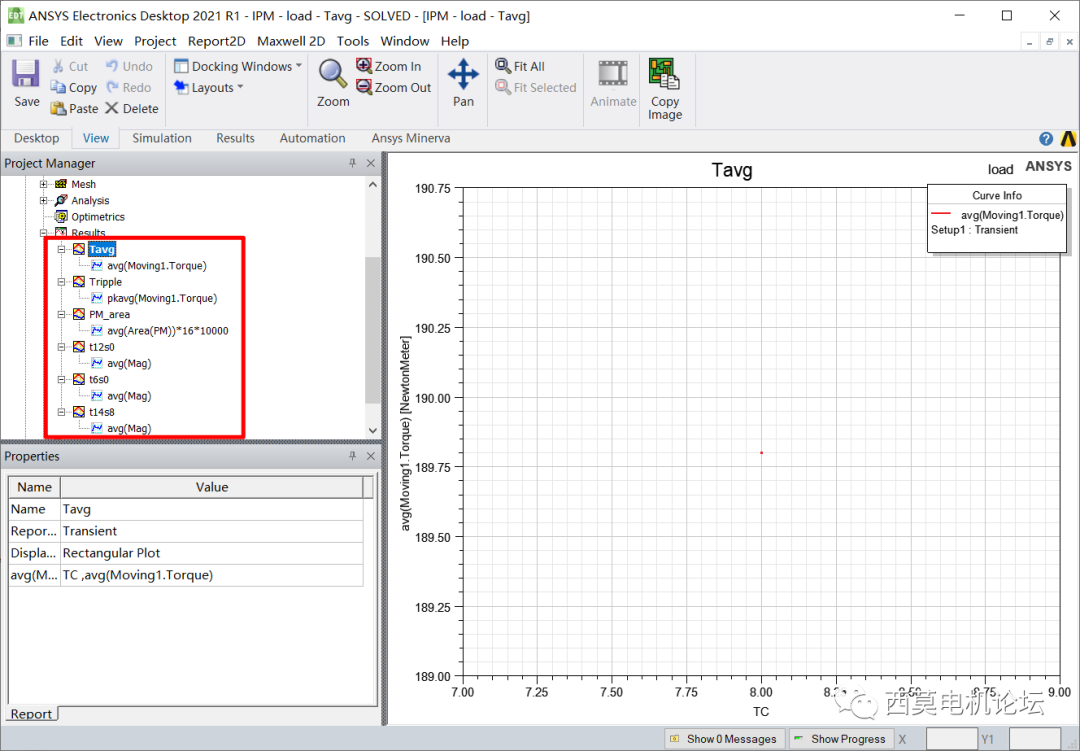
Maxwell中创建输出报告
用户需Maxwell中进行额外设置。默认设置下,每次输出报告刷新后,UDO脚本都会执行一次,当UDO中有大量计算时,这将浪费很多时间。实际上只需最后一个时间步计算结束后执行一次FFT2D,因此我们做如下设置,该设置使Maxwell的报告仅在仿真结束后进行刷新。
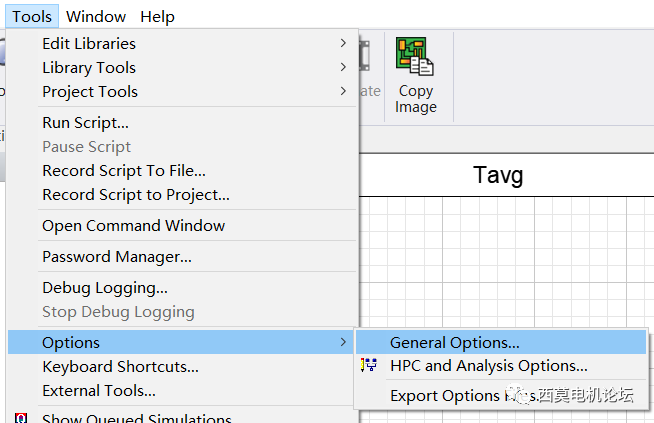
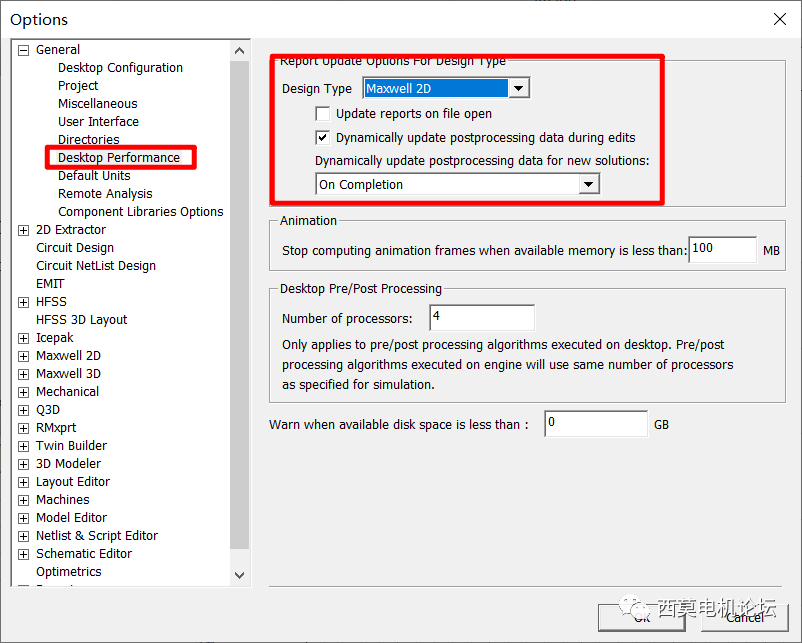
Maxwell中额外设置
接下来进行optiSLang的设置。
首先使用 导入Maxwell模型①。
导入Maxwell模型①。
导入Maxwell模型
然后打开AEDT节点设置②,然后设置ansysaedt.exe路径③,然后使用RegularDSO模式④,然后勾选保存场和网格⑤,选择自动删除AEDT结果文件(可选)⑥,最后保存设置即可⑦。
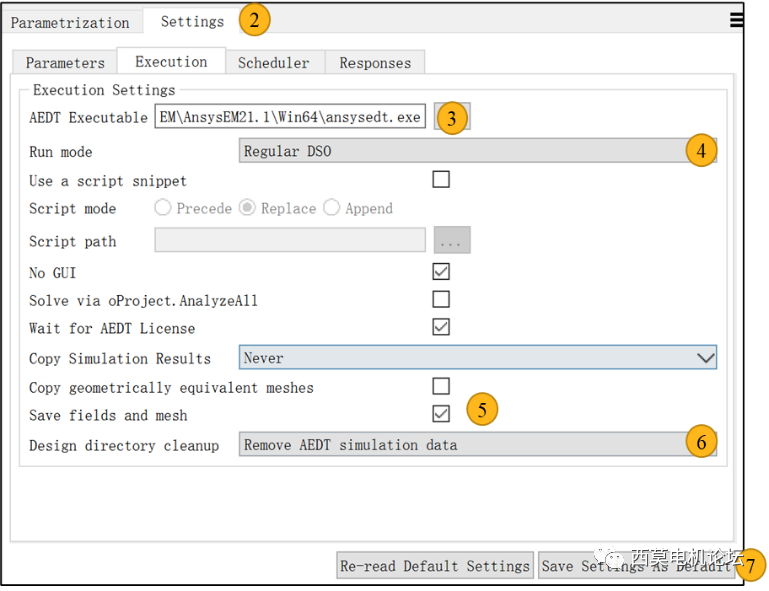
optiSLang设置
接下来设置Parameter参数①,然后设置Response参数②、设置AEDT每次并行求解的设计方案数③、最后设置最大的AEDT求解器并行数④。
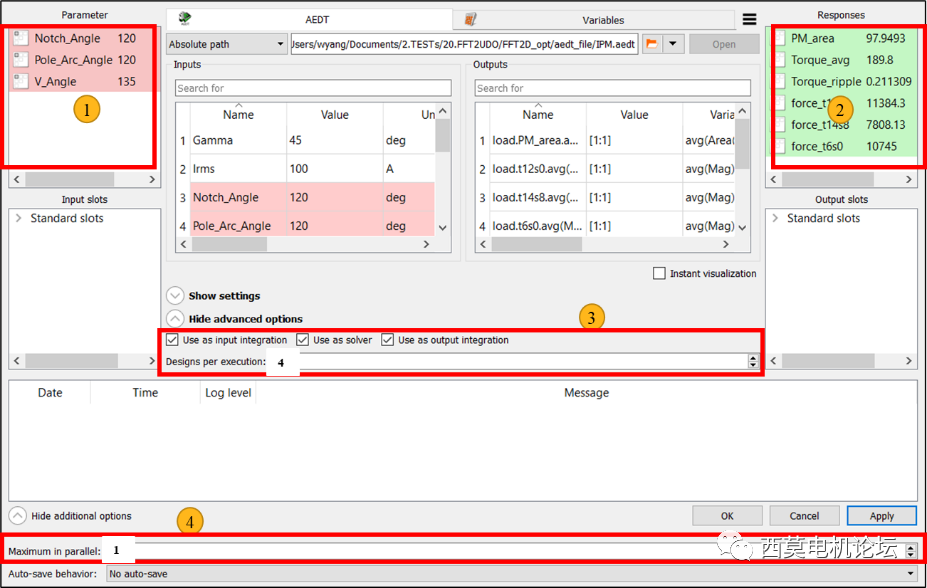
optiSLang设置
接下来进行optiSLang敏感度分析。
optiSLang敏感度分析
然后定义变量范围。
(1) 转子辅助槽圆心角Notch_Angle:90deg~140deg
(2) 磁钢V夹角V_Angle:100deg~170deg
(3) 极弧角度Pole_Arc_Angle:100deg~140deg

定义变量范围
接下来设置采样规则,此处我们使用默认的 Adaptive Metamodel of Optimal Prognosis(AMOP)采样算法。
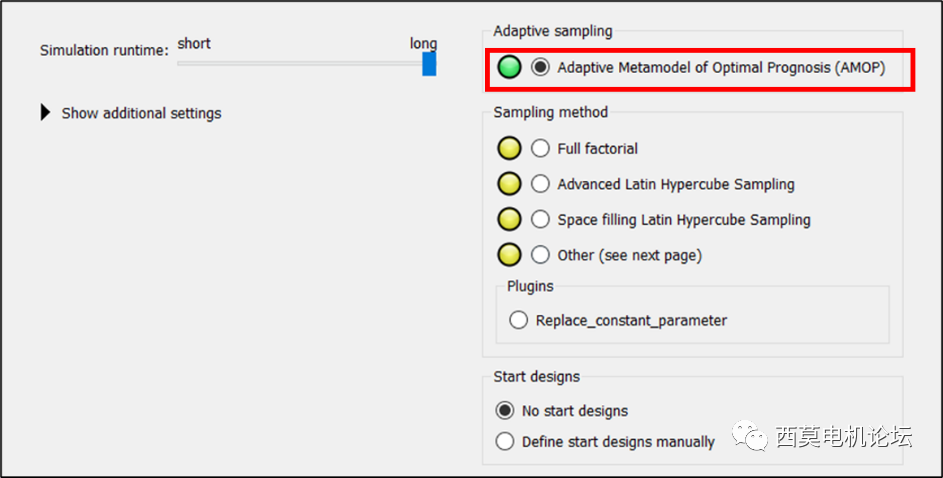
使用默认的 Adaptive Metamodel of OptimalPrognosis(AMOP)采样算法
为了获得高质量MOP模型,需要进行两次AMOP,分别为AMOP Global和AMOP Local两次。AMOP Global为大范围DOE;AMOP Local为局部加密DOE采样,其Local采样基于Glob采样结果。
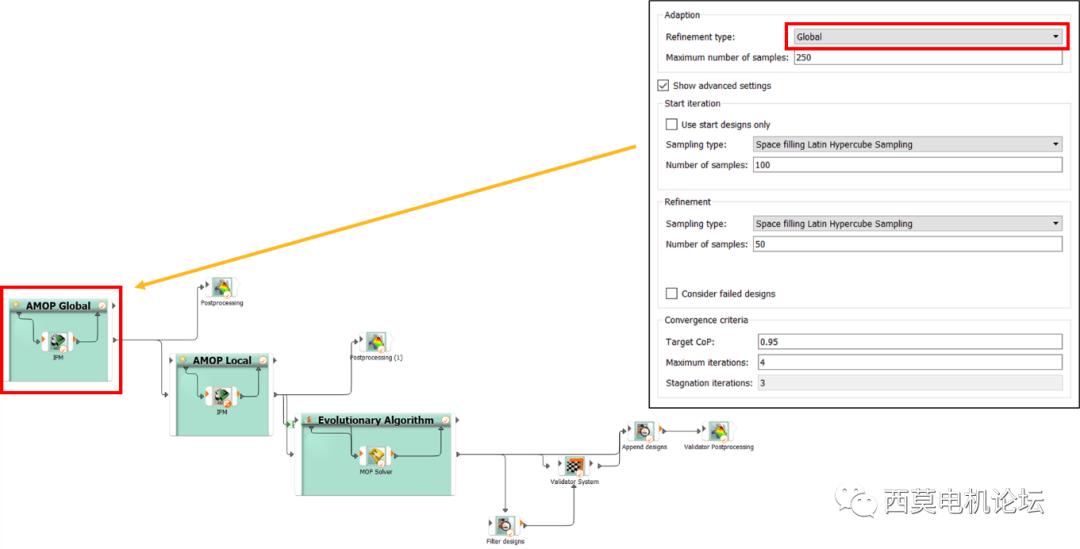
AMOP Global
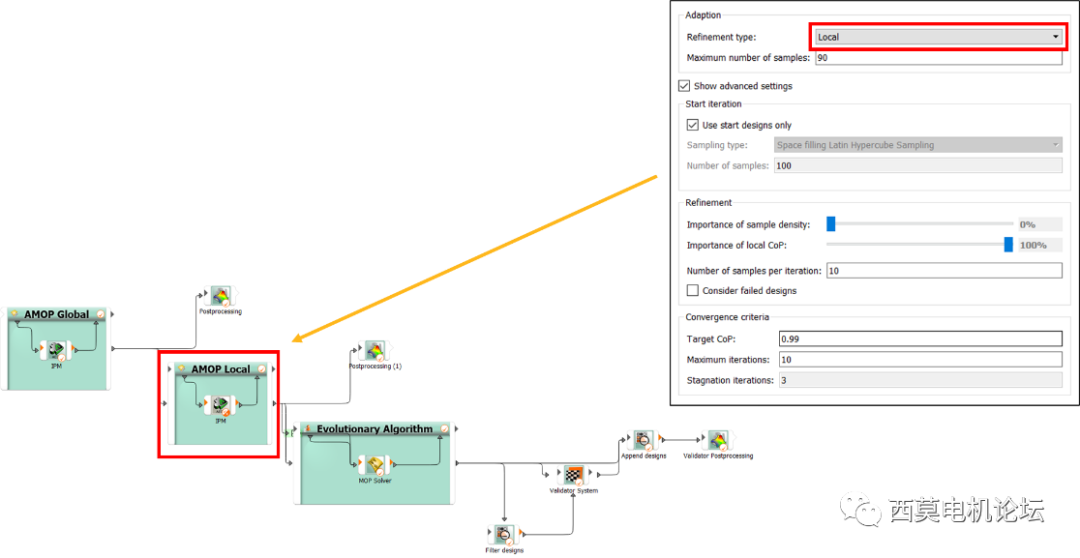
AMOP Local
接下来查看optiSLang敏感度分析结果,经过两次AMOP后,Maxwell共计算340个design,所有响应值都获得了较高精度的MOP模型。AMOP Global及AMOP Local模型分别如下图所示。
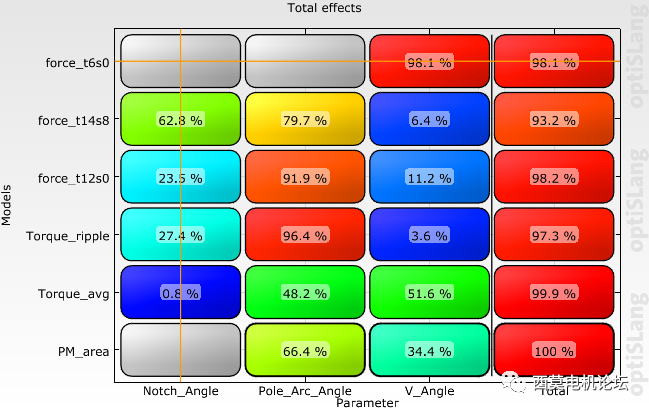
AMOP Global模型
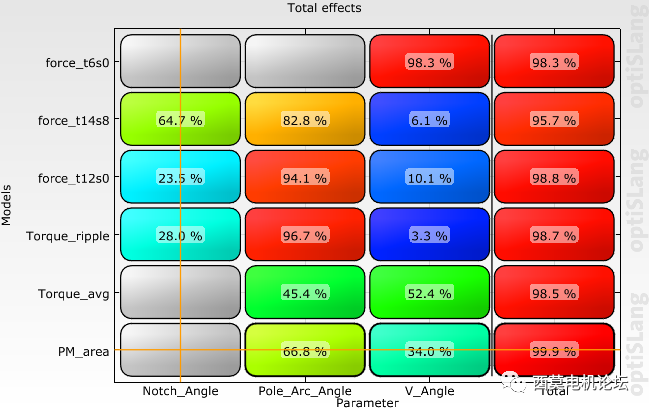
AMOP Local模型
接下来查看参数相关性矩阵,参数相关性矩阵代表输入参数对每个响应值的影响程度,也可以表达不同响应值之间的关系。
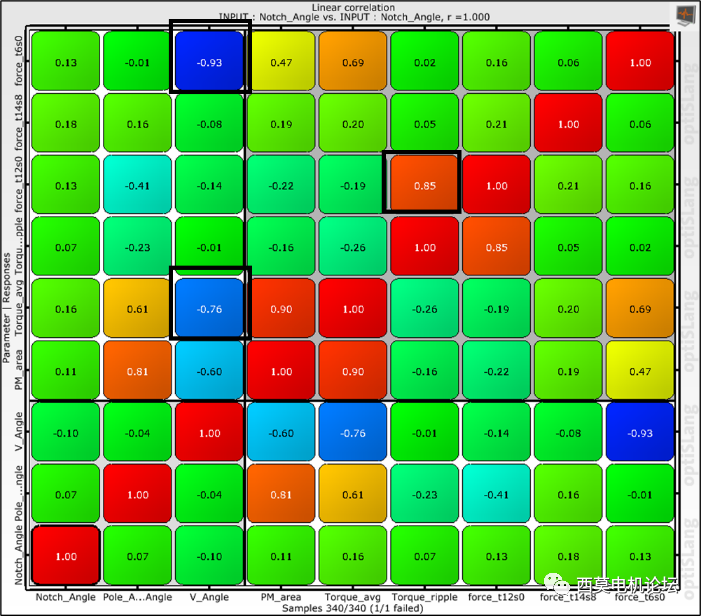
参数相关性矩阵
从参数相关性矩阵结果可看出,V_Angle与force_t6s0、Torque_avg有很强负相关性,且Force_t12s0与Torque_ripple有很强的正相关性。
接下来进行optiSLang优化。优化策略是在平均转矩不变、成本不大幅增加的情况下,尽可能降低振动噪声。因此我们定义优化目标
(1) Torque_avg>=190Nm
(2) Torque_ripple最小化
(3) 各阶次电磁力幅值最小化
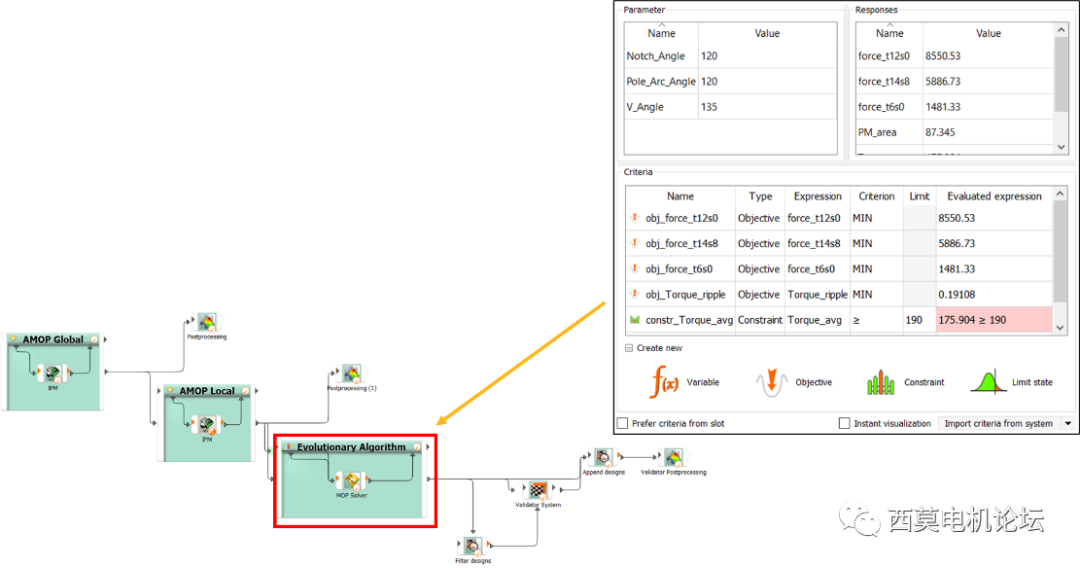
optiSLang优化
接下来选择EvolutionaryAlgorithm优化算法。选择后将会自动添加Validator System。
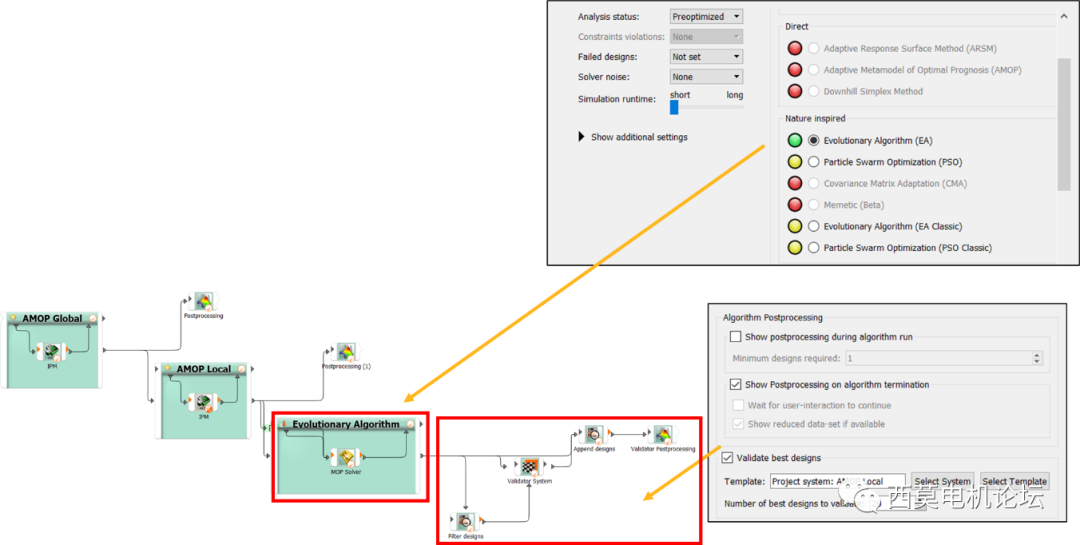
选择Evolutionary Algorithm优化算法
最后,基于MOP模型的优化,10分钟计算了10000个design,其中有8162个design满足约束条件。
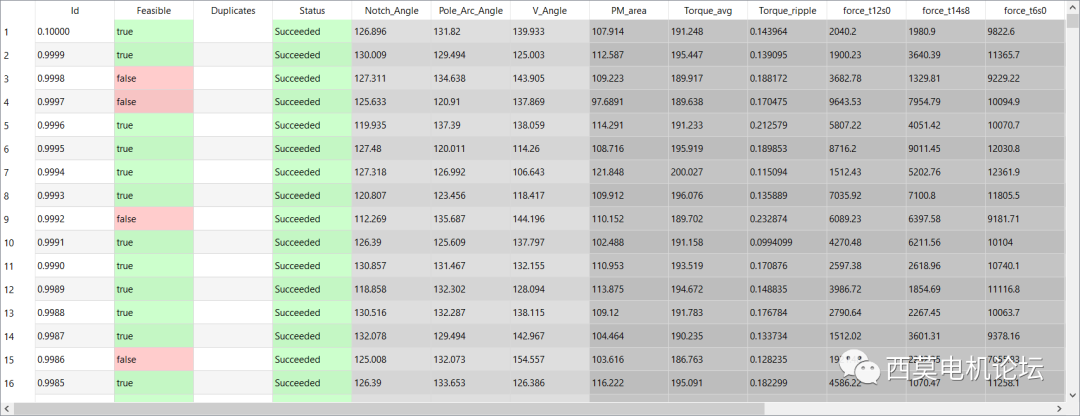
计算结果
通过查看2D帕累托前沿结果,可以发现某些响应值之间出现了较明显的“跷跷板”现象,如下图所示。
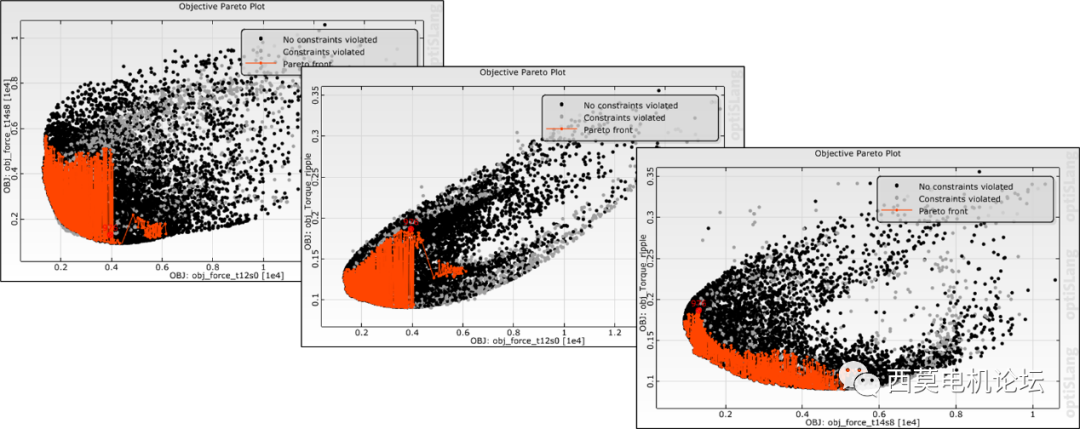
2D帕累托前沿
通过查看3D帕累托前沿结果,可知三个响应(Force_t12s0、Force_t14s8、Torque_ripple)之间形成了明显的帕累托前沿。如下图所示。
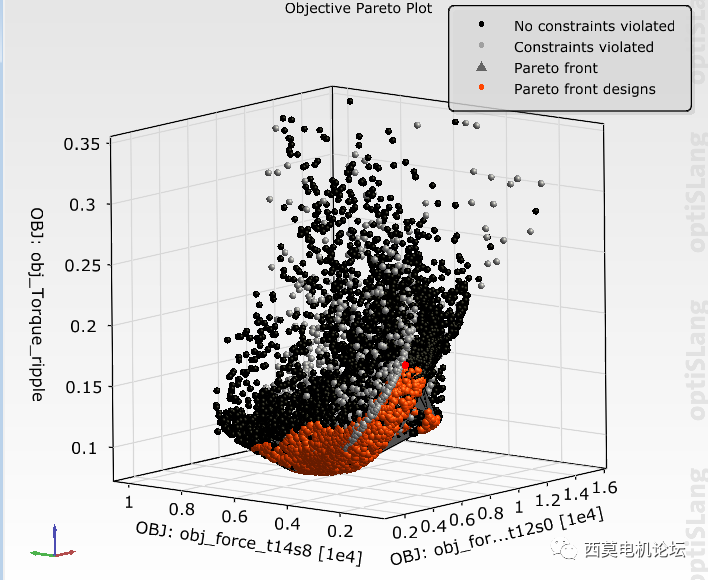
3D帕累托前沿
用户可将MOP计算结果与Maxwell直接计算结果对比。
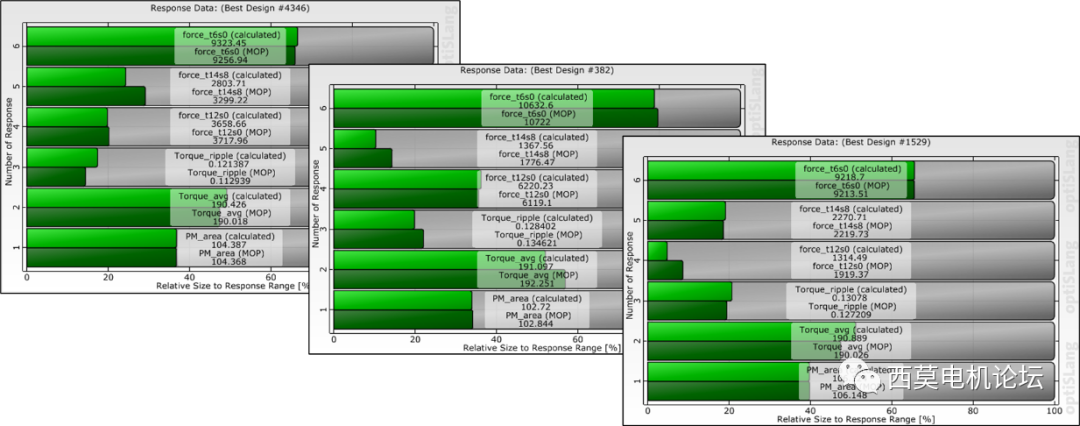
MOP计算结果
用户可使用后处理工具Parallelcoordinates plot分析帕累托前沿解。每一列代表一个输入或者响应值,每条曲线代表一个设计方案。
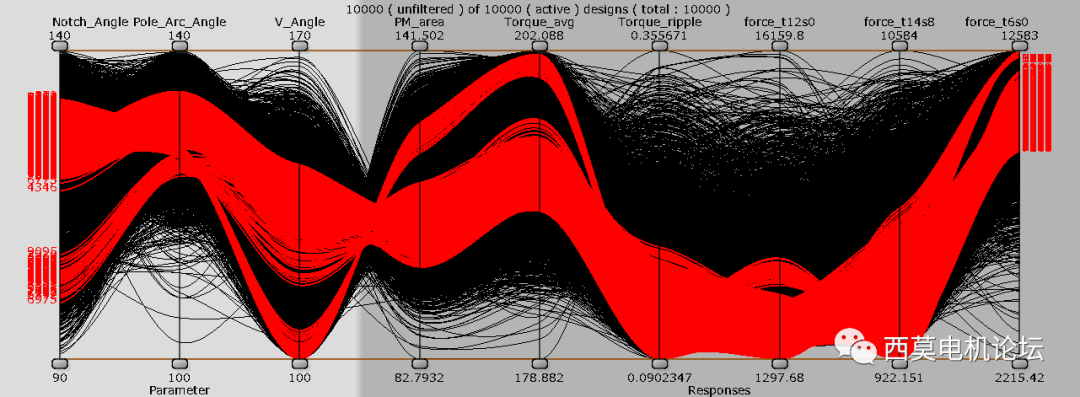
帕累托前沿解
本案例中有1351个帕累托解,用户可使用后处理工具Parallel coordinates plot筛选设计方案,通过拖拽手柄快速缩小解集。
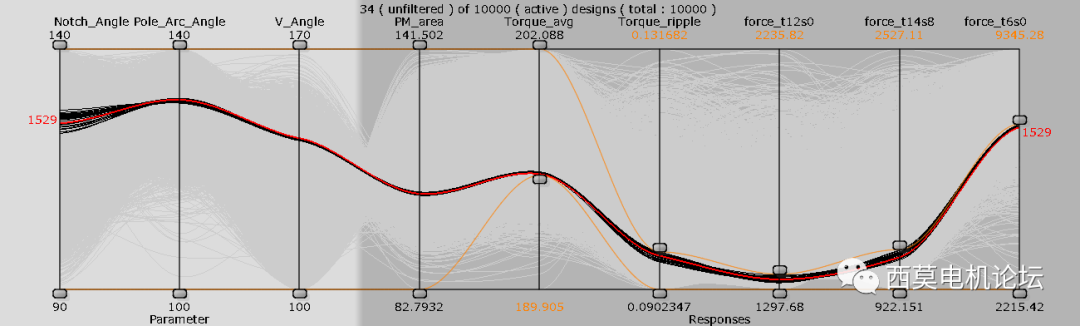
使用后处理工具Parallel coordinates plot筛选设计方案
本案例选择帕累托前沿上的1529号方案作为优化方案。其参数变量取值及目标结果如下图所示。
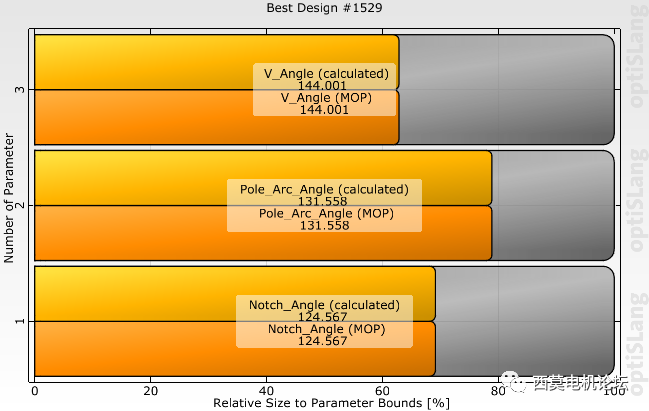
1529号方案变量取值
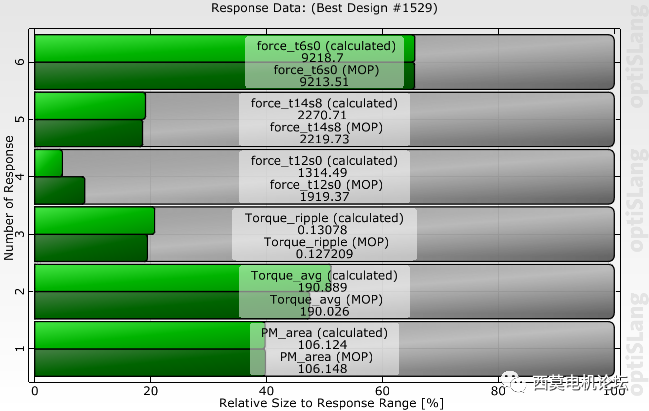
1529号方案目标结果
优化前后对比结果如下表所示。
优化前后对比结果对比表
| 参数 | 优化前 | 优化后 | 对比 |
| Notch_Angle | 120deg | 124.57deg | — |
| V_Angle | 135deg | 144deg | — |
| Pole_Arc_Angle | 120deg | 131.56deg | — |
| Force_t12s0 | 11246.2 | 1314.49 | -88.3% |
| Force_t6s0 | 10462.8 | 9218.7 | -11.9% |
| Force_t14s8 | 7759.8 | 2270.71 | -70.7% |
| Torque_avg | 189.8Nm | 190.9Nm | — |
| Torque_ripple | 21.5% | 13.1% | -39.1% |
| PM_area | 97.9mm^2 | 106.124mm^2 | +8.4% |
优化前后转子结构模型如下图所示。
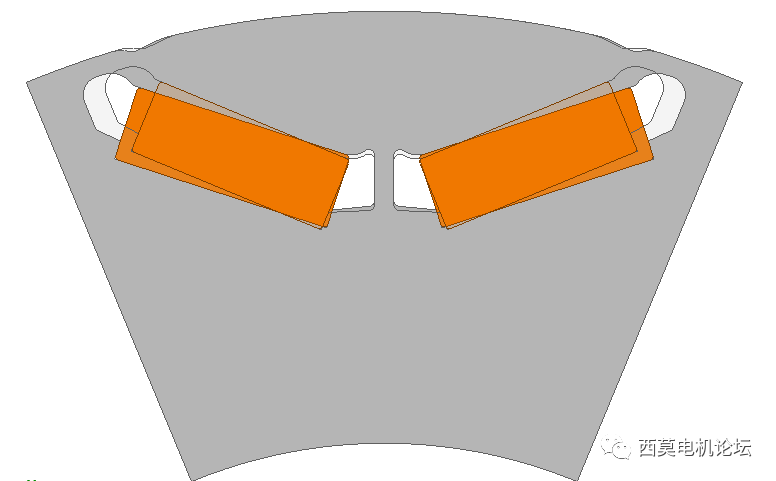
优化前后转子结构模型
优化前后转矩脉动对比如下图所示,红色为优化后方案,绿色为原始方案。
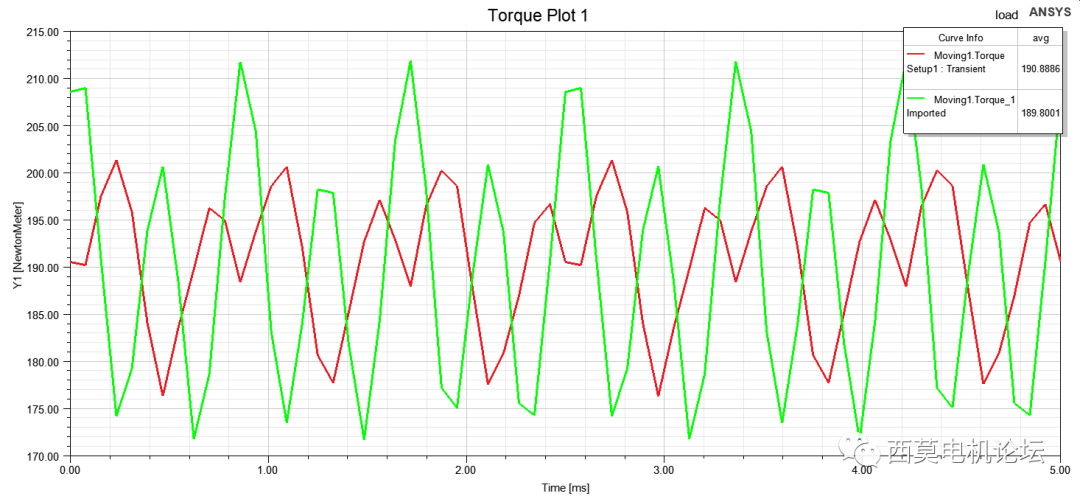
优化前后转矩脉动对比
用户可使用AnsysSound进行阶次分析,分析结果如下图所示。
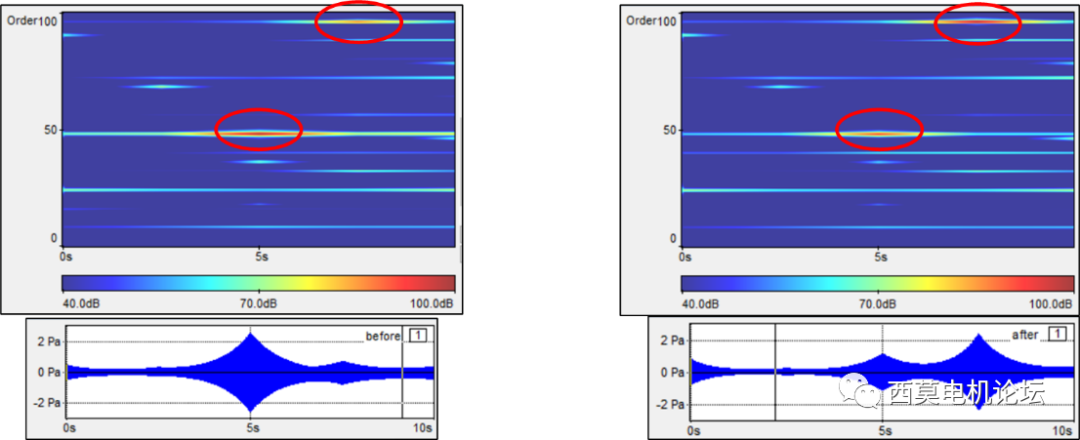
优化前 优化后
从上述结果可知,48阶(force_t12s0)分贝减小,3750rpm@300Hz处由98.89dB下降到91.55dB。而96阶(force_t24s0)分贝增大(未做优化),4875rpm@7800Hz处由86.42dB增加到97.71dB。
用户也可通过AnsysSound生成电机噪音仿真结果,更加直观的对声品质进行评价。
3 总结
Maxwell&optiSLang可高效的实现电机时空阶次电磁力优化。用户可利用UDP绘制非常复杂参数化几何模型,利用UDO进行非常复杂的FEA结果后处理;同时optiSLang强大的优化后处理功能可以帮助用户快速完成方案筛选与验证。
电机阶次电磁力被降阶(MOP)的难度没有想象中那么大,且阶次电磁力会出现“此消彼长”的现象,因此用户在进行NVH优化时,应首先进行定子谐响应分析,锁定所有可能引起较大振幅的空间低阶次电磁力分量,然后将它们全部设置为优化目标或约束条件,以此为目标优化后筛选出的方案将会更加合适。
审核编辑:刘清
-
LabVIEW中怎样将一维数组转换成二维数组2012-04-01 0
-
Ansys Maxwell 3D 2D RMxprt v16.0 Win32-U\2014-06-13 0
-
大神们有了解Ansys Maxwell与Ansoft Maxwell这两个软件的吗?2016-01-07 0
-
电磁仿真软件哪里免费下载2018-01-08 0
-
永磁同步驱动电机径向电磁力致噪声的来龙去脉2021-01-21 0
-
使用VIRTUALLAB FUSION和ANSYS OPTISLANG进行跨平台光学建模和设计2022-09-14 0
-
基于时空二维混沌的数字水印算法2009-07-15 502
-
新手如何入门电磁仿真软件Maxwell的建议2018-02-06 72941
-
STM32二维码与条形码识别库资料合集2021-01-18 1578
-
详解Maxwell电磁仿真过程与结果2021-03-22 25140
-
欧拉 Summit 2021 安全&amp;可靠性&amp;运维专场:主流备份技术探讨2021-11-10 1812
-
电动汽车动力总成噪声分析与优化2023-01-14 4117
-
Ansys Maxwell电磁场仿真软件提升机电系统性能2023-02-14 3050
-
Ansys二维光栅出瞳扩展系统优化2023-05-23 714
-
基于Ansys Workbench的Maxwell&;amp;optiSLang永磁电机联设计2023-08-24 10255
全部0条评论

快来发表一下你的评论吧 !

