Hilbert(希尔伯特)变换的两种Matlab实现方法

实信号只包含振幅信息，而缺乏相位信息。而复信号则包含了原始信号的相位信息，可以用于分析信号的相位特性。在某些应用中，例如信号处理、通信系统中，相位信息对于理解信号的特性和进行后续处理非常重要。

Hilbert（希尔伯特）变换可以将实信号转换为复信号，常用于提取信号的相位信息，使得我们能够更全面地分析和处理信号，这在雷达通信领域中都很有用，尤其是在带通信号处理中。

Hilbert变换可以认为是函数f(t)和h(t)的卷积，其中：

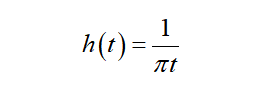
在频率域，对函数进行Hilbert变换，是在f(t)的傅里叶变换结果F(w)前乘一个系数H(w)，其中H(w)是h(t)的傅里叶变换：

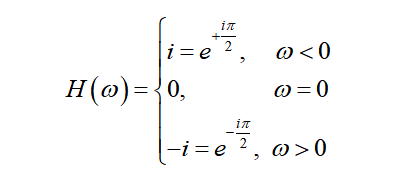
也就是把F(w)所有正频率向后移动90°相位，负频率则向前移动90°相位。也可以用符号函数表示：

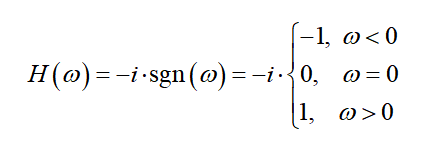
那么，对于函数f(t)，它的希尔伯特变换在频域表示为：

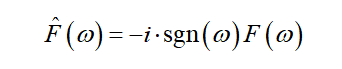
方法一：使用Matlab工具箱中的函数使用Matlab工具箱中的函数 hilbert 可以计算实数输入序列 x 的 Hilbert 变换，并返回相同长度的复数结果，即 y = hilbert(x)，其中 y 的实部是原始实数数据，虚部是实际 Hilbert 变换。

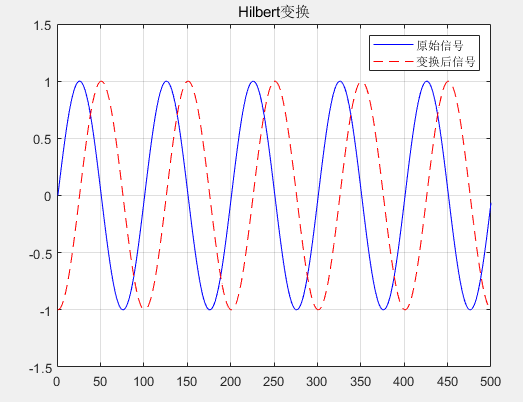
方法二：使用FFT/IFFTHilbert变换的实现还可以通过对实信号进行傅里叶变换（FFT），将负频率部分置零，然后再通过逆傅里叶变换（IFFT）转换到时域，得到复信号，其中实数部分为原始信号，虚数部分为变换后的信号。

常见函数的Hilbert变换

另外，使用NCO（Numerically Controlled Oscillator）和低通滤波器的组合也可以直接将实信号转换为复信号，避免了额外的FFT和IFFT处理，从而减少处理时间。

审核编辑：汤梓红