1.逆变器非线性

这里将逆变器非线性分为两个部分来介绍。第一部分是管压降带来的非线性，第二部分是死区时间带来非线性。

1.1 管压降非线性

在逆变器中，各种器件并不是理想的特性。管压降造成的非线性即开关器件的导通压降和反向并联二极管的导通压降造成的输出电压与指令电压不一致的情况。以A相桥臂为例进行分析。图1是三相逆变器中A相桥臂输出电流到电机绕组时的情况，定义此时电流为正方向。

在A相电流为正时，桥臂的导通有两种情况，即A相桥臂上管导通（ Sa =1）和上管关断（ Sa =0），分别如图1（a）和图1（b）所示。在图1（a）中，上管导通（ Sa =1），此时电流从电源正极端经过开关管流向绕组，经过开关管S1时压降为 Vce 。

因此电流为正上管导通时a点电压为Va0 = Vdc /2- Vce 。类似的，在图1（b）中，上管关闭（ Sa =0），此时电流从电源负极端经过反并联二极管向绕组续流，经过S1旁二极管时压降为- Vd 。因此上管关闭时a点电压为Va0 =- Vdc /2- Vd 。

图1 A相电流为正时的非线性分析

图2 A相电流为负时的非线性分析

图2是电流为负时的情况。与电流为正时的理论一致，可以得出当 Sa =1时，Va0 = Vdc /2+ Vd ；当 Sa =0时，Va0 =- Vdc /2+ Vce 。

总结以上四种情况，可以得到表1所示的A相端电压的公式。

表1 逆变器非线性端电压计算

由于功率器件的管压降中除了导通特性，还有一部分是电阻性压降，因此，开关器件和二极管的压降通常可以表示为

（式1）

其中，Vce0和Vd0是功率器件的阈值电压，rce和rd是功率器件的等效电阻。

从而，A相端电压可以表示为 （式2）

需要注意的是，在表1的公式中，只考虑了管压降造成的非线性。在下一节，将对死区时间造成的非线性进行讨论。

1.2 死区时间非线性

图3表示了在PWM调制过程中，参考导通时间和实际导通时间的关系。图3（a）中是通过参考电压计算出的参考导通时间。由于开关管并不是理想的开关器件，导通和关断动作都有延迟。为了防止同一个桥臂的上下管同时导通，需要设置死区时间来避免同一桥臂上下管同时处于导通或者关闭过程，如图3（b）所示，为了避免下管未完全关闭时上管导通或者上管未完全关闭时下管导通，所以设置死区时间Tdead来避免两个开关管同时导通。

假设A相桥臂上管导通时间应该是 Ta_ref ，那经过死区时间调节后，导通时间变为了 Ta_ref - Tdead 。另外，将图3（b）的PWM信号施加到开关管上时，正如前面所提到的，由于开关管的导通和关闭过程并不是理想的，导通和关断的延迟时间分别为Ton和 Toff 。

图3 考虑死区时间的开关时序

最终，结合图3（c）以及图1（a）所示，当电流为正时，A相上管的实际导通时间为

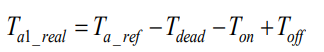（式3）

同理，结合图3（c）以及图2（b）所示，当电流为负时，A相下管的实际导通时间为

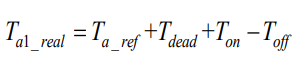（式4）

综上可得

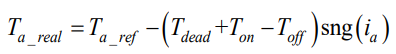（式5）

（式6）

另外，B相和C相的端电压计算公式为

（式7）

（式8）

1.3 相电压计算

前面分析了考虑管压降和死区时间的非线性三相端电压的计算。如图所示，端电压推导的是abc点到0点的电压。但是在实际分析中，我们需要的是相电压，即abc点分别到N点的电压。因此，上一节的分析结果还需要进一步推导。

图4 三相逆变器示意图

根据图4可知

（式9）

而

（式10）

联立（式9）和（式10）可得三相电压的计算公式为

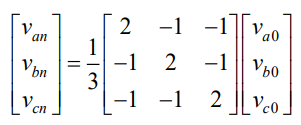（式11）

更进一步的，联立（式6）、（式7）和（式11）可得非线性相电压的表达式是

（式12）

从（式11）也可以得到不考虑非线性的相电压的表达式（理想相电压）为

（式13）

以A相为例，联立（式12）和式（13），可以得到功率器件管压降和死区效应对相电压造成的非线性误差为

（式14）

其中 （式15）

同理，B和C相也可以推导出来，总结三相非线性电压误差的表达式为

（式16）

对（式16）进行Park变换，可以得到dq轴电压的误差公式。

（式17）

在开始下一节之前，需要解释的是，这里没有考虑直流母线电压的测量误差。如果考虑这一点，公式会变得更多更复杂，但是增加这部分分析对本文的主旨帮助不大。因此，为了简化分析，假设母线电压是准确的。

2.非线性补偿

通过分析和推导，在上一章得到了非线性相电压及其误差、dq轴误差电压的表达式（式17）。根据式17，可得到如图5为dq轴误差电压的示意图。在一个电周期中，dq轴误差电压波动了6个周期。也就是说dq轴误差电压的频率是基频的6倍。旋转坐标系中6倍频的波动会在三相静止坐标系中造成5/7次波动。或者说是三相电压中的5/7次谐波表现在旋转坐标系中是6倍频的波动。如果有对这个结论不明白的读者，可以在下一章多级旋转坐标系理论中得到答案。

图5 dq轴误差电压

如图6（a）所示为非线性相电压的波形，从相电压波形中也可以明显看到逆变器非线性对相电压波形造成的影响。同时，对图6（a）中的相电压进行谐波分析，如图6（b）所示。可见，5/7次谐波在相电压中占主要因素，因此，逆变器非线性在相电流中带来的谐波也是5/7次。

图6 考虑逆变器非线性的相电压波形（a）相电压（b）谐波分析

图7 dq轴非线性电压对比

如图7为使用仿真得到的考虑非线性因素之后的相电流波形与之对应的谐波分析。可见两者比较接近。

图8 相电流及其谐波分析

如图8为考虑逆变器非线性因素后的相电流波形及其谐波分析，可以看到，5/7次谐波是主要谐波分量。THD为14.33%。

针对逆变器非线性造成的低频谐波，最直接的方法是利用前面推导得到的误差电压对指令电压进行补偿。图9为非线性电压补偿的框图。根据计算的非线性dq轴电压，在电流环输出的参考电压后进行补偿。

图9 非线性电压补偿

图10为对电压进行补偿前后，相电流及其谐波分析。在红色点线时刻进行非线性电压补偿，补偿之前，相电流的THD为14.33%，补偿之后THD降为6.63%。可见非线性电压补偿具有明显的电流谐波抑制效果。

图10 非线性电压补偿前后电流波形及其谐波分析

当谐波含量较少时，逆变器非线性补偿可以将谐波抑制。但是在谐波含量较高的情况下，由于相电流在过零点处有抖动，造成计算出的非线性电压误差抖动增大。这部分抖动会在环路中对电流谐波造成一定影响，达不到补偿非线性电压的目的。

3.指定谐波次数抑制

指定谐波次数抑制法是一种简单有效的谐波抑制方法。三相电流的k次谐波表达式为：

（18）

式中， iak 、 ibk 、ick分别表示三相对称PMSM的ABC相的k次谐波电流；Im表示k次谐波电流的幅值；φk表示相对应的谐波电流的初始位置。

很明显， iak 、 ibk 、ick三者之间的相序会随着k取值的不同而不同：当k取值为 k =3 n +1（ n =1,2…）时，iak超前ibk2π/3且滞后ick2π/3，相序和基波一样，称为正序谐波电流；当k取值为 k =3 n -1（ n =1,2…）时，iak滞后ibk 2π/3且超前ick2π/3，相序和基波一样，称为负序谐波电流；当k取值为 k =3 n （ n =1,2…）时，iak 、 ibk 、ick幅值相等，相位一致，称之为零序电流。以5/7次谐波为例进行分析。由前面分析可知：相电流中的5次谐波是负序的，7次谐波是正序的。此时，ABC三相电流可以表示为：

（19）

式中，Im1表示基波幅值；Im5 、θ5表示5次谐波的幅值和初始时刻的相位；Im7 、θ7分别代表7次谐波的幅值和初始时刻的相位。

以5次谐波分量为例。从ABC坐标轴系下变换到5次d-q坐标轴系下的变换矩阵为：

（20）

从5次到基波的dq变换矩阵为：

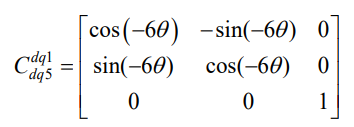（21）

从基波到5次的dq矩阵为：

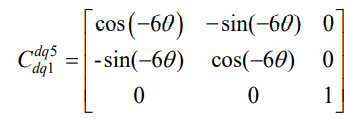（22）

因此，在5次旋转坐标系下，5次谐波电流的d-q分量以直流分量的形式呈现，基波和7次谐波以交流分量的形式呈现。

（23）

然后，对需要抑制的谐波分别建立电流环，并设置给定值为0。最后，将各个次数电流环产生的电压信号在静止坐标系中与基波相叠加，即可以达到对电压进行补偿，达到谐波抑制的效果。指定次数谐波抑制控制系统的框图如图11所示。谐波抑制模块框图如图12所示，图12以5次谐波为例。ABC三相电流首先经过5次dq变换，然后通过低通滤波器得到5次旋转坐标系下的dq电流，再与给定值进行比较，从而调节该次谐波为0。变换后的电压与基波电压在静止坐标系中叠加，作为补偿电压。

图11 控制系统框图

图12 谐波抑制补偿电压计算

指定谐波抑制法介入控制系统前后电流波形如图13所示。同样的，在红色点线时刻开始进行谐波抑制。谐波抑制之前，相电流的THD为14.33%，补偿之后THD降为4.18%。可见非线性电压补偿具有明显的电流谐波抑制效果。但是，由于低通滤波器的延迟效应，该方法需要几个电周期来进行调整。

图13 相电流及其谐波分析

4.比例-积分-谐振控制器

传统的电流控制器使用PI控制器。由于直流信号中低频分量占主要部分，因此PI控制器对于直流信号有较好的控制效果。通过前面的分析可知，逆变器非线性对于dq轴电压造成的波动频率为基频的6倍。通常电机电流环的带宽只有几百Hz级别，6倍频的情况下，dq轴电压波动频率会达到kHz以上。PI控制器对逆变器非线性带来的波动是无能为力的。

在这种情况下，可以使用比例积分谐振（PIR）控制器。PIR控制器即在PI的基础上并联了一个谐振单元。谐振单元可以在dq轴电压波动频率处提供较大的增益，从而提高电流控制器对于交流信号的控制能力。PIR控制器的传递函数如下。

（24）

式中，Kp是比例系数，Ki是积分系数，Kr是谐振系数，ωc是谐振带宽，ω0是谐振频率。

考虑永磁同步电机的等效传递函数为

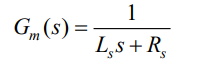（25）

式中，Ls是定子电感，Rs是定子电阻。

则可以得到使用PI控制器和PIR控制器时的电流环开环传递函数分别为式（26）和式（27），考虑逆变器和采样计算等造成的延迟时间为 Td 。

（26）

（27）

使用PI和PIR控制器时电流环开环传函的频率响应如图14所示。其中红色曲线为PIR控制下的bode图，黑色为PI控制下的bode图。从bode图中可以看出PI的增益穿越频率为100Hz，而PIR在100Hz处也穿越了0dB。但是，由于谐振单元的作用，PIR电流环的增益在180Hz（谐振频率）增益显著升高且保持了45度左右的相位裕度。与之对应的，PI电流环的增益在180Hz时已经为-6dB。图15为PIR谐波抑制方法的控制框图。

图14 两种控制器频率响应对比

图15 PIR谐波抑制框图

比例积分谐振谐波抑制法介入控制系统前后电流波形如图16所示。在红色点线时刻开始进行谐波抑制。谐波抑制之前，相电流的THD为14.33%，补偿之后THD降为4.53%。可见非线性电压补偿具有显著的电流谐波抑制效果。但是，该方法参数设置较困难，容易在动态时出现系统不稳定的情况。

图16 PIR谐波抑制框图