量子计算场景实用秘籍：开物SDK之subQUBO算法分解

在各行业应用场景的数学模型构建中，经常会遇到实际问题的计算规模巨大，模型所包含的变量数超出现有量子计算机比特数的情况，导致无法直接使用量子计算机进行求解，而是先要对原问题进行拆分，这时就需要一种称为“subQUBO算法”的帮助。

  subQUBO算法是一种将大规模组合优化问题分解为若干个小规模问题以便能在当前中小规模量子计算机上实现求解的方法。它的核心思想是通过软件手段将原问题拆解，并融合经典和量子两种模型，重构成一种“量子计算+经典计算”混合架构的全新数学模型，从而使得现有的光量子计算机能够直接处理，同时，该算法可以确保被分解后的小问题集合在求解质量上，仍旧与原有大问题是完全一致的。这项非常实用的模型预处理功能，也是玻色量子发布的开物SDK强大能力之一。

  subQUBO算法的应用场景主要集中在解决大规模优化问题中，尤其是在受到当前量子计算机比特数限制而难以直接求解的问题上。例如，生物制药领域的药物发现和网络科学领域的社区发现两大典型场景案例。

    药物发现场景      

药物发现作为生物制药领域的核心环节，致力于寻找对特定疾病具有疗效的潜在药物分子，包括了靶标鉴定、药物设计，合成、评价等多个步骤。其中，分子对接作为药物发现早期虚拟筛选、药物设计的重要技术手段之一，多被用于预测和分析配体（小分子化合物）与受体（蛋白质或核酸）之间的结合过程。

通过计算配体受体之间的空间互补以及能量匹配来寻找其最佳的复合物模式。我们将分子对接过程中的构象采样问题转化为配体原子和受体结合口袋的空间格点匹配问题，通过构建QUBO模型可以在相干光量子计算机上实现求解，再将求得的解转换为空间位置以最终获得复合物pose信息，从而加速了分子对接的计算过程，并且还能有效的提高分子对接的规模和质量。

但是，当配体和受体的分子量较大时，或是可选的受体结合口袋较多时，原有的QUBO模型所包含的变量数也会随之增加，这就对量子计算机的比特规模提出了更高的要求。这时我们通过subQUBO方法就可以从原QUBO问题中抽取出部分变量形成若干子问题，并通过迭代更新来优化求解过程，使得分解后的问题求解结果能够不断逼近最优解。

    社区发现场景      

网络科学是利用数学理论研究数据网络的学科，重点在于分析和表征网络行为。现实世界网络的一个重要特征是它们具有社区结构，这可以通过图方法来实现建模。识别社区结构是理解不同网络结构的重要手段，在社交网络、金融风控、生命科学等领域都有巨大应用价值。

尤其在大规模网络中，检测社区结构更加有价值，有许多应用产品都是使用社区检测算法来揭示网络中的隐藏信息。例如，在社交网络中找到具有相似行为的用户，通过他们的购物习惯对电子商务中的客户进行分类能够有效提升营销成功率。同样，社区检测在设计延迟容忍网络中的网络协议和在线社交网络中的蠕虫遏制中能够发挥重要作用。在数据网络中，识别恶意用户社区是很有帮助的。在智能营销中社区发现具有一些有趣的应用，例如增强在线购物者、产品推荐和定向广告。在大型购物网络中，社区检测可以用于分类客户并根据他们的购买历史提供未来购买的建议。

社区检测算法的性能在很大程度上取决于网络的拓扑结构，网络可以是静态的或动态的。模块度最大化和谱聚类分别被认为是静态网络中社区识别的主要方法。我们将传统的基于模块度的社区发现模型转化为QUBO形式，并使用玻色量子的相干光量子计算机实现了求解。而往往在实际场景中，在线网络用户数或者生命科学领域的细胞数量非常庞大，所涉及的计算规模都会超过现有量子比特数量的限制，那么我们就可以借助subQUBO算法算法，进行问题拆分，最终完成求解。

    QUBO问题的分解       一个较大的QUBO优化问题，在固定一部分变量的取值后，可以形成一个更小的QUBO优化问题。

令原始的QUBO问题为：

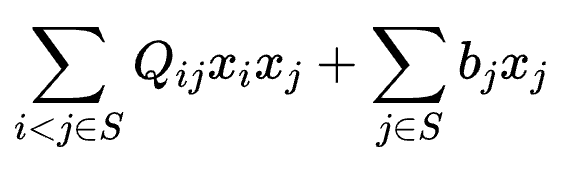
令可活动变量下标集合为Sf。令固定的变量下标集合为Sc=SSf，取值为

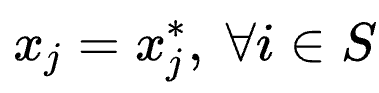
如此，原始的QUBO问题可改写为以xi∈Sf为变量的问题：

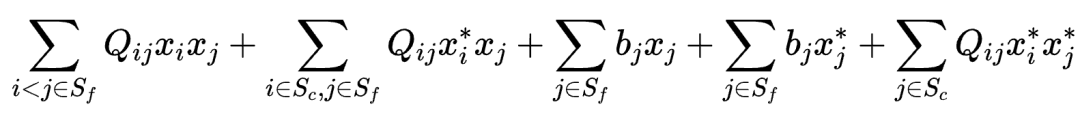
其中，二次项为：

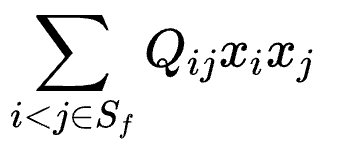
一次项为：

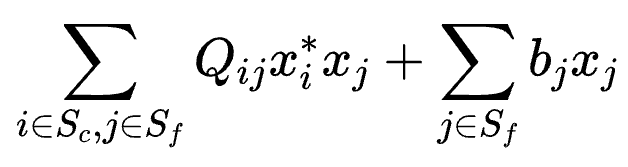
常数项为：

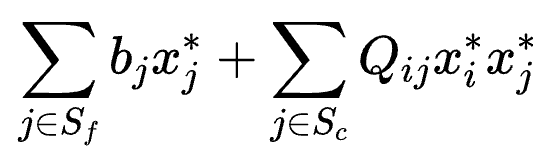
忽略常数项，则有：

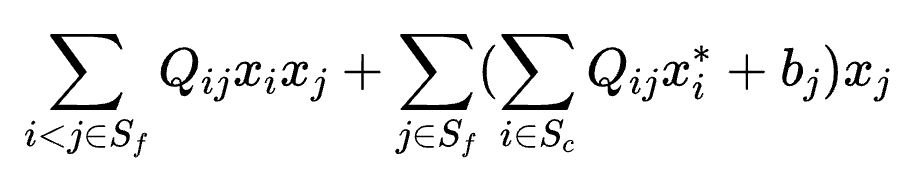
相干光量子计算机直接求解的Ising模型和QUBO模型是等价的，在实现时直接对Ising模型抽取子问题也可以达到同样的作用。优化过程：

如伪代码所示，通过subqubo优化时，首先要确定初始解向量，之后的求解过程不断更新解向量。之后的迭代过程中，需要执行的操作包括子问题变量集合的选取，子问题的求解与更新答案，全局优化。

子问题变量集合的选取：

变量集合的选取有很多不同的策略，策略的选取取决于实际问题。选取的策略包括：

（1）将QUBO问题看成一张图，根据图的连通性选择子问题

（2）有限选择重要的或者当前不确定程度更高的变量

（3）根据实际问题的结构选择，如选择在实际问题中相关的变量

子问题的求解与更新答案：

参考前一节问题的分解，我们在选取变量集合之后就可以用原问题和当前的解生成新的子问题。子问题的变量就是我们所选的变量集合。求解子问题之后，将变量的改变在原问题的解中做相应的更新。有时subQUBO算法会维护一个解集合，这只需将新产生的解加入到解集合中并对维护的解集作相应更新。

    全局优化      

每次优化都只考虑使用同一标准选取的一部分变量，有时候可能会导致算法错过一些变量。通过禁忌搜索，模拟退火等算法，引入不同的优化方式，可以帮助跳出局部最优。

    子问题如何选取？      

本节以选择不确定程度更高的变量为例，讲解子问题的选取过程。

当被固定的变量都已经得到最优解，那么subQUBO表达式的最优解与QUBO表达式的最优解相同。因此，合理的方式应该是将有更高概率已经获得正确解的变量固定，subQUBO表达式选取难以确定最优解的变量。

于是，该方法通过之前求解时获得的解来判断每个变量当前的解有多大信心为正确解，结果多数为1则为1，多数为0则为0，1和0的次数差不多说明难以确定。具体操作为通过 |解为1的次数-求解次数/2| 来判断。

当该值较大时，变量有较高信心为1或0的某一个值，反之则说明难以判断该变量的值应该为1或0，应该优先加入subQUBO。

    总结      

现实中的问题普遍存在大规模求解的情况，subQUBO算法为用户提供了一种全新的解决思路，并证明其是一种用于解决大规模QUBO问题的有效方法。它通过将原始问题分解为多个子问题，并在迭代过程中优化这些子问题的求解效果，从而逐步逼近全局最优解。

在药物发现和社区发现等实际应用中，subQUBO算法能够处理超出量子计算机比特数限制的问题，提高了量子计算能够覆盖到的问题规模。并且子问题的选取策略也是多样的，可根据实际问题特点选择合适的变量集合。

显然，通过结合经典算法和量子计算，subQUBO算法为解决复杂优化问题提供了新的思路和方法。基于玻色量子自研的开物SDK，用户只需关注建立与场景所对应的数学模型，SDK提供的方法可以自动完成问题分解，用户无需担心其背后的复杂度，这将极大的降低用户使用相干光量子计算机求解实际问题的难度。

文章来源 ：玻色量子  在此特别鸣谢！