

量子计算场景实用秘籍:开物SDK之“高阶函数降阶”
描述
现实应用场景往往具有复杂的多变量交互作用和非线性行为,在数学上均属于高阶问题,存在于实际应用中的各个领域,如图像处理中的去噪和超分辨率、工程设计与优化、金融工程中的期权定价和投资组合优化、医疗领域中的治疗方案优化和药物代谢过程等。
在现实应用中,解决高阶问题充满挑战。一是容易陷入局部最优解。高阶问题通常涉及大量变量和约束,导致解空间变得庞大和复杂,且存在多个局部最优解。因此,在寻找全局最优解的过程中,避免陷入局部最优解变得尤为关键,这增加了求解的难度。二是对计算资源需求高。这包括但不限于处理时间、内存容量和处理器性能。随着变量数量的增加,求解所需的时间可能会以指数级增长,这不仅对硬件设施提出了更高的要求,也对算法的优化提出了挑战。三是对解的精度要求高,小的误差可能会导致解的质量显著下降,最终影响结果的可靠性、有效性。
幸运的是,现实中的复杂应用场景通常是由最基础的低阶数学问题演化出来的。基础的数学问题通过不断组合和扩展,形成了复杂的应用场景。
比如,图像处理是从像素操作(基础矩阵运算)出发,发展出图像滤波、边缘检测等基本图像处理技术。在此基础上,运用基础卷积运算和激活函数,提取出图像高层次特征,使其能够处理复杂的图像分类、目标检测等任务,也构成了卷积神经网络(CNN)的基本框架。进一步,集成学习和深度学习技术通过多层网络结构和反向传播算法,结合多个学习器,大幅提升了模型的处理能力和预测精度,最终形成强大的图像处理与计算机视觉系统。
再举一个简单的例子,现实生活中的五颜六色,构成了丰富多彩的世界,但这么多阶的复杂颜色分类,其实都可以归结为最基础的“红黄蓝”三原色。通过三原色的多种组合,才演化出更高阶的、更细分的具象色彩。
由于高阶问题很复杂,所以直接求解非常困难,但降阶(二次化)可以将高阶函数转换为基础的二次函数,从而简化优化问题,使其更容易求解。
例如网络安全问题中的RSA加密算法的破解,借助降阶,用QUBO(二次无约束二值优化)可以建模整数分解问题,随着量子比特的增加,用量子计算破解RSA算法将更容易。此外,银行业务中通过设置信用评分卡的合理阈值,以使银行的最终收入最多的复杂问题,也能利用QUBO建模进行求解,得到高收益的银行卡设置方案。
面对不同行业场景下的实际问题的高阶函数,基于玻色量子自研的开物SDK都可以实现轻松降阶,将HOBO(高阶二值优化)通过添加约束条件转化为QUBO问题,简化问题难度,大幅加快解决NP-Hard组合优化问题的速度。
降阶思路:
HOBO可以通过添加约束条件转化为QUBO问题。
具体来说,即通过变量替换,令y=x0x1,将原式中的单项式阶数降低,并添加y=x0x1的约束。
银行信用评分卡设置的降阶案例
当大家借用充电宝的时候,都会显示一个信用评分的免押金弹窗,这是我们能看得见的一种信用等级评分。当我们在申请银行信用卡或相关的贷款等业务中,银行对客户授信之前,需要先通过各种审核规则对客户的信用等级进行评定,通过评定后的客户才能获得信用或贷款资格,这是我们看不见的一种信用等级评分。
在银行业,规则审核过程实际是经过一重或者多重组合规则后对客户进行打分,这些规则就被称为“信用评分卡”,每个信用评分卡又有多种阈值设置(有且只有一个阈值生效),这就使得不同的信用评分卡在不同的阈值下,对应不同的通过率和坏账率,一般通过率越高,坏账率也会越高,反之,通过率越低,坏账率也越低。
对银行来说,通过率越高,通过贷款资格审核的客户数量就越多,相应的银行获得的利息收入就会越多,但高通过率一般对应着高坏账率,而坏账意味着资金的损失风险,因此银行最终的收入可以定义为:
最终收入= 贷款利息收入-坏账损失
我们将该问题进行做如下简化:假设贷款资金为100万元,银行贷款利息收入率为8%,要为3种信用评分卡选取阈值。三种信用卡组合后,总通过率为所有信用卡的通过率相乘,坏账率为三种评分卡对应坏账率的平均值。也就是说,贷款利息收入=贷款资金×利息收入率×总通过率×(1-总坏账率)
那么,如何设置合理的阈值,使得最终收入最多?
实际上使用QUBO建模可以进行求解,得到高收益的银行卡设置方案。
设y1j,y2j,y3j 分别代表信用卡的第1、2、3种信用评分卡选择第j个阈值,选择则取1,不选则取0,h1j,h2j,h3j分别是第1、2、3种信用评分卡选择第j个阈值的坏账率。那么最终的收益率可以表达为:
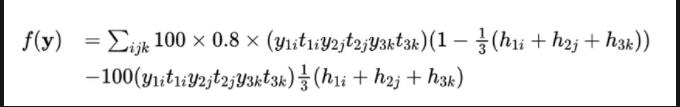
表达式中出现了高次项:y1iy2jy3k已经是三次项,需要借助降阶把它变成二次项。
设置辅助变量qij,用它替换公式中的y1iy2j并约束qij=y1iy2j。 借助新增的辅助变量和约束,原问题就转化为了二次问题。而要使得约束成立的方式是在原式中添加惩罚项,即Rosenberg二次惩罚项:
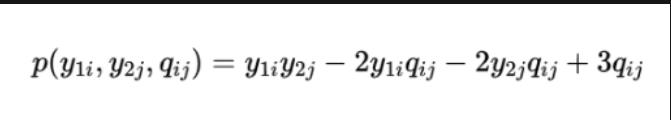
最终新的多项式为
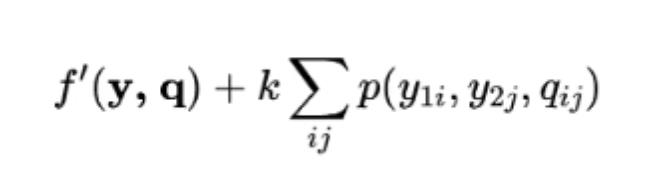
其中k是惩罚项系数。
其它降阶方法
对于特定的情况,也存在一些特殊的降阶方法。
如当某一高次项的系数为负数时,可以使用不同的二次化方法:
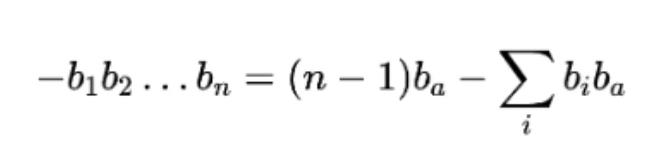
其中ba是辅助变量。
当b1b2...bn=1时,说明对所有的都满足bi=1,由于ba的取值只受b1,b2...bn影响,所以容易验证当ba取1时等式右侧QUBO值更低。当等式右侧取最低值时正好与等式左侧相等,取值为-1。
当b1b2...bn=0时,说明存在bi都满足bi=0,ba取1代入等式右侧得到
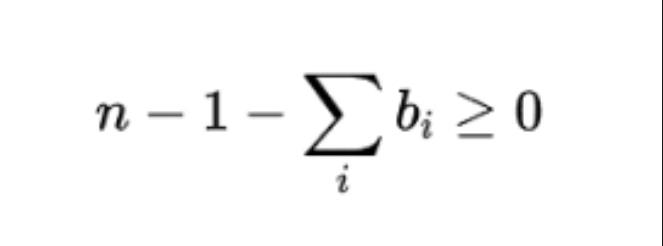
所以容易验证当ba取0时等式右侧QUBO值更低。当等式右侧取最低值时正好与等式左侧相等,取值为0。
举例:
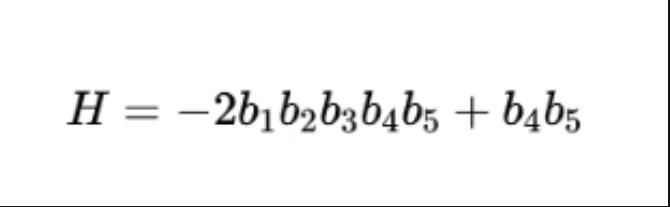
可以等价替换为:
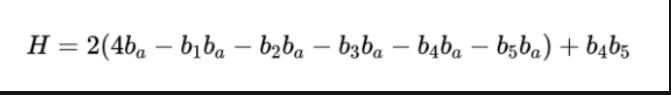
相比于上述方法,该方法可以用一个辅助变量将1个n次项变为2次,只增加1个辅助变量。但是应用范围要小。
针对不同的应用场景,还存在一些其它特定的降阶方法。
总结
对于现实生活中的不同行业不同场景下的复杂问题,高阶函数的降阶求解是一种通用型求解思维,基于玻色量子自研的开物SDK,用户只需关注建立与场景所对应的数学模型,SDK提供的方法可以自动完成降阶,用户不用关心背后的复杂度,大大降低用户使用相干光量子计算机求解问题的难度。
-
【量子计算机重构未来 | 阅读体验】+ 初识量子计算机2024-03-05 0
-
【量子计算机重构未来 | 阅读体验】+ 了解量子叠加原理2024-03-13 0
-
【《计算》阅读体验】量子计算2024-07-13 0
-
基于阿里云Serverless架构下函数计算的最新应用场景详解(一)2018-01-25 0
-
量子力学经典之固态物理应用2020-08-06 0
-
什么是高阶函数?2020-11-05 0
-
量子是个啥?量子计算机有啥用?2021-07-27 0
-
二阶有源滤波器的传输函数2010-05-23 19861
-
高阶滤波器的设计2010-05-23 7244
-
Labview之函数计算与绘图2016-04-19 609
-
玻色量子发布新一代550计算量子比特相干光量子计算机2024-04-19 531
-
量子计算场景实用秘籍:开物SDK之subQUBO算法分解2024-08-13 1202
全部0条评论

快来发表一下你的评论吧 !

