基于多传感器数据融合的漏磁信号采集与处理

随着电子技术、神经网络和人工智能处理技术的发展，国内外都在开展新的漏磁信号处理方法的研究。由于传统方法受人为因素影响严重，容易产生漏检误检，大大影响了检测准确度，因此特别需要一种对缺陷信号的智能化处理方法。多传感器数据融合技术是近年来形成和发展起来的一种自动化信息综合处理技术，它充分利用多源信息的互补性和计算机的高速运算能力来提高结果信息的质量。由于多传感器数据融合可以对来自多个传感器的数据进行多级别、多方面、多层次的处理，从而产生新的有意义的信息，而这种信息是任何单一传感器所无法获得的， 并且它还能有效地消除由于单一类型传感器失效而引起的误差，因而多传感器数据融合在信号处理领域得到了广泛的关注［1］。本文利用小波阈值降噪算法来突出信号缺陷特征，并将处理后的信号送入RBF神经网络数据融合中心，利用两类传感器之间的信息冗余来提高检测精度，消除测量中的不确定性，获得更准确可靠的测量结果。

数据融合传感器阵列

多传感器数据融合在运用过程的各阶段（例如模型建立、特征提取、目标识别等）需要各种各样的传感器。由于没有哪一类传感器的各种性能指标都绝对比其他类型传感器好，因此在一个系统中，需要同时采用多种类型的传感器，以提高系统检测、识别、分类和决策能力。本文根据系统的需要使用了两类传感器：电磁感应式传感器和霍尔传感器，利用它们之间产生的冗余信息进而检测出缺陷信号。

根据缺陷信号的特点以及环境要求，采用漏磁传感器阵列进行数据采集［2］。为提高检测灵敏度，减小钢管表面接触噪声和温度影响，由32个传感器组成的传感器阵列，贴敷在与钢管表面吻合的耐磨块内，形成探头。传感器被分为两组，每组16个。一组由16个电磁感应式传感器组成，另一组由16个霍尔传感器组成，两组交替分配在探头表面。传感器阵列传送出来的两组32路信号经过预处理之后被送到融合中心进行数据融合。

电磁感应式传感器

电磁感应式传感器的工作原理是：当它贴着钢管表面扫查时，钢管缺陷产生的漏磁场会引起穿过线圈的磁通量变化，从而使电磁线圈中产生感生电动势，形成缺陷信号。当检测用的电磁线圈与钢管做相对运动时，检测漏磁场的线圈所产生的感应电动势Uc为：

式中，n为线圈匝数，φ为线圈中通过的漏磁场磁通量；B为漏磁场的磁通量密度；S为线圈的横截面积，t为线圈运动时间。电磁感应式传感器能够在很大的温度范围中应用，且工作寿命长、抗灰尘、抗水和抗油污的能力强，即能耐受各种环境条件及外部噪声。

霍尔传感器

霍尔传感器检测漏磁信号的工作原理是：当电流I沿与磁场B的垂直方向通过时，在与电流和磁场垂直的霍尔传感器两侧便产生霍尔电势Hr：

式中，RH为霍尔系数；KH为霍尔系数RH与霍尔传感器厚度t之比，称为霍尔元件灵敏度。当霍尔系数RH与电流一定时，霍尔电势Hr只取决于磁场B的强度而与漏磁场的运动速度无关，因此，霍尔传感器不会受到管线检测的非匀速性的影响。

信号预处理

对于多传感器测量的漏磁缺陷信号数据，为了保证测试的准确性，系统取得信号之后，首先要对信号进行预处理，滤除各种外界干扰和各种噪声，获得正确的测量粗值。一般有两种方法：一是进行平滑处理，实际算法可通过滑动中值平滑器来实现;二是剔除粗大误差，可采取数据相关剔除法与信号平滑法同时进行，将来自多传感器具有相关性、互补性和冗余性的数据进行数据融合。这种方法可以充分利用被测目标在时间与空间上的信息，对被测量进行精确描述［4］。因此，多传感器融合的结果比单个传感器的测量值更为准确。

本文对漏磁缺陷信号使用小波降噪算法，该方法首先将每个传感器的测量值用小波阈值的方法去噪，以减小噪声对传感器测量值的影响。为了更好地重建传感器信号，可将各个传感器测量值进行归一化处理，然后再送入RBF神经网络的数据融合中心进行融合。对缺陷信号采取小波分析可以突出缺陷点，经过小波分析后可将缺陷信号的局部模极大值及其位置以及漏磁信号的波形特征等作为特征信息，用来区分不同的缺陷。

信号模型

在漏磁信号采集过程中，假设有N个传感器对同一缺陷的不同位置进行测量，每个传感器得到的漏磁信号测量值记为Xj（j=1，2，3.。.N），在测量过程中存在内部和外部噪声影响，测量值可以表示为：

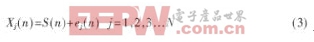
式中，S（n）为真实的被测量值，ej（n）（j=1，2，3.。.N）为第j个传感器在n时刻的加性噪声，Xj（n）为第j个传感器在n 时刻的实际测量值。由于每个传感器受到噪声干扰的程度不同，所以实际测量值偏离真实的被测量值的程度也是不同的。

小波阈值去噪

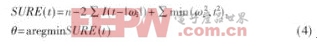
小波去噪的方法主要通过设置阈值来实现，对漏磁信号的离散小波变换，计算所有小波系数，剔除被认为与噪声有关的小波系数，然后通过小波变换的逆变换得到信号。对于给定的信号，选取阈值的方法很多，本文使用的是基于Stein无偏风险估计值最小化（SURE）的方法：

式中的阈值t，得到它的是似然函数，然后使似然函数最小化，得到所需阈值。在VISU的方法中阈值的选取固定不变，而在SURE方法中，阈值是自适应变化的，可以更好地降低噪声对缺陷信号的影响［4］。根据经过小波处理后的漏磁信号缺陷波形，可以提取出缺陷的特征向量，用以作为神经网络融合中心的输入。数据融合可根据融合的层次和实际内容将其分成像素层融合、特征层融合和决策层融合。本文把经过小波降噪处理后的信号通过RBF神经网络融合中心进行特征级融合，以对信号进行定量分析。

神经网络融合算法

常用的数据融合方法包括神经网络、聚类算法或模板法。其中，人工神经网络具有学习、记忆、联想、容错、并行处理等卓越功能，在拓扑结构、权重自适应等方面应用灵活，已在计量测试仪器标定、故障诊断中获得广泛应用。在多传感器测量系统中，采用数据融合技术可为系统带来多方面的益处［5］，如增强系统的稳定性、增加系统的可信度及提高系统的检测能力。由于BP神经网络收敛速度慢，网络训练时间较长，且存在局部极小值的问题，RBF神经网络比BP神经网络具有更快的学习特征，其逼近能力更强。因此，本系统选用RBF神经网络作为融合中心的特征层融合器进行融合训练。

神经网络结构

神经网络结构图如图2所示，第一层为输入层，用作特征信息融合信息采集，构成输入样本空间X；第二层为隐含层，用作将输入样本空间映射为高维的径向基函数空间，即对输入信息空间X进行特征提取。隐含层节点参数向量包括中心值Ci和标准偏差δi；第三层为输出层，ωi为第i个基函数与输出节点的连接权值，输出为Y，径向基函数选择高斯函数，如下：

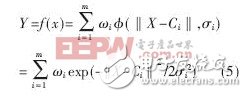
式中，m为隐含层节点数， ‖？‖为欧几里德范数。

神经网络学习过程分为两个阶段：第一阶段，根据所有的输入样本确定径向基函数及其参数，即确定隐含层各节点的高斯函数的中心值和标准偏差；第二阶段，在确定隐含层各参数后，根据样本，采用梯度下降算法，求出输出层的权值。

神经网络算法主要是通过调整连接权值，使输出层与期望输出逐渐趋于一致。根据最小均方差原理（MSE），当误差指标处于某一个范围之内时，则可以停止运算，表示网络训练成功。

神经RBF网络参数选取及权值更新

在融合中心，RBF神经网络的结构参数有径向基函数的隐含层节点数、中心值和标准偏差。节点数越多，学习能力越强，合理的节点数可通过训练得到最佳值。确定中心值和标准偏差可采用简单有效的聚类算法K-均值聚类算法。该方法具有实现简便、运算量较小、抗噪声能力强以及识别率高等优点，可以很好地解决建模样本分布不合理的问题。标准偏差的大小影响径向基函数对输入的响应，标准偏差太小则基函数只能对输入数据附近的很小区域做出响应，标准偏差过大则可能丢失固有的局部信息，模型精度也较差，因此标准偏差的选取应在一个稳定区间内进行。

本文利用梯度下降算法确定连接权值。假设总误差为：

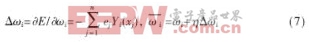
式中，p（xj）为第j个训练样本的期望输出；y（xj）为网络实际输出，n为训练样本总数。

式中，Yi（xj）为隐含层第i个基函数的输出； 为连接权值ωi的更新值；η为学习步长，一般为在0.2～0.9之间选取［7］。

实验仿真分析

本文采用MATLAB软件进行仿真实验，通过提供的40组人工裂缝的样本，对RBF神经网络系统进行训练学习和模式识别，并在学习初期对输入数据进行了预处理，通过样本训练逐渐生成最佳的RBF期网络［8］。另取10组测试样本数据作为输入，用MATLAB软件进行模拟仿真，同时利用RBF神经网络对其进行深度评估，并与常规BP神经网络进行对比。

仿真实验结果表明：利用RBF神经网络融合能比较精确地检测到信号缺陷深度，在学习能力和检测精度上，RBF神经网络均优于常规BP神经网络，该方法的平均绝对误差一般为2.69％，而常规BP神经网络的平均绝对误差为5.47％。可见，前者检测效果明显好于后者。

在漏磁缺陷信号中，利用小波降噪预处理可以在有效降低噪声影响的同时，最大程度上保留了缺陷的特征信息；采用漏磁传感器阵列，一定程度上克服了原有单传感器系统的检测误差；基于RBF神经网络的漏磁信号数据融合处理，可对裂纹深度检测的同时进行定量分析。实验结果表明，RBF 神经网络不仅具有很快的学习速度， 而且能够有效地提高检测的精度和准确率，消除信息的不确定性，提高传感器的可靠性。