

用有限元分析对圣维南原理进行探究
电子说
描述
基本上所有的结构工程师都会使用到圣维南原理。大多数结构力学教科书都收录了基于该原理的各种公式,但至今尚未对其进行严格证明。圣维南原理指出,只要载荷的合力正确,那么在远离载荷作用区的地方,载荷的精确分布就不重要。在本文中,我们将采用有限元分析对圣维南原理进行探究。
圣维南原理的历史
1855 年,法国科学家圣维南(Barré de Saint-Venant)发表了一个著名原理,但与其说这是一个严谨的数学命题,不如说是一个观察发现:
“如果作用在弹性体一小块表面上的力被作用于同一块表面上的静力等效力系替代,这种替换仅使局部表面产生显著的应力变化,而在比应力变化表面的线性尺寸更远的地方,其影响可忽略不计。”
B. Saint-Venant, Mém. savants étrangers, vol. 14, 1855.
圣维南肖像。图像来源于公有领域,通过 Wikimedia Commons 共享。
在应用力学领域,Boussinesq、Love、von Mises、Toupin 等科学家都对这一原理进行了精准的叙述,并给出了数学证明。但是对于很多一般性问题,论证圣维南原理具有很大难度,所以对该课题的研究仍在继续(有些论据相当鲜明)。
简单案例:远距离应力分析
让我们从一个简单的案例开始:对矩形薄板施加轴向拉力,与载荷作用边相隔一段距离处有一个圆孔。假如我们要分析孔的应力集中,那么实际的载荷分布有多重要呢?
我们对右侧边界施加了三种不同类型的载荷:
100 MPa 的恒定轴向应力
峰值振幅为 150 MPa 的对称抛物线应力分布
等于上述两种载荷工况合力的中心点载荷
如下方绘图所示,载荷施加方式不影响孔周围的应力分布。当然,关键在于孔距离载荷足够远。
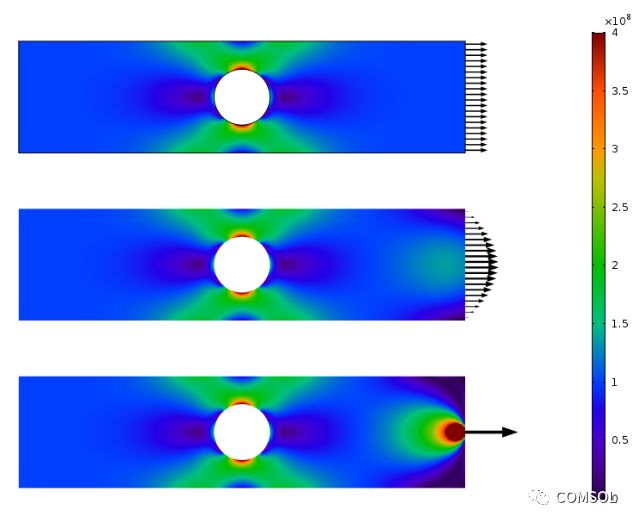
三种载荷工况对应的 Von Mises 应力分布。
该场景也可以使用箭头图来绘制主应力。此图将应力场绘制为通量,从而清晰地展示了应力重新分布的变化。
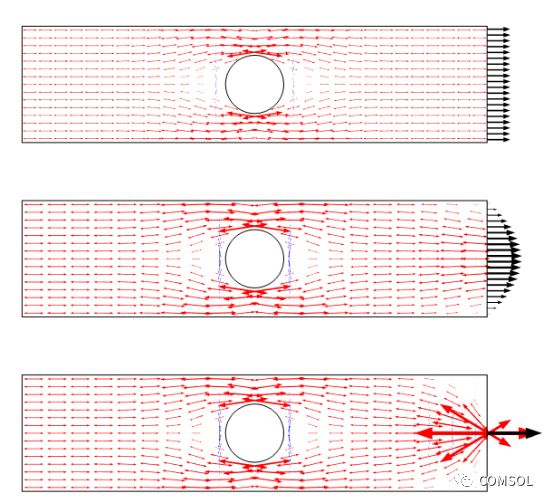
三种载荷工况的主应力绘图。请注意,使用点载荷时出现了一个奇异点。
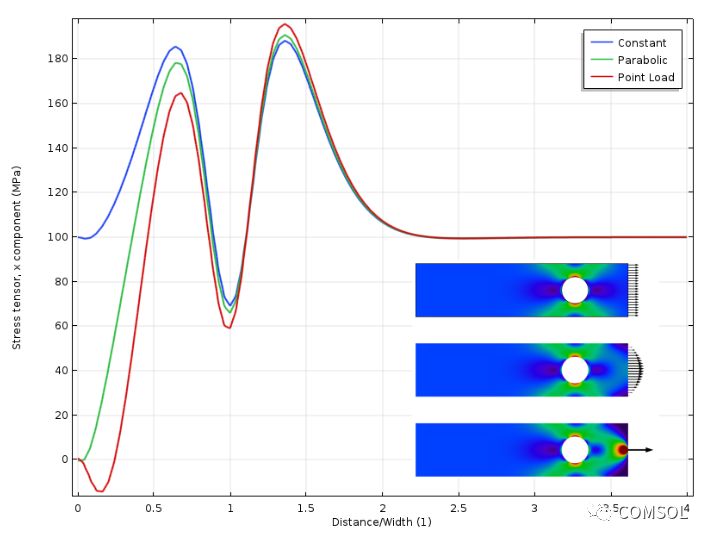
通过绘制应力曲线,我们发现当圆孔与受力边相距一定距离后,三种工况的曲线就会聚在一起,这个距离大约等于板的宽度。

顶边上的应力随与受力边界间距的变化而变化。距离为通过板宽进行标准化后的值。
如果孔向载荷作用边靠近,结果就会不同。这时,孔周围的应力状况取决于应力分布。更有意思的是,孔到三个应力场趋向一致的位置的距离是到载荷边界距离的两倍。应用圣维南原理的前提是应力可以自由地重新分布。然而在此例中,孔在一定程度上阻碍了应力重新分布。
孔离受力边更近时,顶边的应力分布。
值得注意的是,圣维南原理指出:当距离大约等于载荷作用区的线性尺寸量级时,应力状态没有差别。不过,要考虑的受载区却未必是真正加载的地方!这个说法听起来或许很奇怪,我们可以这样想:当孔距离较远时,我们可根据参考书(我的参考书为 4.32),而不是使用有限元解来计算应力集中系数。参考书中有一个隐含假设:在第一个载荷工况中,载荷是均匀分布的。因此,即便载荷实际上只施加到一小块边界上,该例中的临界距离仍与整个边界尺寸都有关。
如果使用有限元方法(FEM)来求解问题,孔可以任意接近载荷。唯一的限制是,从物理的角度来看,载荷分布是明确定义的。不过,只要我们对重新分布做出假设,就会存在关于载荷分布的隐含假设,而这个假设可能与实际情况不同。
零力系与应变能密度
我们在上文中解释了在特定的适当距离之外,应力大小,其大小与载荷大小无关。因此,在处理线弹性时,我们总是可以叠加载荷工况。当证明圣维南原理时,很容易沿着这个思路总结出一个原则:由无合力或力矩的载荷系统引起的应力在一定距离之外很小,该距离与载荷作用边界的尺寸是同一数量级。
所以,我们将对两个合力相同的载荷系统的差别所导致的应力进行研究。近代的大多数证明都以这类零力系的应变能密度的衰减的估计值为基础。
回到上面的问题,我们可以计算各个载荷工况的差别,借此对由应力场的差别造成的应力或应变能密度的衰减现象进行准确的研究。

合力为零的载荷工况的应变能密度的对数。

合力为零的载荷工况对应的薄板应变能密度。为了使能量仅仅取决于与载荷的距离而变化,对垂直方向的能量进行了积分。
应变能密度的对数衰减率与同载荷作用边界的距离或多或少呈线性关系。这实际上符合现代证明的预测——应变能密度的指数衰减。我们还能清晰地看到圆孔是如何短暂降低衰减率的。
对薄壁结构应用圣维南原理
众所周知,对于壳体、梁和桁架之类的薄壁结构,我们不能按处理“结实”物体的方式来应用圣维南原理。因为薄壁结构内的载荷路径少得多,所以扰动传播的距离比想象中远。上文的圆孔案例也出现了这种现象,只是薄壁结构更加显著。
在本文中,我们选择研究一个符合 IPE100 截面标准的梁。梁末端受到轴向应力的作用,应力大小在两个横截面方向均呈线性分布。

使用等值线和箭头来表示载荷分布。
由于载荷具有对称性,因此其合力为零,所有轴线周围的力矩也为零。横截面高 100 mm,如果圣维南原理的标准形式对其适用,那么在距离末端截面约 100 mm 的地方应力应该很小。

梁内的有效应力。红色等值线表示低于施加的峰值应力的 5% 的应力。
事实证明,为了使应力低于施加的峰值应力的 5%,应力必须沿梁移动近一米的距离,而上翼缘和下翼缘需要通过薄腹板传递力矩来保持平衡,这就造成应力重新分布的效率非常低。
如果你十分熟悉梁的非均匀扭转理论,比如翘曲理论或弗拉索夫理论,就会意识到施加的载荷有很大的双力矩。双力矩是一个横截面量,其物理大小等于力 X 长度 2。
或许在此例中(只是我个人的推测),圣维南原理有效的条件不仅是力和力矩为零,还有双力矩为零。这一点可以通过增加四个可抵消双力矩的点载荷来实现。该分析的结果如下图所示。

绘图显示了添加了四个点载荷,双力矩变为零后的有效应力。现在 5% 的应力等值线十分靠近载荷作用边界。
我们没有特意选择施加点载荷的最优位置,点载荷产生了极大的(实际为奇异的)局部应力。不过,应力很快下降,超出 100 mm 左右后都小于 5%。5% 的下限仍然是针对所施加的分布载荷而言,并没有根据新的局部应力进行调整。增加点载荷之后,应变能密度的对数衰减率加快了两倍。
有限元分析中的圣维南原理
很多情况下,你可以直观地认为圣维南原理适用于有限元离散化问题。在本文中,我们主要探讨分布载荷和不相容网格。
分布载荷
虽然我们在有限元模型中将应力设为连续的边界载荷,但总要将应力施加在网格节点上。如下方案例所示,根据虚功原理载荷分布到单元内部节点。
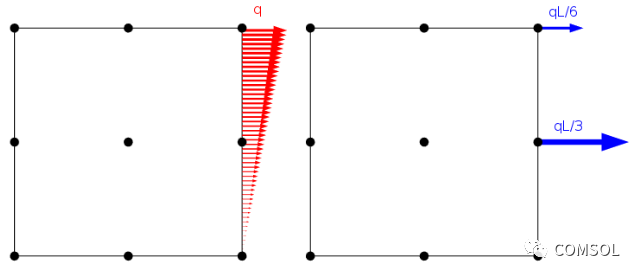
线性分布载荷以及如何将其施加在边长为 L 的二阶拉格朗日单元节点上。
不过,只要合力和力矩相同,相同的节点载荷可以对应无数种载荷分布。显然,这类情况的有限元问题都拥有相同的解。不过,我们可以根据圣维南原理推断,只要相距一定距离,这类载荷本质上应该产生相同的应力场。
由于载荷重新分布的区域尺寸是基于单元面的,因此线性尺寸本质上是结构内部的一个单元层。所以,单元最外层的解可能与实际载荷不符,内部的解则相同。
举个例子,我们对一块矩形板施加了应力呈指数分布的边界载荷,并采用细化网格进行了计算,应力结果如下图所示。

轴向应力分布的等值线图。
不出所料,受圣维南原理的影响,在离载荷作用边一定距离的地方,应力场重新分布成了纯弯曲状态。不过,这不是本次讨论的核心。我们研究的是上方的应力分布与使用粗化网格得到的应力分布之间的差别。
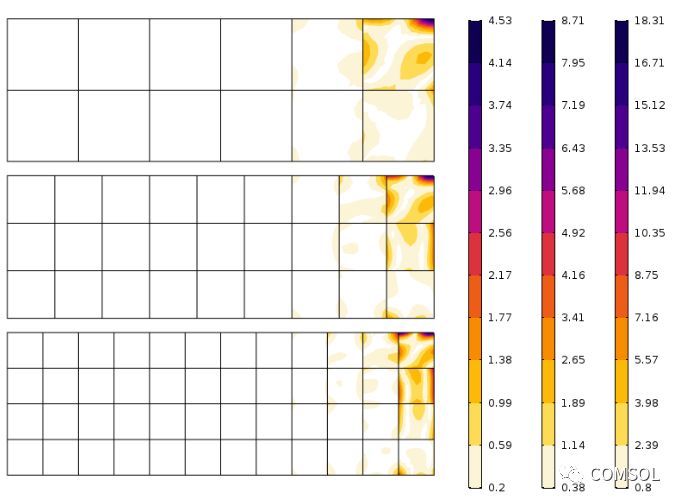
采用三种不同网格对应的轴向应力误差。注意三者尺度不同。网格越细,误差越小,这符合预期。
可以发现,经过第一个单元层之后,误差快速减少。图中实际上是网格的收敛性和符合圣维南原理的应力重新分布的共同效果。
不相容网格
当两个相互连接的单元的形函数不匹配时,会出现不相容网格。这类问题最常见于使用一致对和连续性条件来连接装配的情况。为了举例说明,我们选择对一根包含故意不匹配的网格的直杆进行研究。通过施加简单的载荷工况,比如单轴拉伸,我们就能研究由过渡导致的应力扰动。

不相容网格过渡处的轴向应力。图片使用了二阶单元。
左右两侧的节点传递的力并不符合应力不变的假设。这种情况也可以被看作局部载荷在等于单元大小的区域上进行重新分布。根据圣维南原理,我们推断在“单元大小”的距离之外,扰动会逐渐消失。下面我们研究一下轴向网格细化后,将会出现什么情况。

应力误差大于 0.1% 的区域。在轴向上使用了三种不同的离散化。
结果证明,扰动区域在垂直于过渡边界的方向上不受离散化的影响。这与圣维南原理的推断完全一致。
结束语
因为不可知详细的载荷分布,所以如果不使用圣维南原理,很多结构分析都难以进行。
在形式上,原理只对线弹性材料有效。在实践中,我们每天也会直觉地将其应用于其他类型的仿真。举例来说,如果“带孔板”案例中的材料是弹塑性的,只要屈服应力大于边界应力,且孔周围只有弹性变形,我们就会预测两个分布载荷生成相同的结果。不过,因为点载荷周围的材料发生了屈服,所以点载荷总是生成不同的解。
-
有限元分析2008-06-17 0
-
MATLAB有限元分析与应用2011-02-28 0
-
如何有效的学习CAE有限元分析2020-07-07 0
-
求一种有限元分析中PCBA的简化建模方法2021-04-19 0
-
全美经典丛书-有限元分析2008-09-06 858
-
有限元分析及应用_曾攀2011-05-02 1932
-
有限元分析讲座2011-05-06 580
-
abaqus动力学有限元分析指南2016-05-11 1237
-
采用环梁加固风机基础的有限元分析2017-01-02 775
-
基于Ansoft的开关磁阻电机有限元分析与研究2017-01-21 1006
-
两相开关磁阻电机磁场二维有限元分析2017-01-21 646
-
Ansoft工程电磁场有限元分析2017-04-01 1594
-
有限元分析相关知识的解析2017-11-12 1194
-
基于箱形梁CADCAE有限元分析2021-07-26 682
-
动力学有限元分析教程下载2021-12-06 711
全部0条评论

快来发表一下你的评论吧 !

