带你入门SVM,从较高的层次讲解SVM的机制

编者按：无需艰深的数学，[24]7.ai首席数据科学家Abhishek Ghose带你入门SVM（支持向量机）。

如果你曾经使用机器学习解决分类问题，你可能听说过支持向量机（SVM）。五十年来，SVM随着时间而演化，并在分类之外得到应用，例如回归、离散值分析、排序。

SVM是许多机器学习从业者军火库中的最爱。在247.ai，我们同样使用SVM解决各种各样的问题。

本文将试图从较高的层次讲解SVM的机制。我将聚焦于发展直觉而不是严谨的细节。这意味着我们将跳过尽可能多的数学，发展对SVM工作原则的强有力的直觉。

分类问题

假设你的大学开设了一门机器学习（ML）课程。课程导师发现数学或统计学好的学生表现最佳。随着时间的推移，积累了一些数据，包括参加课程的学生的数学成绩和统计学成绩，以及在ML课程上的表现（使用两个标签描述，“优”、“差”）。

现在，课程导师想要判定数学、统计学分数和ML课程表现之间的关系。也许，基于这一发现，可以指定参加课程的前提条件。

这一问题如何求解？让我们从表示已有数据开始。我们可以绘制一张二维图形，其中一根轴表示数学成绩，另一根表示统计学成绩。这样每个学生就成了图上的一个点。

点的颜色——绿或红——表示学生在ML课程上的词表现：“优”或“差”。

当一名学生申请加入课程时，会被要求提供数学成绩和统计学成绩。基于现有的数据，可以对学生在ML课程上的表现进行有根据的猜测。

基本上我们想要的是某种“算法”，接受“评分元组”(math_score, stats_score)输入，预测学生在图中是红点还是绿点（绿/红也称为分类或标签）。当然，这一算法某种程度上包括了已有数据中的模式，已有数据也称为训练数据。

在这个例子中，找到一条红聚类和绿聚类之间的直线，然后判断成绩元组位于线的哪一边，是一个好算法。

这里的直线是我们的分界（separating boundary）（因为它分离了标签）或者分类器（classifier）（我们使用它分类数据点）。上图显示了两种可能的分类器。

好 vs 差的分类器

这里有一个有趣的问题：上面的两条线都分开了红色聚类和绿色聚类。是否有很好的理由选择一条，不选择另一条呢？

别忘了，分类器的价值不在于它多么擅长分离训练数据。我们最终想要用它分类未见数据点（称为测试数据）。因此，我们想要选择一条捕捉了训练集中的通用模式（general pattern）的线，这样的线在测试集上表现出色的几率很大。

上面的第一条线看起来有点“歪斜”。下半部分看起来太接近红聚类，而上半部分则过于接近绿聚类。是的，它完美地分割了训练数据，但是如果它看到略微远离其聚类的测试数据点，它很有可能会弄错标签。

第二条线没有这个问题。

我们来看一个例子。下图中两个方形的测试数据点，两条线分配了不同的标签。显然，第二条线的分类更合理。

第二条线在正确分割训练数据的前提下，尽可能地同时远离两个聚类。保持在两个聚类的正中间，让第二条线的“风险”更小，为每个分类的数据分布留出了一些摇动的空间，因而能在测试集上取得更好的概括性。

SVM试图找到第二条线。上面我们通过可视化方法挑选了更好的分类器，但我们需要更准确一点地定义其中的理念，以便在一般情形下加以应用。下面是一个简化版本的SVM：

找到正确分类训练数据的一组直线。

在找到的所有直线中，选择那条离最接近的数据点距离最远的直线。

距离最接近的数据点称为支持向量（support vector）。支持向量定义的沿着分隔线的区域称为间隔（margin）。

下图显示了之前的第二条线，以及相应的支持向量（黑边数据点）和间隔（阴影区域）。

尽管上图显示的是直线和二维数据，SVM实际上适用于任何维度；在不同维度下，SVM寻找类似二维直线的东西。

例如，在三维情形下，SVM寻找一个平面（plane），而在更高维度下，SVM寻找一个超平面（hyperplane）——二维直线和三维平面在任意维度上的推广。这也正是支持向量得名的由来。在高维下，数据点是多维向量，间隔的边界也是超平面。支持向量位于间隔的边缘，“支撑”起间隔边界超平面。

可以被一条直线（更一般的，一个超平面）分割的数据称为线性可分（linearly separable）数据。超平面起到线性分类器（linear classifier）的作用。

允许误差

在上一节中，我们查看的是简单的情形，完美的线性可分数据。然而，现实世界通常是乱糟糟的。你几乎总是会碰到一些线性分类器无法正确分类的实例。

下图就是一个例子。

显然，如果我们使用一个线性分类器，我们将永远不能完美地分割数据点。我们同样不想干脆抛弃线性分类器，因为除了一些出轨数据点，线性分类器确实看起来很适合这个问题。

SVM允许我们通过参数C指定愿意接受多少误差。C让我们可以指定以下两者的折衷：

较宽的间隔。

正确分类训练数据。C值较高，意味着训练数据上容许的误差较少。

再重复一下，这是一个折衷。以间隔的宽度为代价得到训练数据上更好的分类。

下图展示了随着C值的增加，分类器和间隔的变化（图中没有画出支持向量）：

上图中，随着C值的增加，分割线逐渐“翘起”。在高C值下，分割线试图容纳右下角大部分的红点。这大概不是我们想要的结果。而C=0.01的图像看起来更好的捕捉了一般的趋势，尽管和高C值情形相比，他在训练数据上的精确度较低。

同时，别忘了这是折衷，注意间隔是如何随着C值的增加而收窄的。

在上一节的例子中，间隔曾经是数据点的“无人区”。正如我们所见，这里再也无法同时得到良好的分割边界和相应的不包含数据点的间隔。总有一些数据点蔓延到了间隔地带。

由于现实世界的数据几乎从来都不是整洁的，因此决定较优的C值很重要。我们通常使用交叉验证（cross-validation）之类的技术选定较优的C值。

非线性可分数据

我们已经看到，支持向量机有条不紊地处理完美线性可分或基本上线性可分的数据。但是，如果数据完全线性不可分，SVM的表现如何呢？毕竟，很多现实世界数据是线性不可分的。当然，寻找超平面没法奏效了。这看起来可不妙，因为SVM很擅长找超平面。

下面是一个非线性可分数据的例子（这是知名的XOR数据集的一个变体），其中的斜线是SVM找到的线性分类器：

显然这结果不能让人满意。我们需要做得更好。

注意，关键的地方来了！我们已经有了一项非常擅长寻找超平面的技术，但是我们的数据却是非线性可分的。所以我们该怎么办？将数据投影到一个线性可分的空间，然后在那个空间寻找超平面！

下面我们将逐步讲解这一想法。

我们将上图中的数据投影到一个三维空间：

下面是投影到三维空间的数据。你是不是看到了一个可以悄悄放入一个平面的地方？

让我们在其上运行SVM：

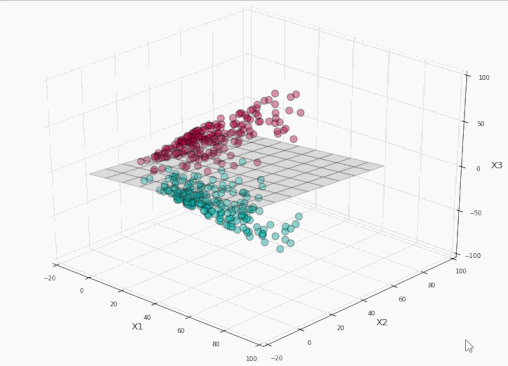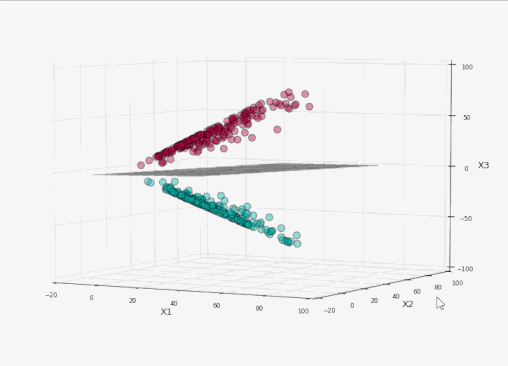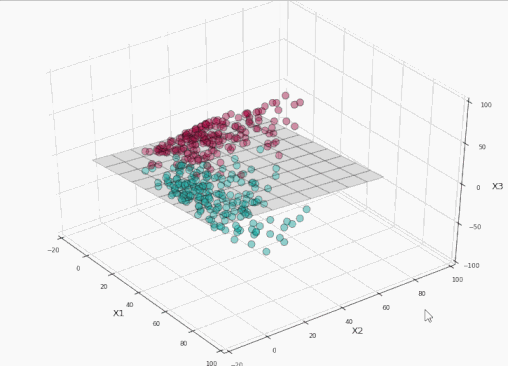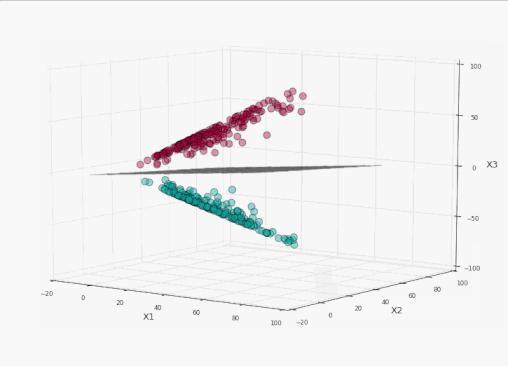
太棒了！我们完美地分割了标签！现在让我们将这个平面投影到原本的二维空间：

训练集上精确度100%，同时没有过于接近数据！耶！

原空间的分割边界的形状由投影决定。在投影空间中，分割边界总是一个超平面。

别忘了，投影数据的主要目标是为了利用SVM寻找超平面的强大能力。

映射回原始空间后，分割边界不再是线性的了。不过，我们关于线性分割、间隔、支持向量的直觉在投影空间仍然成立。

我们可以看到，在左侧的投影空间中，三维的间隔是超平面之上的平面和之下的平面中间的区域（为了避免影响视觉效果，没有加上阴影），总共有4个支持向量，分别位于标识间隔的上平面和下平面。

而在右侧的原始空间中，分割边界和间隔都不再是线性的了。支持向量仍然在间隔的边缘，但单从原始空间的二维情形来看，支持向量好像缺了几个。

现在让我们回过头去分析下发生了什么？

1. 如何知道应该把数据投影到哪个空间？

看起来我找了一个非常特定的解——其中甚至还有√2。

上面我是为了展示投影到高维空间是如何工作的，所以选择了一个特定的投影。一般而言，很难找到这样的特定投影。不过，感谢Cover定理，我们确实知道，投影到高维空间后，数据更可能线性可分。

在实践中，我们将尝试一些高维投影，看看能否奏效。实际上，我们可以将数据投影到无穷（infinite）维，通常而言效果很好。具体细节请看下一节。

2. 所以我首先投影数据接着运行SVM？

否。为了让上面的例子易于理解，我首先投影了数据。其实你只需让SVM为你投影数据。这带来了一些优势，包括SVM将使用一种称为核（kernels）的东西进行投影，这相当迅速（我们很快将讲解原因）。

另外，还记得我在上一点提过投影至无穷维么？那该如何表示、存储无穷维呢？结果SVM在这一点上非常聪明，同样，这和核有关。

现在是时候查看下核了。

核

这是让SVM奏效的秘密武器。这里我们需要一点数学。

让我们回顾下之前的内容：

SVM在线性可分的数据上效果极为出色。

使用正确的C值，SVM在基本线性可分的数据上效果相当出色。

线性不可分的数据可以投影至完美线性可分或基本线性可分的空间，从而将问题转化为1或2.

看起来让SVM得到普遍应用的关键是投影到高维。这正是核的用武之地。

SVM优化

之前我们略过了SVM寻找超平面的数学部分，现在为了更好地说明核的作用，我们需要还下之前的欠债。

假设训练数据集包含n个数据点，其中每个数据点用一个元组表示(xi, yi)，其中xi为表示数据点的向量，yi为数据点的分类/标签（不妨令yi的取值为-1或1）。那么，分割超平面就可以表示为：

wx - b = 0

其中，w为超平面的法向量。

将某一数据点xi代入wx - b后，根据所得结果的正负，就可以判断数据点的分类。

相应地，确定间隔的两个超平面则可以表示为

wx - b = 1 wx - b = -1

这两个超平面之间的距离，也就是间隔的宽度为2/||w||

SVM的目标是在正确分类的前提下，最大化间隔宽度，也就是说，在满足yi(wxi - b) >= 1的前提下，最大化2/||w||，也就是最小化||w||。

上式中，i = 1, …, n，也就是说，所有数据点都要满足。但实际上，并不需要为所有数据点进行计算，只需要为所有支持向量计算即可。另外，上式中，我们乘上了yi（取值为1或-1），这就同时保证了间隔两侧的数据点都符合要求。

下面我们需要使用一些更深入的数学。显然，最小化||w||等价于最小化

这一变换表明这是一个二次优化问题，有成熟的方案可以使用。

不过，通过拉格朗日对偶（Lagrange Duality）变换，可以进一步将其转换为对偶变量（dual variable）优化问题：

加入拉格朗日乘数

然后可以找出更高效的求解方法：（这里略去具体推导过程）

另外，在推导过程中，我们得到了一个中间结果，w可以通过下式计算：

你可以不用在意以上公式的细节，只需注意一点，以上计算都是基于向量的内积。也就是说，无论是超平面的选取，还是确定超平面后分类测试数据点，都只需要计算向量的内积。

核函数

而核函数（kernel function），简称核（kernel）正是算内积的！核函数接受原始空间中两个数据点作为输入，可以直接给出投影空间中的点积。

让我们回顾下上一节的例子，看看相应的核函数。我们同时也将跟踪投影和内积的运算量，以便和核函数对比。

给定数据点i：

相应的投影为：

算下得到投影需要的运算量：

计算第一维：1次乘法

计算第二维：1次乘法

计算第三维：2次乘法

共计1+1+2 = 4次乘法

同理，数据点j投影也需要4次乘法。

数据点i和数据点j在投影空间的内积为：

内积计算需要3次乘法、2次加法。

也就是：

乘法：8（投影）+ 3（内积） = 11

加法：2（内积）

共计11 + 2 = 13次运算

而以下核函数将给出相同结果：

以上核函数在原始空间计算内积，然后取平方，直接得到结果。

只需展开以上公式就可以验证结果是一致的：

需要几次运算？在二维情形下计算内积需要2次乘法、1次加法，然后平方又是1次乘法。所以总共是4次运算，仅仅是之前先投影后计算的运算量的31%。

看来用核函数计算所需内积要快得多。在这个例子中，这点提升可能不算什么：4次运算和13次运算。然而，如果数据点有许多维度，投影空间的维度更高，在大型数据集上，核函数节省的算力将飞速累积。这是核函数的巨大优势。

大多数SVM库内置了流行的核函数，比如多项式（Polynomial）、径向基函数（Radial Basis Function，RBF）、Sigmoid。当我们不进行投影时（比如本文的第一个例子），我们直接在原始空间计算点积——我们把这叫做使用线性核（linear kernel）。

许多核函数提供了微调的选项，比如，多项式核函数：

让你可以选择c和d的值。在上面的三维投影问题中，我使用的就是c=0、d=2的多项式核函数。

不过我们还没有说完核函数的酷炫之处呢！

还记得我之前提过投影至无穷维？你应该已经猜到了吧，这需要正确的核函数。只需找到正确的核函数，我们就可以计算所需内积，并不用真的投影输入数据，也不用操心存储无穷维度。

RBF核就常常用于特定的无穷维投影。我们这里就不介绍相关的数学了，如果你想深入数学，可以参考文章底部给出的资源。

你也许会纳闷，我们如何能够计算无穷维上的点积？如果你为此困惑，可以想想无穷级数求和。

我们已经回答了上一节提出的问题。总结一下：

我们通常并不定义数据的投影。相反，我们从现有的核中选取一个，加以微调，以找到最匹配数据的核函数。

我们当然可以定义自己的核，甚至自行投影。但许多情形下不必如此。至少，我们从尝试现有核函数开始。

如果存在我们想要的投影的核，我们将使用它，因为核经常快很多。

RBF核可以投影数据点至无穷维。

SVM库

你可以从以下SVM库开始上手：

libSVM

SVM-Light

SVMTorch

scikit-learn之类的许多通用ML库也提供了SVM模块，这些模块常常是专门SVM库的封装。我建议从久经考验的libSVM开始。

libSVM可以作为命令行工具使用，也提供了Python、Java、Matlab封装。只要你的数据文件的格式可以被libSVM理解（详见README），你就可以开始使用了。

事实上，如果你需要快速了解不同核、C值等对寻找分割边界的影响，你可以尝试libSVM主页上的“图形界面”。标记数据点分类，选择SVM参数，然后点击运行（Run）！

这个可视化工具的魅力无可阻挡，下面是我标记的一些数据点：

没错，我要给SVM一点难度。

接着我尝试了一些核：

这个可视化工具不显示分割边界，但会显示SVM学习的属于某一特定标签的区域。如你所见，线性核完全忽略了红点。它认为整个空间是黄色的（更准确地说，黄绿色）。而RBF核干净利落地为红点划出了一个圈。

有帮助的资源

本文主要依靠可视化的直观理解。虽然这是很棒的初步理解概念的方式，我仍然强烈建议你深入一点。毕竟有些地方可视化的直观理解是不够的。其中一些概念用于决定折衷优化，除非你查看数学，否则很难直观地理解一些结果。

另外，数学也有助于理解核函数。例如，本文对RBF核的介绍一笔带过。我希望它的“神秘”——和无穷维投影的关系，以及最后数据集上奇妙的结果（“圈”）——能让你想要更深入地了解它。

推荐的资源

视频讲座：Learning from Data —— Yaser Abu-Mostafa的第14讲至第16讲讨论了SVM以及核函数。如果你正在找ML的入门讲座，我强烈推荐整个系列，它在数学性和直观性上平衡得很好。

书籍：统计学习基础 —— Trevor Hastie、Robert Tibshirani、Jerome Friedman著。第4章介绍了SVM背后的基本想法，而第12章全面讨论了SVM的细节。

快乐（机器）学习！