

不对称半桥变压器直流偏磁的产生原因及如何解决
描述
引 言
不对称半桥具有结构简单,控制方便和无需辅助器件就可以实现软开关等优点,所以在中小功率的应用场合很有优势。但是这种不对称的控制方法却导致变换器中的隔离变压器励磁电流具有直流分量。这就要求变压器必须有足够能力承受直流偏磁,通常对于铁氧体磁芯要开一定的气隙以防止饱和。但是变压器开气隙,会令变压器的励磁电感减小,从而增加励磁电流和损耗。
本文详细分析了不对称半桥变压器直流偏磁的产生机理,并且探讨了两种解决偏磁问题的方法。
1 不对称半桥结构分析
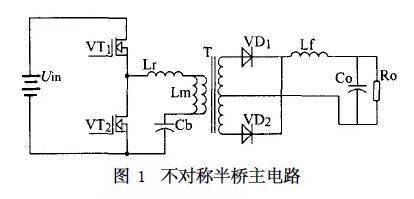
传统的半桥采用两路相位相差180°,脉冲宽度相同的驱动信号分别驱动上下两个开关管。不对称半桥并没有改变传统半桥的主威廉希尔官方网站 结构,而是采用两路互补的驱动信号分别驱动开关管。当一个开关的占空比为D ,则另外一个开关管占空比为1 - D(忽略死区时间) 。这样利用变压器的漏感或者串联谐振电感可以实现两个开关管的零电压开通。图1为不对称半桥的主威廉希尔官方网站 结构。Lr 为谐振电感, Lm为变压器原边励磁电感,Lf 为输出滤波电感, T为理想变压器。
在电流连续模式下,输入输出电压关系为:
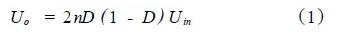
这里n = ns / np 为次级绕组和初级绕组的比值,如果次级采用平衡绕组,则两个次级绕组和初级绕组的比值为n1 = n2 = n。从式(1)中可知,当占空比D = 0. 5的时候, Uo 最大。所以通常把D 限制在《0. 5或者》 0. 5。
2 变压器直流偏磁机理分析
对于对称半桥,在稳态工作条件下,变压器是双向对称磁化的。也就是,励磁电流没有直流分量。所以,对称半桥的变压器无需开气隙。但是,不对称控制下的半桥变压器的励磁电流具有直流分量,而且与两个开关管占空比的不对称度和输出电流有关。
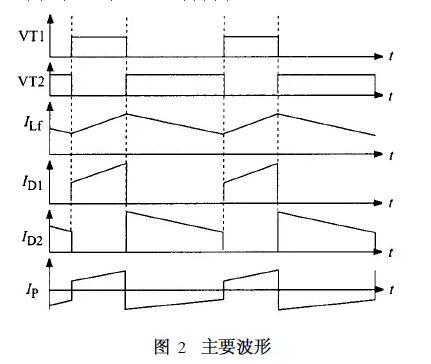
图2为两个开关管VT1和VT2的驱动波形(忽略死区) 、次级滤波电感的电流波形、两个整流二极管的电流波形以及理想变压器的原边电流。VT1和VT2的占空比分别为D 和12D。电感电流的平均值为输出电流Io。两个整流管的电流ID1和ID2 ,也就是两个变压器次级的输出电流,分别在其占空时间D和12D中,平均值也为Io。依据理想变压器的电流关系,可以得到理想变压器原边电流Ip。从其波形中可以得知, Ip 具有直流分量。而对于半桥威廉希尔官方网站 ,变压器原边串了一个电容Cb。在稳态工作情况下,只有交流电流能通过Cb ,从而励磁电感Lm 上电流Im 也必然会有直流分量,其值为
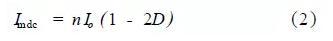
从式(2)可以看出, Imdc与Io 和D 有关,当D 等于0. 5的时候Imdc = 0;当D等于0和1的时候Imdc达到最大。
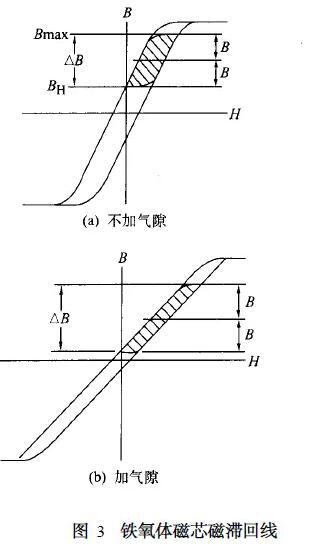
通常开关电源变压器多采用铁氧体磁芯。铁氧体磁芯虽然磁导率高,但是饱和磁密低,所以承受直流偏磁能力很弱。图3为铁氧体磁芯不加气隙和加气隙的磁滞回线。
对于磁化强度:

所以从图3可以看到不加气隙的铁氧体磁芯能承受的直流电流非常小,所以只有采取加气隙的方式来解决这个问题。但是气隙会导致励磁电流增加,降低了变压器的利用率,不利于减小变压器体积和提高效率。
3 解决方法
(1)不对称绕组解决偏磁问题
对于对称绕组的不对称半桥,只有在D = 0. 5的时候,变压器才不会出现直流偏磁。然而实际情况中,让变换器工作在D = 0. 5是不可能的。采用不对称绕组,也就是两个次级相对于初级的变比不同。假设一个为n1 ,另外一个为n2 ,则变压器励磁电流直流分量为:

(2)次级倍流整流解决偏磁问题
除了采用次级不对称绕组之外,还可以采用次级倍流整流的方式来解决偏磁问题。图4为倍流整流的不对称半桥主威廉希尔官方网站 。该电流次级采用两个滤波电感L1 和L2 ,比较适合大电流输出的场合。
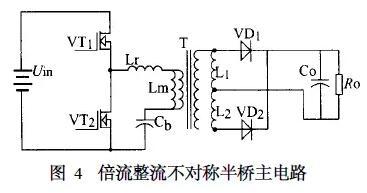
对于次级倍流整流的不对称半桥的输出电压为:
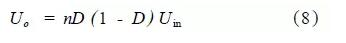
这里n为变压器次级和初级的匝比。若整流电感L1 和L2 的平均电流分别是IL1和IL2 ,则变压器次级输出电流的平均值为:

而对于电感L1 和L2 ,两者的平均电流是根据其等效串联电阻RL1和RL2分配的:

把式(10)代入式(11) ,得到
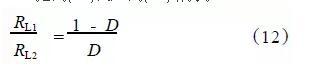
也就是说满足式(12 )就可以消除变压器的直流偏磁。
4 仿真分析
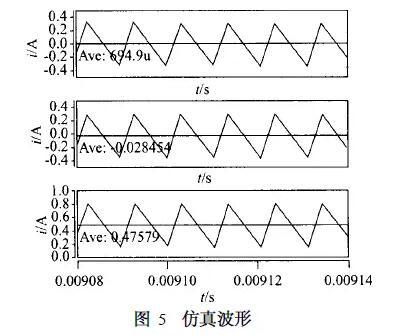
利用仿真软件saber对三种威廉希尔官方网站 分别做仿真。输入电压为300 V,输出电压为15 V,输出电流为10A。占空比D = 0. 3。图5为仿真后变压器原边励磁
电感的电流,分别为:次级对称绕组n = 1 /8, Imdc =456 mA;次级不对称绕组n1 = 1 /6, n2 = 1 /14 Imdc =28. 5 mA;次级倍流整流: n = 1 /4, RL1 = 0. 07Ω, RL2= 0. 03Ω, Imdc = 0. 69 mA。
5 结 论
传统不对称半桥的变压器因为有直流偏磁,所以变压器的利用率不高。本文从理论上分析了直流偏磁产生的原因,并且探讨了次级不对称绕组和次级倍流整流这两种方法来解决偏磁问题。最后通过仿真验证了两种方法的可行性。
-
不对称半桥变换器讲义2019-05-01 0
-
不对称半桥属于降压还是升压变换器2020-04-13 0
-
不对称半桥变换器中的高频变压器设计公式2023-09-19 0
-
采用磁集成技术的不对称半桥倍流整流变换器2009-09-07 567
-
基于不对称半桥的单级不对称半桥变换器2009-10-14 860
-
了一种基于不对称半桥的单级不对称半桥变换器2009-10-17 703
-
不对称半桥DC DC变换器2009-10-17 636
-
采用不对称绕组变压器的不对称半桥威廉希尔官方网站 的研究2009-10-19 1036
-
变压器的不对称运行及瞬态过程2009-11-17 354
-
不对称半桥式正激变流器威廉希尔官方网站2008-08-22 2289
-
不对称半桥变换器的研究2009-07-07 3177
-
采用不对称绕组变压器的不对称半桥威廉希尔官方网站 的研究及原理2017-09-14 1128
-
【资料】【下载】不对称半桥变换器的CCM等效电源平均威廉希尔官方网站 模型2017-12-19 952
-
不对称半桥变换器的CCM小信号传递函数2021-05-29 775
-
直流偏磁变压器建模2021-09-27 795
全部0条评论

快来发表一下你的评论吧 !

