RCD吸收计算结果为何与实际差别大？

网上有很多关于RCD钳位吸收计算的技术文章和观点，但很多人发现计算出的数值和实验得到的参数并不一样。相信很多工程师都有这样的体会 - 就是计算出的电阻 Rsn 比实际实验得到的数值要小很多。大家有没有兴趣讨论一下 ~   

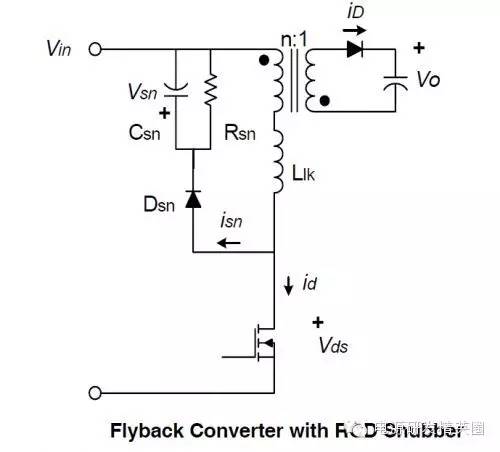
下面介绍一下本人在实验过程中发现的 3个原因 ~

1. 漏感测量的误差大 - 由于仪器和测试的问题导致漏感测量的误差可以很大（尤其是体积小变压器），通常是测得的漏感偏大。导致计算结果的不准确（电阻偏小）。

2. RCD计算公式中忽略了二极管Dsn的正向导通延迟时间和开关损耗，假设所有漏感引起的功耗都消耗在了电阻 Rsn 上，使得计算出的电阻数值偏小。

3. 计算公式忽略了漏感对 MOS管输出电容 Coss 的充电，而这一部分的能量是不能忽略不计的。

有关 RCD 的计算公式在网上可以找到不少，大致的算法都差不多。其中 Fairchild 的 AN-4147 比较具有代表性。对于RCD的计算公式，相信很多网友都很熟悉。在此不再重复。

请看：

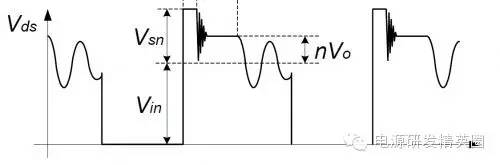
Vsn = 110V;　　Vor = 40V;　　Ipk = 4.2A;　　Llk = 2.79uH;　　fs = 50KHz;　　  根据公式

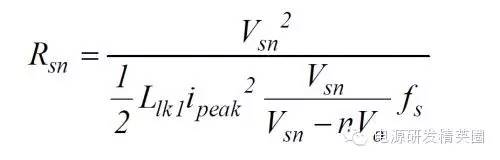
得出 Rsn = 6.2K  

实验得到的数值是 Rsn = 30K 时，可以做到 Vsn = 110V。与用公式计算的结果 6.2K 相差甚远 ~

上面只计算了电阻 Rsn 的数值，而没有算 Csn。是因为实际上电容的角色在这个线路中并不重要，本身也并不吸收（消耗）能量。只要数值取稍大一点就行了，对 Vsn 和 Rsn的大小也没有什么影响。有些网友在实验的时候，一会儿改电容 Csn，一会儿改电阻 Rsn，是对线路的理解不太够。

看到有网友不太清楚 Rsn 计算公式的推导，顺便在这儿推导一下 ~

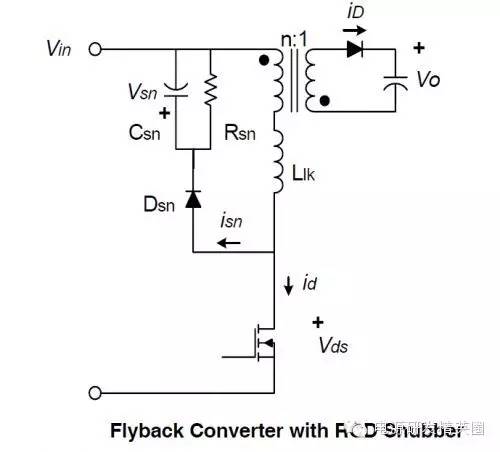
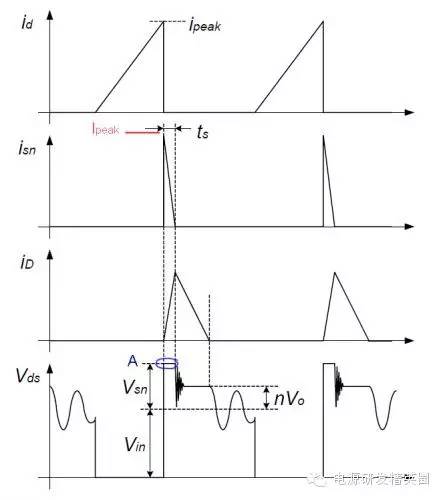
1. 当MOS管关断时，初级电流达到了最大值 Ipeak。电压Vds 迅速上升至A点，漏感 Llk上的能量开始对Csn冲电。2. Csn上的电压在整个过程中几乎不变，其大小是Vsn。3. 由于此时次级的整流管已经导通，次级圈上的电压被钳制到输出电压 Vo。反射电压 Vor (或者写成 nVo) 在初级建立。4. 漏感对 Csn 放电时，漏感上的电压被钳制到 Vsn - Vor。5. 漏感上的电流变化为

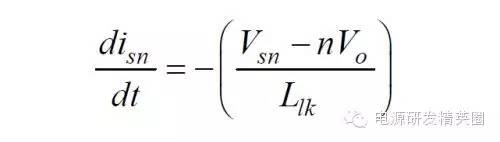
6. 在漏感对Csn充电的过程 ts 中，漏感两端的电压始终是 Vsn - Vor。7. 充电电流 isn 由初始值 Ipeak 一路线性下降到 0，此时漏感上的能量全部释放掉了。

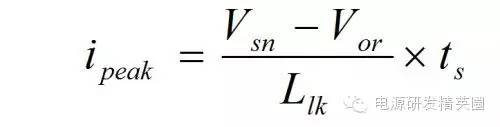
8. 由于电流 isn 的变化是线性的，可以用几何的方法计算出 Csn 在一个周期里充电的总能量是

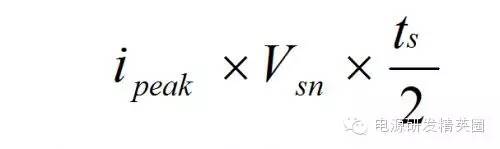
9. RCD 线路消耗的功率是

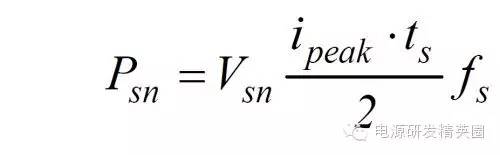
由

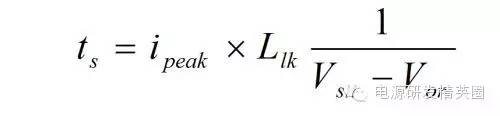
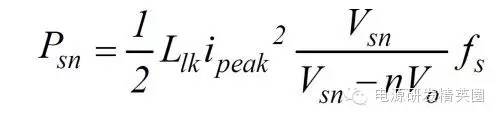
10. 假设 Csn 在放电的过程中，两端电压变化不大，其值为Vsn。则Rsn近似为

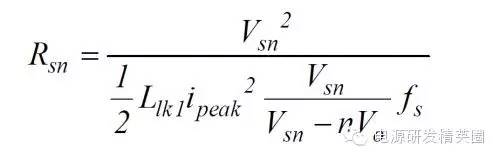
下面言归正传，讨论一下那些因素导致 RCD 计算的结果和实际的数值差别很大。

（一）漏感

我们在 上面 的例子中看到，计算的电阻值与实际得到的参数相差有几倍之多。如果相差百分之五十，那么在工程设计中还是有参考价值的。但是差出几倍的话，可以说计算的意义已经不大了。fairchild 的公式推导中，做了一些近似，而且把所有的元件都当成是理想元件。这其中不可避免的会引入一些误差。但本人在实验中发现这些还不是最主要的原因，影响最大的是漏感测量的误差造成的。

经常听到一些网友讲 - 测到的变压器漏感很大，尤其是小变压器。有的达到10%，还有人讲大到100% 的。甚至网上有人发帖说“漏感比感量还大” 。看标题就知道内容了。 我们知道初级线圈的漏感是 MOSFET 两端尖峰产生来源，漏感的大小直接影响到 RCD 吸收线路的参数。如果漏感多出几倍，那么Rsn的数值也肯定会差很远。 所以漏感的准确测量是非常重要的。有人（包括某些专家）说变压器的漏感通常在1-5%之间，所以可以估计个数值，用来计算 RCD。个人觉得这种说法不太靠谱  ~  如果实际的漏感是 5%，而你用 2% 去计算。结果不是要差出两倍吗

为什么小个子的变压器的漏感测出来会很大呢？ 其原因是变压器的每个绕组都有铜线内阻R存在。变压器越小，圈数越多，铜线上的电阻也就越大。 而测试电感的 RCL Meter在测试的时候并不知道有铜线内阻的存在，而是把线圈当做纯电感来测量。 我这里把变压器线圈简单的等效成一个电感与一个电阻的串联 （实际的等效威廉希尔官方网站 要复杂很多）

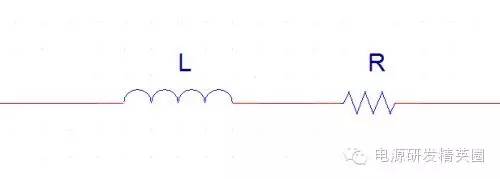
正常的情况下，圈数越多铜线内阻越大，电感量也越大。电感的感抗比内阻大的多，所以铜线的内阻对电感的测量影响不大。 但测漏感的时候情况就不一样了。这时候漏感只有线圈感量的 1 - 5%，而铜线内阻还是那么大。对于小变压器来说，铜线的电阻甚至比漏感的感抗还要大。测出的漏感的误差就可想而知了 ~

下面看一个实际的例子：

一个EE16的反激变压器， 初级绕了一、二百圈。感量3.0mH， 铜线内阻 3.3 Ω。 下面的表格显示了在不同频率下，初级绕组感抗 Zl 与铜线内阻的对比。可以看出当测试频率高于 1KHz 时，初级绕组的感抗都要比内阻大很多 。所以电感的测量误差很小。

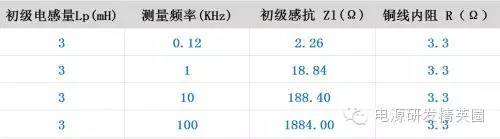
假设漏感是初级感量的 3%，也就是90uH，再看看漏感感量和铜线内阻的对照。不难发现当频率在10KHz的时候，感抗比铜线内阻也大不了几倍。这时候测量出的漏感还是有较大的误差。

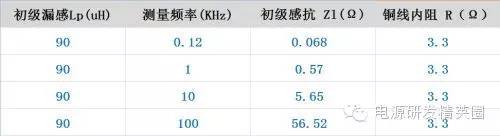
我们通常用的 RCL 测试仪， 有的测试频率能够达到 10KHz 或更高。也有的测试仪频率只有120Hz 和 1kHz 两种，我手上的巧好是后者。用 1KHz测量这个EE16变压器的漏感是 267uH，也就是差不多 9% 的初级感量。问过变压器的供应商，被告知如果用10KHz的频率测量，漏感大概是5-6% 的样子。各位的经验差不多是这样吧 ~

如果用120Hz的频率来测，漏感能有多少呢？ 实测的漏感有 80%还多。测出的漏感比感量还大，应该是用120Hz的频率测的 ~

由上面的表格中，我们可以看出 RCL 仪器测试频率和漏感的测量误差之间存在的关系。在测量漏感的时候，（在低频范围内）频率越高相对的误差会越小。但即使用10KHz的频率，也还是有较大的误差。然而，很多时候我们手上的仪器有限，不一定能提供更高的频率。那只有考虑其他的办法了 ~

下面介绍一下我在实验中采用的漏感测试方法 - LC 谐振的方法。

LC 谐振的威廉希尔官方网站 大家都很熟悉，一个电感和一个电容，串联或是并联的线路。在某一频率会产生谐振，此时的振幅最大。利用这个线路，在已知电容容值的情况下，找到谐振的频率。进而可以计算出电感的数值。

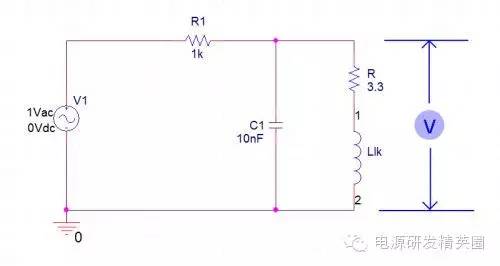
如上图，左边用信号源提供正弦波信号，在电感的两端（包括了串联的铜线内阻）用示波器观察信号的幅度。并记录下幅度最高时的输入频率 f 。

上面例子中的 EE16反激变压器，测得的初级漏感的谐振频率是 f = 169KHz。线路中的电容值实际测得是 C= 9.83nF 。 这个LC谐振威廉希尔官方网站 的谐振频率表达式如下：

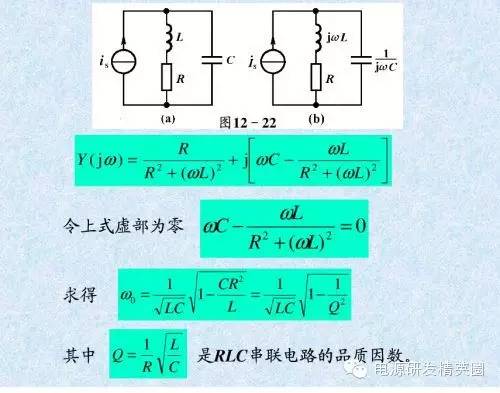
由于 CR2/L 部分很小，可以忽略不计。频率的公式可以简化为：

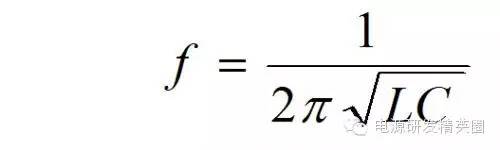
计算出变压器的初级漏感 Llk = 90uH， 相当于 3% 的初级电感。 这个数值比用 RCL 测试仪在 1KHz 频率时测得的 9% 的漏感要小 3 倍，也比用 10KHz 频率测得的 5-6% 的漏感要小很多 ~

由此可见 - 漏感测量的误差可以很大，由此而计算出的 RCD 参数其准确性也会大打折扣。

对上面测试的 LC 谐振的频率，我用线路模拟验证了一下。结果吻合的很好 ~

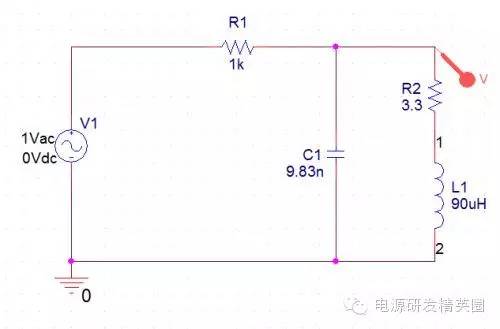
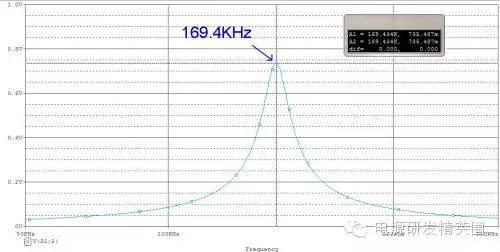
如果减小了漏感的误差，那么RCD计算的数值是否与实验参数接近了呢？，我们下面做个实验来验证一下 ~

一个反激电源工作在DCM模式；　　变压器 PQ3230：初级电感 Lp = 205uH；　　初级漏感 Llk = 5.5uH （@ 1KHz）;  用LC谐振的方法测得： Llk = 2.1uH开关频率 fs = 76KHz初级电流 Ipeak = 3.13A   （输出 12.4V / 5A)钳位电压 Vsn = 210V反射电压 Vor = 85V ； Vin = 140V根据 fairchild 的公式

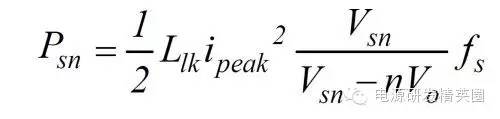
得到由漏感而引起的功率损耗是 Psn = 1.32W； 理论上这些能量都消耗在 Rsn上，由公式

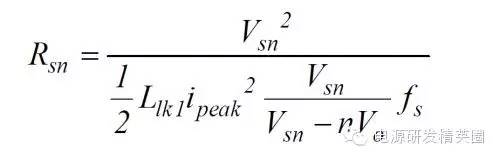
计算出 Rsn= 33K

实验得到的RCD参数是： Dsn = UF4007；　　Csn = 0.01uF/1KV；　　Rsn = 39K / 3W

与计算出的电阻 Rsn 的 33K 相差的不多。 如果计算出的数值能如此地接近实验的结果，那么已经是很不错了。

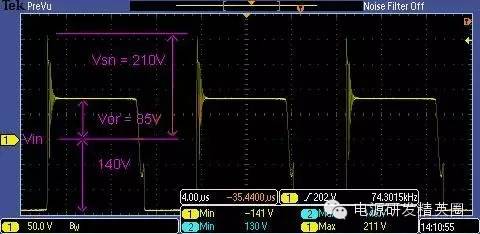
但是仔细观察一下各处的波形，发现事情还没有那么简单 ~

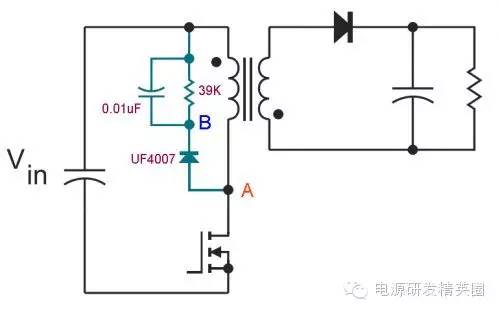
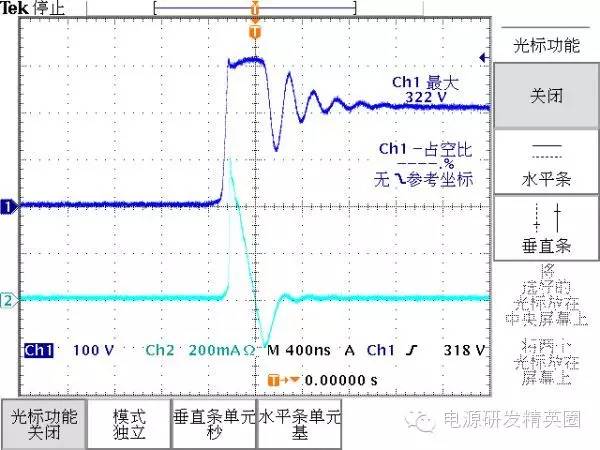
下图中黄色为A点波形；蓝色为B点波形

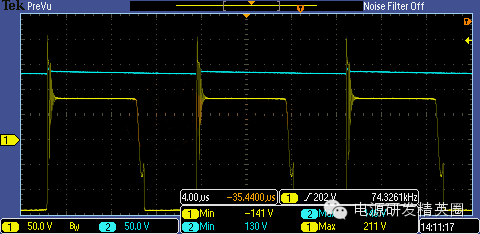
放大一点看 ~

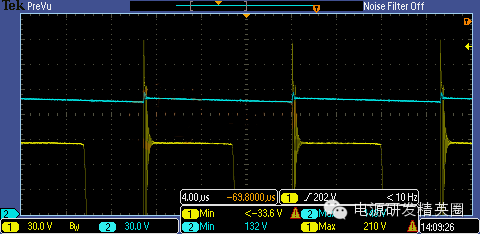
再放大一点 ~

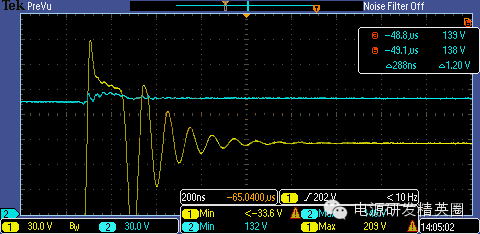
我的RCD的波形怎么是这样的？

Ａ点的波形和Ｄ中的电流，然后是

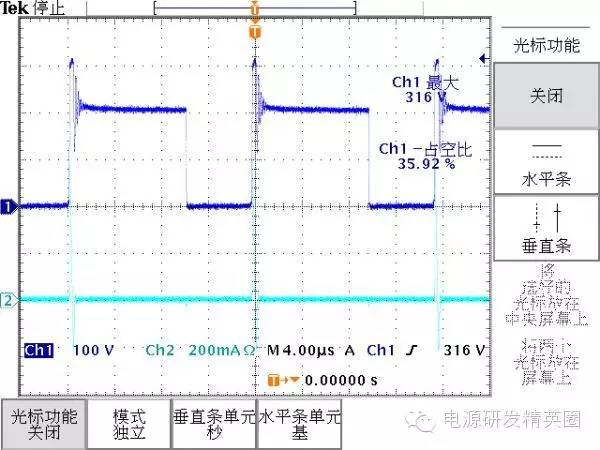
展开：

上贴提到二极管 UF4007 有功率消耗。但具体功耗是多少，很难准确的计算或测量。 只能根据其发热的情况，大致地估计一下。为了方便测量，把二极管 UF4007 和 Rsn 39K 搬到板子的背面。

然后用红外测温仪记录一下电阻和二极管上的温度

凭元件上的温度来估计功耗肯定是不会很准的，但也没有想出什么更好的办法。 3W 电阻上的功率损耗是0.5W、温度74.3C， 而个子小一半的二极管上的温度是66.1C。估计UF4007上的功耗大致有0.2~0.25W吧 ~

由实验看出 - 由于RCD 吸收线路中的二极管不是理想元件，本身有一定的损耗。这是RCD 公式计算误差大的另一个原因（导致计算出的电阻阻值偏小） ~

（三）Coss

大家都知道 MOS 管的输出电容 Coss 的存在。Coss上面会储存和释放能量，MOS管的开关过程中，也会造成功率损耗从而影响效率。

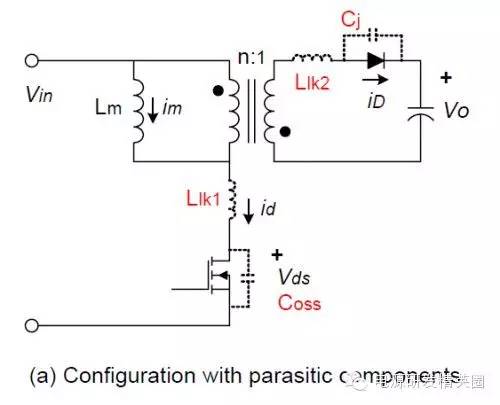
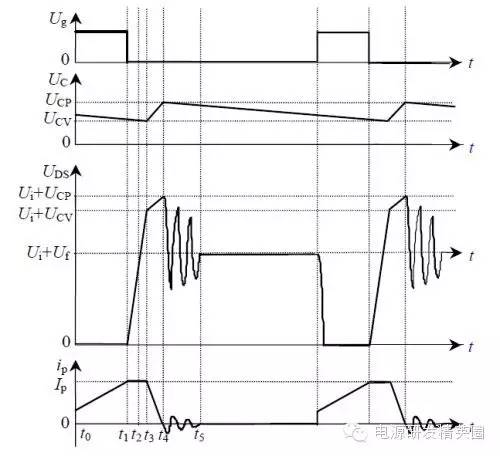
当MOS管关闭后, Vds 两端的电压迅速上升。电容 Coss 同时被充电。在一技术文文章中，（西安科技大学）刘树林教授的观点是 - “流过变压器原边的电流IP首先给漏源寄生电容Cds（Coss）恒流充电(因LP很大)，UDS快速上升(寄生电容Cds较小)，变压器原边电感储存能量的很小一部份转移到Cds（Coss）”

而某网站官方  认为“漏感能量在传递到RCD钳位威廉希尔官方网站 之前，是有损耗的，损耗在于MOS管的输出电容上，也就是Coss，因为，漏感能量要先给它充能，使得它两端的电压能达到钳位威廉希尔官方网站 的钳位电压，达到了钳位电压后，二极管才会导通，接着才是漏感能量向钳位威廉希尔官方网站 传递能量”

我比较认同后者。起码来说漏感从一开就参与了给Coss充电，而当电压上升到Vin+Vor的时候，漏感继续给Coss充电，直至Coss上的电压升至Vin+Vsn。 一个周期内漏感充电给Coss 的能量是

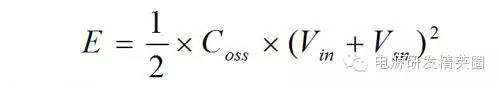
这些能量在Coss与漏感Llk的谐振中衰减，部分传递到次级输出。剩余的部分在MOS再次开通时消耗在MOS管的导通电阻上了。其功率损耗为

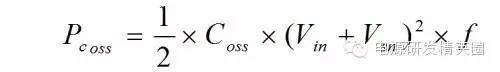
要想计算出Coss上的能耗，首先要知道 Coss 是多少。本例中所用的是‘富士’的 FMV11N60E。规格书中的 Coss 150pF（typical）是在电压25V时的数据. Coss 随电压变化的曲线如下 -

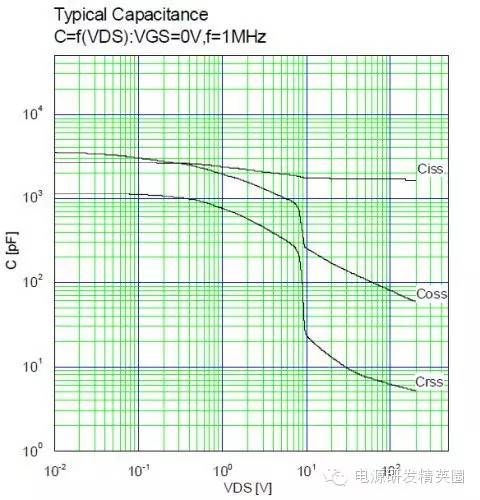
由图中可以看出当电压升至几百V 的时候， Coss 就只有几十 pF 了。 于是某网站指出 - “MOS管输出电容上损耗的能量是非常小的，大概在漏感能量的 3%左右，所以可以忽略不计”

Coss上的能耗是不是真的很小，以至于可以忽略不计呢？ 我们还是需要具体的计算一下。显然这个 Coss 是很难准确计算出来的，只有用实验的手段来测量其实际的数值。

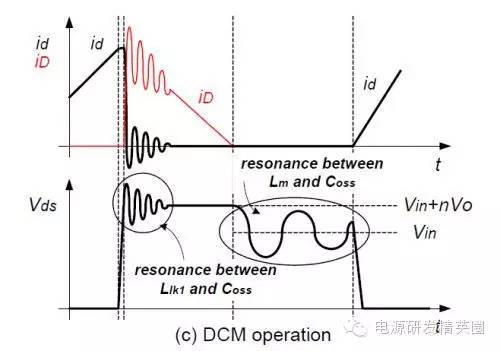
上面这个波形是典型的反激 DCM mode的开关管Vds的样子。图中左边的谐振是初级漏感 Llk和 Coss组成的，右边的谐振是初级电感 Lp和 Coss构成的。

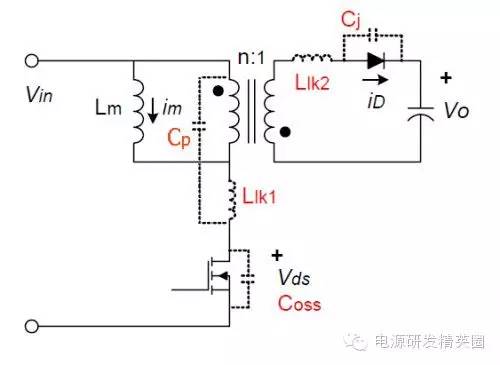
实际上参与谐振的除了 Coss 以外，还有其他的一些电容存在 - 包括变压器的初级线圈线间/层间电容 Cp（见上图）、线路的分布电容以及次级反射到初级的电容等等 ..... 我们在这里用 Ctot 来代表所有这些电容的总和。 所以实际上，上图中的谐振分别是 Llk和 Ctot、以 Lp 和 Ctot 所构成的。这里我们忽略其他的电容成分（以便于计算），近似地认为 Ctot = Coss + Cp。

这两个谐振的频率是很容易在波形上测量出来的。而初级电感 Lp和漏感 Llk 都是已知的，所以计算出 Ctot 并不困难 ~

1. 先看看初级电感 Lp和 Ctot 的谐振

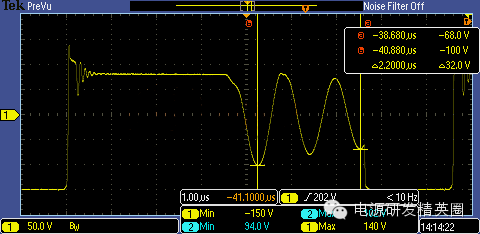
由图中读出谐振的振荡周期是  2.2uS / 2 = 1.1uS；已知Lp = 205uH，由谐振公式

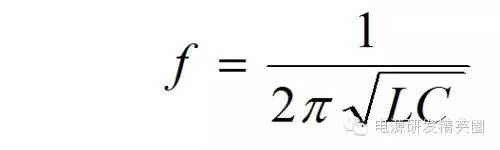
计算出 Ctot 1 = 149 pF

2. 再看看初级漏感 Llk和 Ctot 的谐振

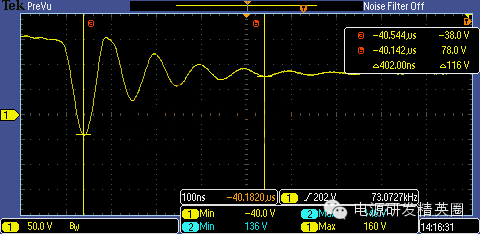
由图中读出谐振的振荡周期是  402nS / 4 = 100.5nS；已知漏感 Llk = 2.1uH，由谐振公式

计算出 Ctot 2 = 122 pF

由这两个谐振算出来的 Ctot 差别有点儿大，原因待查（也可能是测量的误差）。由于其中的 Coss本身不是定数，随电压升高而下降，所以这个趋势还是对的 ~   我们以Ctot  = 122 pF 继续下面计算

上面计算中 Ctot = 122pF ，接下来算一算Coss 到底是多少 ~

由于 Ctot = Cp + Coss， 所以还要知道 Cp的大小才行。用12贴中谐振的方法，测得初级线圈电感和电容的谐振频率为1.75MHz 。根据谐振频率公式

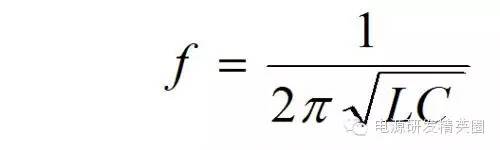
计算出 Cp = 43pF  于是有  Coss = 122 - 43 = 79pF。 这个电容值实际上还包括一些线路分布电容、次级反射电容等等.......所以实际的 Coss 会比这个值还小。

计算 Coss上的能耗 -

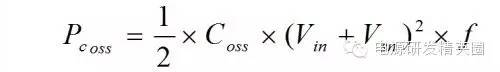
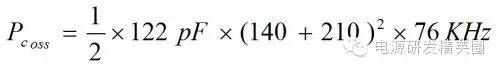
得到 Pcoss = 0.368W  这个结果显然不止 3% 那么小  ~ 至此，让我们回过头来看看各部分的能耗。看看原本假设全部消耗在RCD 电阻上的能量实际上去了哪里 -

电阻 Rsn 上的能耗 　　　　　　　　PRsn = 0.5W二极管 UF4007上的能耗　　　　　　PDsn = 0.2~0.25WMOS管输出电容 Coss上的能耗 　　　PCoss = 0.368W -------------------------------------------------------------------上面各项的总和是   　　　　　　　　1.07 ~1.12W

这个结果与用公式计算出来的 RCD 线路的功耗 1.32W 已经比较接近 。由于在计算和测试过程中有很多的近似甚至估计，误差可以有10-30%。不过即使这样，也还算是吻合的不错 ~