

基于FKM规范对非焊接构件采用名义应力法及局部应力法进行疲劳强度评估的流程
电子说
描述
导读:FKM(《Analytical Strength Assessment of Components in Mechanical Engineering》)规范是德国机械工程研究委员会根据机械产品在实际工程中的应用情况,统计出的针对由钢、铸铁及铝材料制成构件的静强度及疲劳强度的评估规则,考虑了大多数对构件强度(静态和动态)产生影响的因素(表面状况、残余应力、结构细节等),可以基于名义应力法或局部应力法使用利用率对焊接和非焊接构件的静强度及疲劳强度问题进行评估,在欧洲各领域得到了大范围的应用。
本文分为上、下两篇,上篇主要结合规范,简要介绍基于FKM规范对非焊接构件采用名义应力法及局部应力法进行疲劳强度评估的流程,希望大家能够对采用FKM规范进行疲劳强度评估的过程有概念上的了解。
下篇将结合FKM针对非焊接构件的手动计算实例及软件计算实例进行介绍,从实例化的的角度分别介绍FKM在非焊接构件疲劳强度评估中的手动及软件计算过程,同时验证FKM Inside ANSYS软件计算结果的准确性及方便性。
以下是正文
基于FKM规范进行疲劳强度评估采用以下8个步骤进行,如下图1所示,通过应用有限元分析方法、工程计算方法和实验检测得到评估部位的最大交变应力幅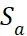 (或
(或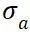 ),根据材料特性和结构设计参数得到构件疲劳强度极限
),根据材料特性和结构设计参数得到构件疲劳强度极限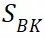 (或
(或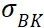 ),然后根据安全因子
),然后根据安全因子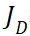 计算得到部件的强度利用率
计算得到部件的强度利用率
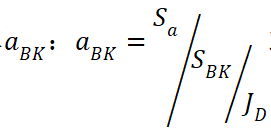
或
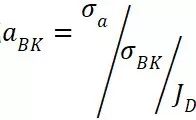
若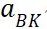 小于1,则构件在这样的循环载荷作用下被评估部位满足疲劳强度要求,否则不满足疲劳强度要求。
小于1,则构件在这样的循环载荷作用下被评估部位满足疲劳强度要求,否则不满足疲劳强度要求。
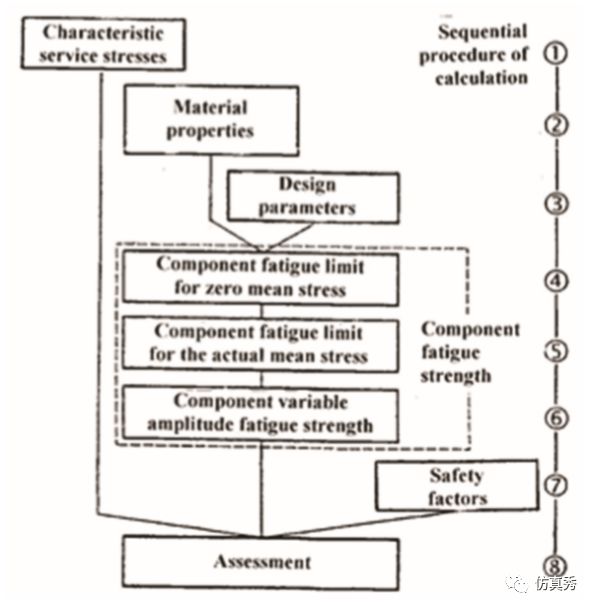
图1 疲劳强度评估过程
下面针对各步骤展开进行说明:
一、特征工作应力:
1、相关说明:
a. FKM规范的疲劳方法适用于高周疲劳(总循环次数 )
)
b. 对于变幅应力谱的参数:
① 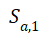 最高幅值,i=1(谱中的最大值);
最高幅值,i=1(谱中的最大值);
②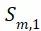 对应的平均应力
对应的平均应力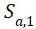 ,step1;
,step1;
③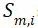 第i步的平均应力
第i步的平均应力
④  对应所需疲劳寿命的总循环次数(需要的总循环次数),
对应所需疲劳寿命的总循环次数(需要的总循环次数),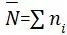 (i从1到j)
(i从1到j)
⑤ 每一段的循环次数,其中i=1,……j
每一段的循环次数,其中i=1,……j
⑥ i:谱中的步数,i=1,……j
⑦ j:谱中的最后一步
⑧ V:潜在损伤,谱形状的特征值
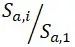 以及
以及 描述了应力谱的形状,
描述了应力谱的形状,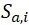 总是正值,
总是正值, 可以是正值、负值或者0。
可以是正值、负值或者0。
c.对于横幅载荷循环:横幅载荷循环可以看作变幅载荷循环的特例,i=1
① 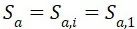
②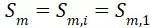 以及
以及
③ 
④ 应力比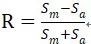
d.横幅S-N曲线的特征值:在材料S-N曲线的基础上考虑了设计因子及平均应力因子的影响
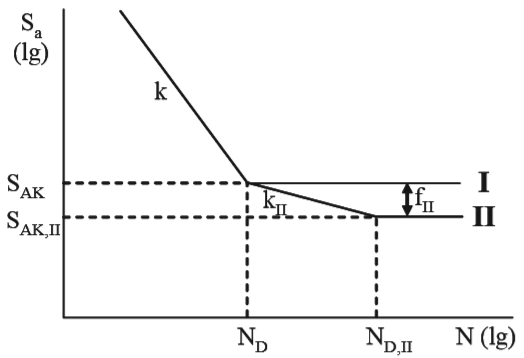
图2 横幅S-N曲线
① 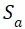 :应力幅
:应力幅
② 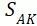 :构件的名义疲劳极限
:构件的名义疲劳极限
③ 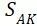
④ N :循环次数
⑤ 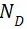 :构件横幅S-N曲线拐点处的循环次数
:构件横幅S-N曲线拐点处的循环次数
⑥ 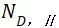 :只用于构件model Ⅱ横幅S-N曲线;第二段拐点处的循环次数
:只用于构件model Ⅱ横幅S-N曲线;第二段拐点处的循环次数
⑦ K:对于S-N曲线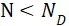 段的斜率
段的斜率
⑧  :只用于构件model Ⅱ横幅S-N曲线;对于S-N曲线
:只用于构件model Ⅱ横幅S-N曲线;对于S-N曲线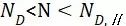 段的斜率
段的斜率
⑨ 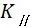
2、名义应力:针对杆状及壳状结构:
① 轴向应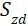
② 弯曲应力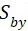 以及
以及 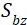
③ 剪切应力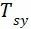 以及
以及 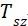
④ 扭转应力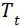 (壳状结构忽略)。
(壳状结构忽略)。
与各应力分量相对应的幅值及平均应力分别为:
⑤ 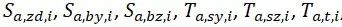
⑥ 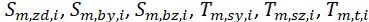
采用名义应力法需要材料具有足够的韧性(本规范中材料的韧性基于延展率A进行考虑,一般规定A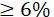 ),例如GJS,GJM以及铝材(锻铝或铸铝)等材料。
),例如GJS,GJM以及铝材(锻铝或铸铝)等材料。
通常,作用于杆状构件的应力类型包括:一个轴向应力(拉伸或者压缩),两个弯曲应力,两个剪应力以及一个扭转应力,各应力分量计算公式参考如下:
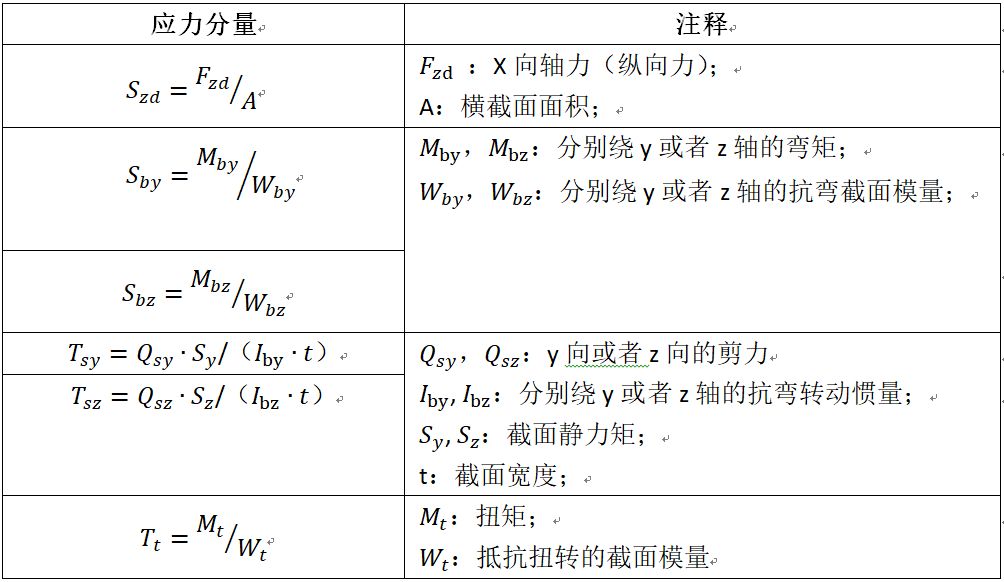
3、局部应力:局部应力包含了由几何缺口产生的峰值应力。在可以定义参考截面的情况下,可以通过采用名义应力乘以应力集中因子的方法计算局部应力。然而,局部应力法通常采用能反映构件真实几何形状的实体模型利用有限元方法计算得到。局部应力法适用于所有构件。局部应力说明如下,参见FKM规范Figure0.3-3:
① 2D:应力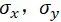 以及
以及 在平面内;Z方向的正应力及剪应力被忽略,或者
在平面内;Z方向的正应力及剪应力被忽略,或者
②3D:注意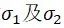 的定义与常规不同,在FKM规范中将构件表面的主应力定为
的定义与常规不同,在FKM规范中将构件表面的主应力定为
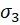 是垂直于表面的应力。主应力
是垂直于表面的应力。主应力

图3 参考点处应力分量
二、材料属性的修正
针对疲劳评估的材料属性部分,基于静强度已经修正完成的抗拉强度极限,同时需要考虑疲劳强度因子、温度因子。
1、疲劳强度因子:
针对完全相反轴向应力以及剪切应力的材料的疲劳极限计算公式:
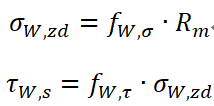
注意:此处公式中的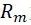 为静强度评估中已经考虑了几何尺寸因子及各向异性因子的抗拉强度极限。
为静强度评估中已经考虑了几何尺寸因子及各向异性因子的抗拉强度极限。
 :完全相反应力的抗拉疲劳强度因子;
:完全相反应力的抗拉疲劳强度因子;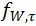 :完全相反应力的剪切疲劳强度因子(相关值参见见FKM规范Table2.2.1或Table4.2.1)。
:完全相反应力的剪切疲劳强度因子(相关值参见见FKM规范Table2.2.1或Table4.2.1)。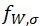

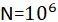 的循环次数有效。
的循环次数有效。
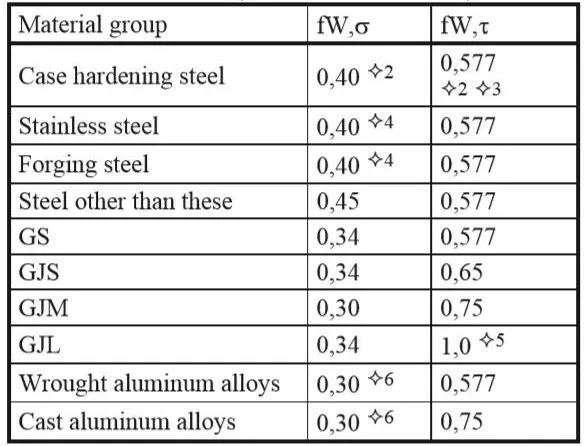
2、温度因子
FKM规范将材料的工作环境温度分为常温、低温和高温,低温情况在FKM规范中未考虑。常温条件下,可忽略温度对材料强度的影响。因此温度因子主要考虑了材料强度由于温度升高所引起的强度降低。针对疲劳强度的温度因子采用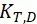 表示。
表示。
① 针对细晶粒结构钢,当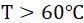 时:
时:

② 针对其他类型钢,当 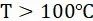 时:
时:

对于不锈钢,无对应的值。
③ 针对GS, 

④ 针对GJS,GJM以及GJL, 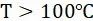
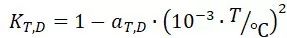
其中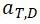 为常数。参见FKM规范Table2.2.2
为常数。参见FKM规范Table2.2.2
⑤ 针对铝材料,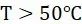 时:
时:
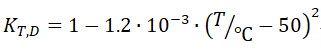
3、设计参数的修正
针对非焊接构件疲劳评估设计参数的修正,需要考虑疲劳缺口因子、粗糙度因子、表面处理因子、覆盖层因子以及GJL因子。综合考虑了对疲劳强度有影响的相关因素后,采用下列公式分别计算拉压、弯曲、剪切及扭转应力的设计参数 :
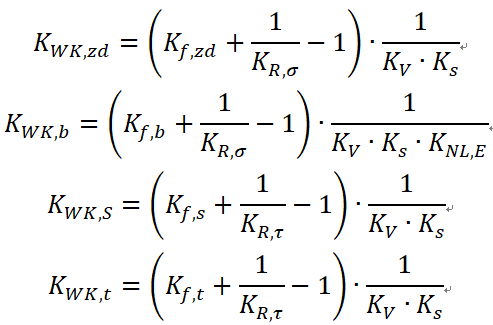
其中: ,疲劳缺口因子;
,疲劳缺口因子;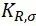 ,粗糙度因子;
,粗糙度因子;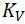 ,表面处理因子;
,表面处理因子; 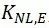 ,灰口铸铁因子。其中疲劳缺口因子的计算最为复杂,各相关因子的计算参见下面详细的说明:
,灰口铸铁因子。其中疲劳缺口因子的计算最为复杂,各相关因子的计算参见下面详细的说明:
① 疲劳缺口因子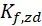




② 粗糙度因子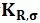 (或者
(或者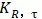 )的计算
)的计算
粗糙度因子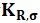
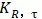

③ 表面处理因子 的计算
的计算
表面处理因子

④ 覆盖层因子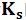 的计算
的计算
覆盖层因子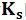

⑤ 灰口铸铁因子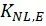 的计算
的计算
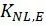

4、构件疲劳强度的计算
构件的强度极限采用如下过程计算:-
首先,考虑了设计因子的对称循环应力下的构件的疲劳极限;
其次,确定与平均应力因子相关的构件疲劳极限的幅值;
最后,确定与变幅疲劳强度因子相关的构件变幅疲劳强度的幅值。
① 对称循环应力的构件疲劳极限的计算

② 考虑了平均应力的构件疲劳极限的计算




③ 构件变幅疲劳强度的计算
针对名义应力法及局部应力法构件变幅疲劳强度的计算方法相同,注意区分S及 的表达方式即可。
的表达方式即可。
a.对于常幅应力谱采用疲劳极限评估(或者耐久极限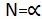 评估)
评估)
b.对于变幅应力谱采用变幅疲劳强度极进行评估。变幅疲劳极限评估的简化方法是基于等效损伤应力幅,在这种情况下,采用疲劳极限评估的形式。



备注:关于变幅疲劳强度的极限值  或
或 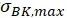 的计算请参见规范,本文不进行说明。
的计算请参见规范,本文不进行说明。
5、安全因子的计算
名义应力法及局部应力法中总的安全因子的计算公式相同,公式如下:
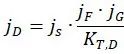
其中:
 是载荷因子,
是载荷因子,
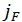 是材料安全因子,该因子针对钢及锻铝合金,考虑了失效后果及是否进行定期检查的影响,具体数值参见FKM规范Tables.4.5.1以及4.5.3
是材料安全因子,该因子针对钢及锻铝合金,考虑了失效后果及是否进行定期检查的影响,具体数值参见FKM规范Tables.4.5.1以及4.5.3
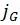 是铸造因子,该因子只针对铸铁及铸铝材料进行考虑,具体数值参见FKM规范Table.4.5.2
是铸造因子,该因子只针对铸铁及铸铝材料进行考虑,具体数值参见FKM规范Table.4.5.2
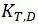 是温度因子
是温度因子
6、疲劳强度评估
基于构件的实际循环应力幅、修正后的构件疲劳强度极限以及安全因子计算构件的疲劳利用度。可以计算如下情况:
① 变幅疲劳强度;② 有限寿命的疲劳强度③ 疲劳极限或者④  的耐久极限
的耐久极限
相关公式参见如下表格:

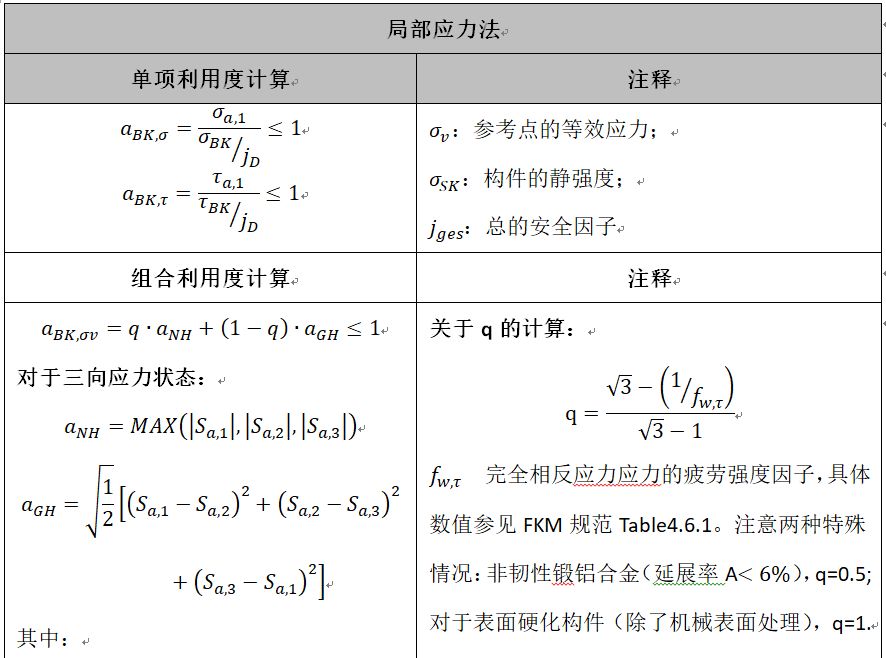

7、其他说明:
① FKM规范系统性很强,基于名义应力法及局部应力法的疲劳强度评估流程清晰,相关过程均可以通过规范内的公式及表格得到相对准确的数据。本文鉴于篇幅原因,不能将所有过程公式及表格一一列出,请感兴趣人员系统学习FKM规范。
② 本文只是针对主体内容进行简单整理,其中部分内容未特殊性说明,还请感兴趣者详细学习FKM规范。
③ FKM Inside ANSYS是结合FKM规范在ANSYS Workbench平台中开发的强度评估软件,下一期将针对FKM规范及FKM Inside ANSYS软件进行非焊接构件疲劳强度实例评估介绍,欢迎关注。
④ 鉴于作者水平有限,不当之处还请谅解并欢迎指出,共同探讨。
-
快速高性能应力检测技术_戬威2017-08-24 0
-
普通焊接结构存在的问题2018-09-04 0
-
利用有限元方法对280M1-2型三相异步电机的法兰结构强度进行分析校核2023-03-02 0
-
提高焊接接头疲劳强度的超声波冲击法2010-01-26 623
-
焊缝匹配影响焊接残余应力的研究2010-01-26 546
-
弹塑性应力及电测法的综合实验2010-11-23 599
-
焊接应力的不利影响_消除焊接应力的有效方法2020-02-04 3481
-
焊接应力产生的原因_减少焊接应力的措施2020-02-04 12429
-
焊接残余应力的特点_焊接残余应力的分类2020-02-04 8247
-
焊接残余应力影响有哪些_焊接残余应力的控制措施2020-02-04 5099
-
焊接结构疲劳强度相关知识2021-11-12 1770
-
金属材料疲劳强度的八大主要影响因素2022-04-21 1243
-
关于结构应力集中问题 引起构件破坏的主要因素2022-08-11 3207
-
焊接结构疲劳分析:结构应力法与数据物理驱动模型浅谈2022-12-08 2759
-
焊接应力是什么?6种方法轻松去除2024-11-28 214
全部0条评论

快来发表一下你的评论吧 !

