Apollo代码学习—MPC与LQR比较

LQR （线性二次调解器）理论是现代控制理论中发展最早也最为成熟的一种状态空间设计法。特别可贵的是，LQR可得到状态线性反馈的最优控制规律，易于构成闭环最优控制。

LQR 最优设计是指设计出的状态反馈控制器 K 要使二次型目标函数 J 取最小值，而 K 由权矩阵 Q 与 R 唯一决定，故此 Q、R 的选择尤为重要。

MPC（模型预测控制）是一种先进的过程控制方法，在满足一定约束条件的前提下，被用来实现过程控制，它的实现依赖于过程的动态模型（通常为线性模型）。

在控制时域（一段有限时间）内，它主要针对当前时刻进行优化，但也考虑未来时刻，求取当前时刻的最优控制解，然后反复优化，从而实现整个时域的优化求解。

本文由社区开发者——吕伊鹏撰写，对MPC与LQR进行了较为详细的比较，希望这篇文给感兴趣的同学带来更多帮助。

Apollo中用到了PID、MPC和LQR三种控制器，其中，MPC和LQR控制器在状态方程的形式、状态变量的形式、目标函数的形式等有诸多相似之处，因此结合自己目前了解到的信息，将两者进行一定的比较。

MPC(Model Predictive Control，模型预测控制)和LQR(Linear–Quadratic Regulator，线性二次调解器) 在状态方程、控制实现等方面，有很多相似之处，但也有很多不同之处，如工作时域、最优解等，基于各自的理论基础，从研究对象、状态方程、目标函数、求解方法等方面，对MPC和LQR做简要对比分析。

本文主要参考内容：

【1】龚建伟,姜岩,徐威.无人驾驶车辆模型预测控制[M].北京理工大学出版社, 2014.

【2】Model predictive control-Wikipedia.

【3】Linear–quadratic regulator-Wikipedia.

【4】Inverted Pendulum: State-Space Methods for Controller Design.

【5】王金城. 现代控制理论[M]. 化学工业出版社, 2007。

LQR的研究对象是现代控制理论中以状态空间方程形式给出的线性系统。MPC的研究对象可以是线性系统，也可以是非线性系统，只不过为了某些需求，如时效性，计算的便捷，操控性等，一般会将非线性系统转换为线性系统进行计算。非线性系统的线性化可参考上一篇文章。

Apollo中，LQR和MPC控制器都选用的单车动力学模型作为研究对象，单车动力学模型为非线性系统，但LQR和MPC控制器的目的是为了求最优控制解，在具体的优化求解时，均通过线性化方法将状态方程转化为线性方程进行求解，所以，可以说Apollo中LQR和MPC控制器的研究对象均为线性系统。

LQR的状态方程多以微分方程的形式给出，如：

是一个连续线性系统，在计算过程中需要转换为如公式3的离散线性系统。

MPC的状态方程可以为线性系统，可以为非线性系统，非线性系统形如下：

线性系统如公式3所示：

但LQR和MPC在计算求解时基本都是基于离散线性方程计算的。公式1可以很方便的转化为公式3的形式。

按照维基百科的说法：

LQR在一个固定的时域上求解，且一个时域内只有一个最优解，而MPC在一个逐渐消减的时域内(in a receding time window)求解最优解，且最优解经常更新。

可以结合MPC的滚动优化，以及图1进行理解：

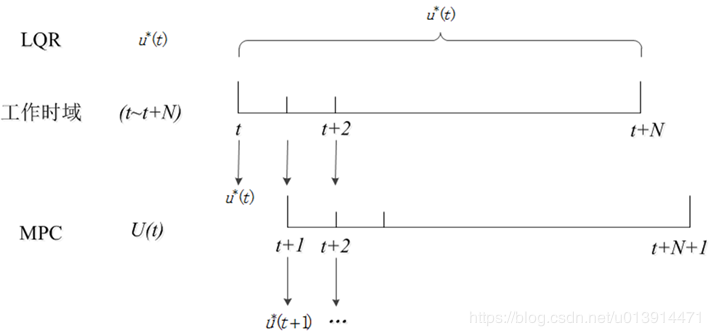
图1 MPC和LQR的工作时域

针对同一工作时域[t,t+N]，LQR在该时域中，有唯一最优控制解u∗(t) ，而MPC仅在t时刻有最优解u∗(t)，但它会计算出一个控制序列U(t) ，并仅将序列的第一个值u∗(t)作为控制量输出给控制系统，然后在下一采样时间结合车辆当前状况求取下一个最优控制解u∗(t+1)，这就是MPC所谓的滚动优化。

这么做的目的是为了使控制效果在一定时间内可期，并且能根据控制效果尽早调整控制变量，使实际状态更切合期望状态。

此外，LQR的工作时域可以拓展到无限大，即可以求取无限时域的最优控制解。而MPC只针对有限时域。

优化求解问题一般离不开目标函数的设计。

LQR的目标函数的一般形式为：

其中，终端状态，

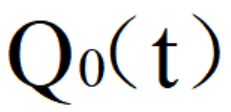
正定的终端加权矩阵，x为状态变量，多为各种误差，u为控制变量，Q为半正定的状态加权矩阵，R为正定的控制加权矩阵，实际应用中，Q、R多为对角矩阵。

MPC的目标函数的一般形式为：

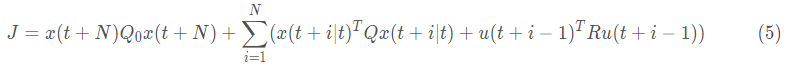
其中，

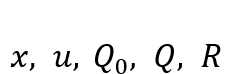
从形式上可以看出，LQR的目标函数为积分形式，MPC的目标函数为求和形式，但其实都是对代价的累计。

两者第一部分均为终端代价函数，当系统对终端状态要求极严的情况下才添加，一般情况下可省略。

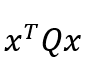跟踪代价，表示跟踪过程中误差的大小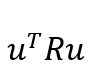，控制代价，表示对控制的约束或要求等。

正如工作时域所述，针对同一工作时域，LQR有唯一最优控制解，也就是在该控制周期内，LQR只进行一次计算。

而MPC滚动优化的思想，使其给出该时域内的一组控制序列对应不同的采样时刻（采样周期和控制周期不一定相同），但是只将该序列的第一个值输出给被控系统，作为该时刻的最优控制解。

因此，对于工作时域[t,t+N]，LQR只有唯一解，对于线性MPC，本质是凸优化问题，只有唯一解；但非线性MPC，可能会有N个local optimal。

最优控制解的求取多基于目标函数进行，取线性约束下的目标函数的极值为最优控制解。对于系统为线性，目标函数为状态变量和控制变量的二次型函数的线性二次性问题，最优解具有统一的解析表达式。

Apollo中的MPC将优化问题转化为二次规划问题，利用二次规划求解器进行求解。横向控制中用的是LQR调节器，它通过假设控制量u(t)不受约束，利用变分法求解。

此外，LQR对整个时域进行优化求解，且求解过程中假设控制量不受约束，但是实际情况下，控制量是有约束的。

而MPC通常在比整个时域更小的时间窗口中解决优化问题，因此可能获得次优解，且对线性不作任何假设，它能够处理硬约束以及非线性系统偏离其线性化工作点的迁移，这两者都是MPC的缺点。