

离散傅里叶变换DFT中的第5个问题:频域抽样进行总结
描述
继续上一篇,本文对离散信号的频域分析(共5节)中的第3节——离散傅里叶变换DFT(Discrete- Fourier Transform)中的第5个问题:频域抽样进行总结。

3.5 频域抽样
实际上,DFT,就是频域抽样。包括三个问题,这三个问题环环相扣、层层推进。
1、DFT与DTFT、z变换的关系
先从公式上看三个变换的关系,再结合z平面的单位圆的概念,从图形上理解。如下图:

图1

图2
毫无疑问,DFT的自变量k为离散的,而DTFT的自变量w、以及z变换的自变量z都是连续变量。DFT是两外两种变换的离散采样值。因为这种采样是在频域,所以称为”频域采样“。
那么问题来啦:

不管在那个域进行抽样,其数学本质都是用一些离散的数值代替原来连续变化的函数,或者说用一些离散的点代表原来连续的曲线。能不能代表?取决于两个因素:一是这些离散的点的间隔,即抽样间隔;二是原来那条连续曲线的变化起伏程度。这就是第二个问题:频域抽样定理。
2、频域抽样定理
傅里叶分析方法的好处在于,建立起时域和频域的一种重要的对应关系:一个域离散抽样,另外一个域周期延拓。所以,研究时域抽样时,把问题对应到频域上去研究;那么现在研究频域抽样时,又要把问题对应到时域上去研究。毫无疑问,时域上会周期延拓。如下图:

图3
既然是以N为周期延拓,条件自然而然就出来了:

图4
也就是说,只要满足频域抽样定理的条件,频谱离散的抽样值X(k)可以完全表征连续频谱X(e^jw)或者X(z)。
问题又来了,怎么表示?这就是第三个问题:频域的插值恢复。
3、频域的插值恢复
与时域抽样的恢复完全相同的思路,用离散的样本值乘以一个插值函数,得到一个连续的函数,只不过这里的插值函数是关于w或z的函数。下面的任务就是找这个函数fai(w)或fai(z)。

图5
z变换的形式更为简洁,因此首先解决由X(k)得到X(z)的问题。
以下推导过程的大致思路:把z变换定义式中的x(n)用IDFT的公式替换,然后交换求和次序,再利用旋转因子的性质,即可得到。如下图:

图6
解决了由X(k)得到X(z)的问题,将z换成e^jw,自然就得到了X(e^jw)。如下图:

图7
把内插公式和内插函数总结如图8,这个内插函数的幅度部分的图形我们可以画出来,我们发现,它在一些固定的位置(2Π/N的整数倍处)是零,而2Π/N恰好是频域抽样时的间隔,这是巧合吗?显然不是,这是必然的。

图8
我们把内插公式展开来看,如图9所示。也就是说,把各个频域抽样值X(k)与做相应平移后的内插函数(平移2Π/N的k倍)相乘,再相加,就得到连续的频谱函数X(e^jw)。与第k个抽样值相乘的内插函数,在所有其他抽样点处刚好是零点,只有在第k个抽样点处的值不为零(值为1)。所以,重建后的这个连续函数,在每个抽样位置(也就是2Π/N的整数倍)上的值,就等于X(k)这一点的值,不需要任何其他抽样值参与;而在两个抽样点之间的值(没抽到的地方),需要所有抽样值来参与共同构成。
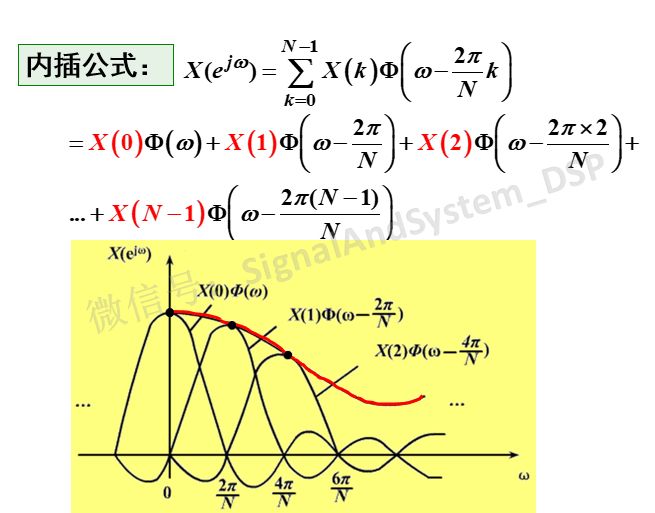
图9
这个问题的理解,与“时域抽样后信号的重建”问题是一样的。但有的同学可能会说,时域抽样后信号的重建,我记得是通过理想低通滤波器来推导出重建的内插公式,这里怎么不是呢?
-
【安富莱——DSP教程】第24章 快速傅里叶变换原理(FFT)2015-06-26 0
-
图像频率域分析之傅里叶变换2019-05-22 0
-
离散傅里叶变换DFT在电阻网络分析中到底起到什么作用2022-08-19 0
-
离散傅里叶变换及其快速算法2008-10-30 842
-
离散傅里叶变换,(DFT)Direct Fouriet Tr2009-07-25 2040
-
有限长离散变换-离散傅里叶变换2011-02-23 1087
-
离散傅里叶变换(DFT)2016-12-28 892
-
离散傅里叶变换(DFT)及其快速算法(FFT)2016-12-28 929
-
数字信号处理第3章-离散傅里叶变换(DFT)2016-12-28 947
-
数字信号处理(第三章-离散傅里叶变换DFT)2016-12-28 987
-
数字信号处理--第3章--离散傅里叶变换(DFT)2016-12-28 980
-
傅里叶变换公式总结2023-09-07 7477
-
傅里叶变换和离散傅里叶变换的关系2023-09-07 2563
-
如何使用DFT进行频谱分析2024-12-20 332
-
DFT与离散时间傅里叶变换的关系 DFT在无线通信中的应用2024-12-20 318
全部0条评论

快来发表一下你的评论吧 !

