ADC中如何确定位数以及有效位数的理解

　　ADC/模数转换器简介

　　模数转换器即A/D转换器，或简称ADC，通常是指一个将模拟信号转变为数字信号的电子元件。通常的模数转换器是将一个输入电压信号转换为一个输出的数字信号。由于数字信号本身不具有实际意义，仅仅表示一个相对大小。故任何一个模数转换器都需要一个参考模拟量作为转换的标准，比较常见的参考标准为最大的可转换信号大小。而输出的数字量则表示输入信号相对于参考信号的大小。

　　分类及特点

　　模数转换器的种类很多，按工作原理的不同，可分成间接ADC和直接ADC。间接ADC是先将输入模拟电压转换成时间或频率，然后再把这些中间量转换成数字量，常用的有双积分型ADC。直接ADC则直接转换成数字量，常用的有并联比较型ADC和逐次逼近型ADC。

　　并联比较型ADC：采用各量级同时并行比较，各位输出码也是同时并行产生，所以转换速度快。并联比较型ADC的缺点是成本高、功耗大。

　　逐次逼近型ADC：它产生一系列比较电压VR，但它是逐个产生比较电压，逐次与输入电压分别比较，以逐渐逼近的方式进行模数转换的。它比并联比较型ADC的转换速度慢，比双分积型ADC要快得多，属于中速ADC器件。

　　双积分型ADC：它先对输入采样电压和基准电压进行两次积分，获得与采样电压平均值成正比的时间间隔，同时用计数器对标准时钟脉冲计数。它的优点是抗干扰能力强，稳定性好;主要缺点是转换速度低。

　　ADC工作原理

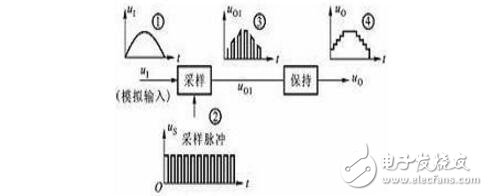
　　输入端输入的模拟电压，经采样、保持、量化和编码四个过程的处理，转换成对应的二进制数码输出。采样就是利用模拟开关将连续变化的模拟量变成离散的数字量，如上图中波形③所示。由于经采样后形成的数字量宽度较窄，经过保持威廉希尔官方网站 可将窄脉冲展宽，形成梯形波，如波形④所示。量化就是将阶梯形模拟信号中各个电压值转化为某个最小单位的整数倍，便于用数字量来表示。编码就是将量化的结果（即整数倍值）用二进制数码来表示。。这个过程就实现了模/数转换。目前集成模／数转换器种类较多，有8位、10位模／数转换器。

　　ADC位数的确定

　　ADC位数是根据传输方式和噪声来计算的。如，64QAM/7/8码率在视频解码正常的最低信噪比为28dB（某种衰落信道下）；OFDM在轻微削波时的峰均比假设为11dB，所以ADC的最大信噪比至少要40dB，考虑信号波动给AGC留出3dB的余量，那么ADC至少要42/6=7位。剩下的就应该是考虑到噪声等因素留的余量了。

　　ADC每增加一位，信噪比提高6dB，前提是输入ADC的波形没有噪声。模拟信号的信噪比是一定的，ADC之后的信号的最高信噪比也就定了。

　　我觉得得分情况。有两点：首先RF指标不可能无限高的；其次，RF指标越高成本越高。对低成本系统，是链路预算决定射频指标，如wlan；对高成本系统，可能是RF指标决定链路预算，如星际通信。

　　选AD，看接收信号的动态范围要求和解调性能的要求。 非线性指标，取决于接收信号的特性以及干扰的特性。

　　ADC有效位数的理解

　　假设一个12位非理想的ADC，其ENOB为10bit，这并不表示把ADC的后两位删掉就可以当做一个理想的10bitADC来使用，如果去掉后两位把该ADC作为一个10bit的ADC来测试，你会发现它的ENOB不到10bit。

　　ENOB的计算方法是使用ADC测量出的SNDR根据公式SNDR=6.02*ENOB+1.76换算而来的，从这个公式我们可以明白这里ENOB的意思是12bit非理想ADC的SNDR与理想的10bitADC的SNR相等。

　　对于一个非理想的ADC，其输出不仅有量化噪声，还有失真引起的高次谐波，所以会在SNDR的计算中抵消一部分精度。

　　信噪失真比 SNDR

　　SNDR是指频带内信号总功率和噪声以及谐波功率之和的比值。它的定义和SNR的定义类似，只是为了强调ADC中的谐波失真。

　　ADC的有效位数与有效分辨率的区别

　　ADC的分辨率位数（N）可决定ADC的动态范围（DR），其代表ADC可测量的输入信号等级范围，通常以［dB］为单位。DR可定义为：

　　

　　请注意，由于信号在给定时间视窗内的RMS幅值取决于信号幅值在该时间视窗内如何变化，因此ADC的DR变化取决于输入信号特征。对于其满量程范围（FSR）内的恒定DC输入而言，理想的N位ADC可分别测量FSR和FSR/2N的最大及最小RMS幅值。因此，ADC的DR为：

　　

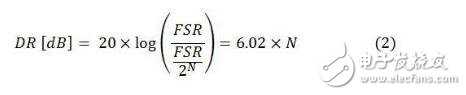
　　同理，对于幅值随ADCFSR变化而变化的正弦波信号输入而言，理想的N位ADC可测量（FSR/2）/√2的最大RMS幅值。正弦波输入信号的最小可测量RMS幅值受量化误差的限制，其近似于幅值为半个LSB或FSR/2N+1的锯齿波。幅值A的锯齿波RMS幅值为A/√3。因此，正弦波输入信号的理想ADC的DR是：

　　

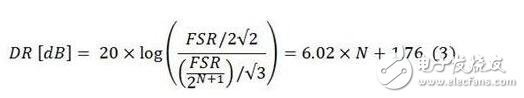
　　真正的ADC具有可降低DR的误差。事实上，根据输入信号特征的不同，在输入信号接近其最小值时，ADC输出有不同类型的误差占主导地位。

　　对于恒定DC输入而言，ADC的输出误差主要取决于所谓的“过渡”噪声，其包含ADC、ADC驱动器以及电源等组件的固有宽带散热噪声。如果ADC不存在较大的线性（DNL）问题，过渡噪声可在ADC输出端产生一个近似高斯代码分布。

　　

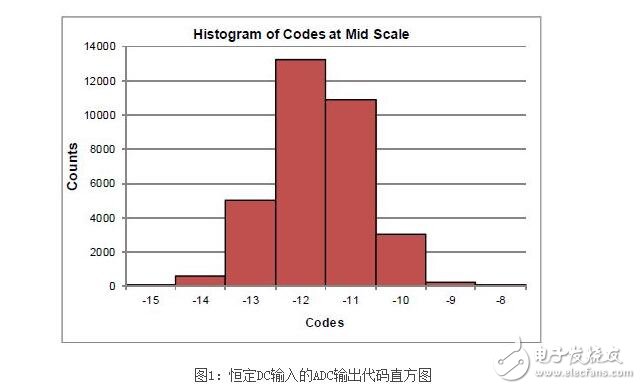
　　本直方图的一个标准偏差（σHISTO）相当于过渡噪声的RMS值。在σHISTO》1LSB时，ADC的DCDR就会减小至：

　　

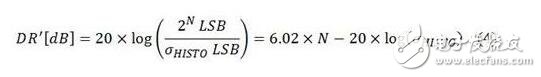
　　将（2）和（4）组合起来，可重新计算出降低的分辨率或有效分辨率：

　　

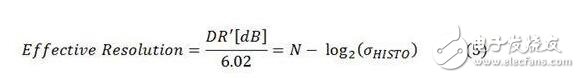
　　同理，对于时间变化的输入而言，ADC的输出包含动态误差（即量化噪声与失真）以及可降低DR的过渡噪声。改变后的DR通常被称为SINAD，重新计算的ADC分辨率被称为ENOB。因此：

　　

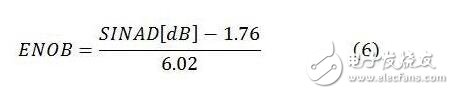
　　总之，给定ADC可能具有不同的DR和分辨率，主要取决于输入是AC（交流）还是DC（直流）信号。因此，ADC分辨率有单独的衡量指标，其对应于不同的输入条件，即ENOB对应于AC（交流），有效分辨率对应于DC（直流）输入。确定哪种更适合自然取决于您的应用。