
资料下载

×
小波处理在DSP Builder的脑电信号处理解析
消耗积分:1 |
格式:rar |
大小:0.4 MB |
2017-10-26
1 引言
脑电信号EEG(Electroencephalograph)是人体一种基本生理信号,具有重要的临床诊断和医疗价值。南于脑电信号自身具有非平稳性随机的特点,因此,对其实时滤波具有相当难度。自从Berger 1929年发现脑电信号以来,人们采用多种数字信号处理技术处理分析脑电信号,由于传统的滤波去噪方法所用滤波器一般具有低通特性,因此采用经典滤波法对非平稳信号去噪,降低噪声,展宽波形,平滑信号中突变尖峰的成分,但可能损失这些突变点携带的重要信息,而傅里叶频谱分析仅是一种纯频率分析方法,该方法对时变的非平稳脑电信号无效。
与传统的傅里叶变换相比较,小波变换是一种多尺度信号分析方法,具有良好的时频局部化特性,非常适合分析非平稳信号的瞬态特性和时变特性,这正是分析 EEG所需要的,EEG中许多病变都是以瞬态形式表现的。只有结合时间和频率进行处理,才能取得更好效果。但小波分解每次只分解上次分解的低频部分,而不分解高频部分,所以高频段分辨率较差。而小波包分解是一种从小波分解延伸出的更细致的分解和重构信号的方法,它不但分解低频部分,而且还能二次分解高频部分,能够很好地将频率分辨率调整到与脑电节律特性相一致,因此小波包分解具有更好的滤波特性。若将小波包方法引入脑电信号分析.不仅可以克服传统脑电分析的不足.还可以改进Mallat算法分析实际脑电中的不足。
脑电信号的数字处理以往采用通用PC机或单片机实现,存在实时性差等缺点。随之,基于FPGA的小波变换在脑电信号数字处理中应运而生,其实时性好。 DSP Builder将Matlab/Simulink设计仿真工具的算法开发、模拟和验证功能和Quartus II软件的HDL综合、模拟和验证功能相结合,为小波变换的FPGA提供良好的平台。
2 一维离散小波(1D-DWT)Mallat改进算法
多分辨率分析是小波分析的核心理论,其Mallat算法是信号小波分解和重构的常用算法。正交小波的分解和重构公式由尺度函数的尺度方程系数确定。假设构造正交小波的尺度函数φ(t)的两尺度方程为:
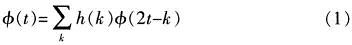
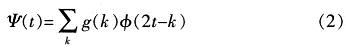
式中,g(n)=(-1)n-1h(2N-n-1),N为自然数常数。
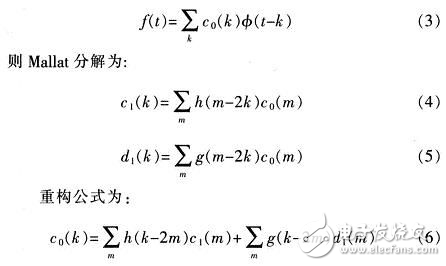
脑电信号EEG(Electroencephalograph)是人体一种基本生理信号,具有重要的临床诊断和医疗价值。南于脑电信号自身具有非平稳性随机的特点,因此,对其实时滤波具有相当难度。自从Berger 1929年发现脑电信号以来,人们采用多种数字信号处理技术处理分析脑电信号,由于传统的滤波去噪方法所用滤波器一般具有低通特性,因此采用经典滤波法对非平稳信号去噪,降低噪声,展宽波形,平滑信号中突变尖峰的成分,但可能损失这些突变点携带的重要信息,而傅里叶频谱分析仅是一种纯频率分析方法,该方法对时变的非平稳脑电信号无效。
与传统的傅里叶变换相比较,小波变换是一种多尺度信号分析方法,具有良好的时频局部化特性,非常适合分析非平稳信号的瞬态特性和时变特性,这正是分析 EEG所需要的,EEG中许多病变都是以瞬态形式表现的。只有结合时间和频率进行处理,才能取得更好效果。但小波分解每次只分解上次分解的低频部分,而不分解高频部分,所以高频段分辨率较差。而小波包分解是一种从小波分解延伸出的更细致的分解和重构信号的方法,它不但分解低频部分,而且还能二次分解高频部分,能够很好地将频率分辨率调整到与脑电节律特性相一致,因此小波包分解具有更好的滤波特性。若将小波包方法引入脑电信号分析.不仅可以克服传统脑电分析的不足.还可以改进Mallat算法分析实际脑电中的不足。
脑电信号的数字处理以往采用通用PC机或单片机实现,存在实时性差等缺点。随之,基于FPGA的小波变换在脑电信号数字处理中应运而生,其实时性好。 DSP Builder将Matlab/Simulink设计仿真工具的算法开发、模拟和验证功能和Quartus II软件的HDL综合、模拟和验证功能相结合,为小波变换的FPGA提供良好的平台。
2 一维离散小波(1D-DWT)Mallat改进算法
多分辨率分析是小波分析的核心理论,其Mallat算法是信号小波分解和重构的常用算法。正交小波的分解和重构公式由尺度函数的尺度方程系数确定。假设构造正交小波的尺度函数φ(t)的两尺度方程为:
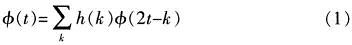
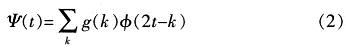
式中,g(n)=(-1)n-1h(2N-n-1),N为自然数常数。
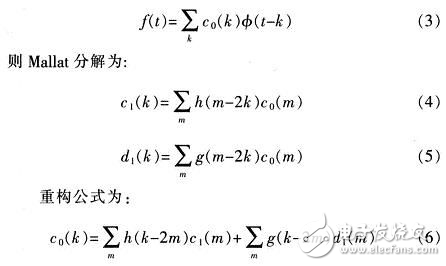
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
评论(0)
发评论
- 相关下载
- 相关文章






