

基于旋转体矩量法的天线设计
RF/无线
描述
在分析口径较小,焦距较短,带有复杂结构馈源的毫米波反射面天线时,不再适合采用高频近似方法,而采用全波矩量法求解,由于其巨大的计算量在PC机上求解还有很大的困难,提出一种计算毫米波反射面的新方法,充分利用计算模型轴对称这一几何特性,建立旋转体矩量法模型,并把该方法应用到设计微波传输系统中的小口径毫米波反射面天线上。由于在建模中考虑了馈源和主抛物面之间的互耦,计算结果和实验结果相当吻合。通过理论分析和实验,设计的口径为O.3 m天线在整个角域上满足了特定的方向图包络,达到了ETSI Class 3的高性能标准。
随着人们对无线通信品质的需求越来越高,多层次的通信系统逐步建立起来。为了使各系统或子系统能够紧密结合起来,稳定高速率的数据传输系统是很有必要的。以毫米波天线为基础的微波传输系统由于其成本较低,易于施工等特点受到人们的青睐。该系统要求毫米波天线满足严格的方向图包络和良好的交叉极化分辨率,一直以来成为天线设计的热点问题之一。反射面天线的设计方法基本上是几何光学和物理光学等高频近似方法。对于电大尺寸的反射面天线,用这种方法分析计算是合理的。对于口径较小,馈源结构比较复杂的反射面天线,高频方法显然不适合应用。文献[1]在馈源上采用低频方法,如矩量法、FDTD等,在反射面天线上则采用高频方法,计算在较小的主瓣附近区域内的方向图,得到比较合理的结果,但是由于没有考虑到馈源系统与主反射面互耦等效应的影响,对于大角度区域,其结果往往和测量结果差别很大。微波传输系统要求的微波传输天线,经常是口径小,焦距比短的毫米波反射面天线,且在全空间满足一定的方向图包络要求。由于这类天线不能满足高频方法要求的电大尺寸条件,且要求分析方法能对天线的远副瓣和背瓣精确的求解,故而高频近似方法不能用于该类问题的求解。目前,采用矩量法分析电大尺寸和复杂结构的研究是计算电磁学的热点问题,特别是文献[6]采用综合函数法与矩量法相结合,把复杂结构分为几块,对每块进行依次求解,虽然使矩量法不能求解的问题得到解决,但求解时间仍然很长。
本文采用矩量法,充分利用轴对称反射面天线的几何结构这一特性,采用旋转体矩量法(BOR MoM)进行求解,使三维问题转化为二维问题。目前,采用旋转体矩量法设计小口径反射面天线得到了重视。文献[8]采用旋转体矩量法设计了小口径微波天线,设计频率为5 GHz,理论结果和实验结果吻合的很好。本文把旋转体矩量法应用到毫米波天线上,这在以往文献上还比较少。实验证明,这种方法能够有效分析具有轴对称结构的反射面天线,解决了高性能微波传输天线的分析设计问题。
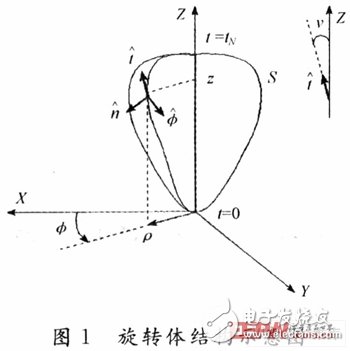
1 旋转体矩量法(BoR MoM)
所谓旋转体,是由母线绕旋转轴旋转一周得到的物体,其结构参数如图1所示。其中,ρ,φ和z为柱坐标的3个分量;t为母线的长度;t,φ分别是S上任一点沿t和φ增加的方向;n=φt;v为t和z轴的夹角。对于散射或辐射问题,经常转化为计算电磁场的边值问题,采用电场积分方程或磁场积分方程。本文在推导矩阵方程的时候采用的是电场积分方程。对于良导体,边界条件为:
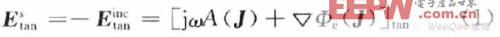
式中:Etan inc是入射电场的切向分量;Etan s为散射电场的切向分量;J为良导体上的感应电流。令L算子为:
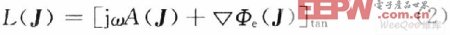
由于所求解
的物体为轴旋转体,则求解电流在φ方向是以2π为周期的周期函数,则用基函数t‘fi(t’)和φ‘gi(t’)展开,可以表示为:
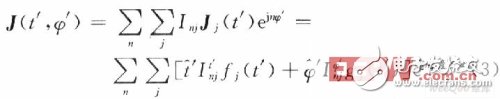

采用咖略金方法,所用与基函数相同的检验函数,Wmlt=tfl(t)ejmφ,Wmlφ=φgl(φ)ejmφ,对式(6)两边和检验函数求内积,得:
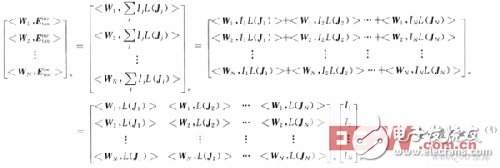
由于傅里叶级数的正交性,只有m=n时,式(7)的内积不为零。式(7)扩展成矩阵的形式则为:
即:

- 相关推荐
- 天线
-
求助:矩量法计算偶极子天线输入阻抗不正确2021-01-14 0
-
高速飞行的旋转体姿态识别技术研究2009-05-10 787
-
基于AutoCAD平台的旋转体拉伸毛坯计算机系统的开发2009-08-24 408
-
纺织设备中金属旋转体振动的单片机测试系统2010-07-14 393
-
基于μCOS-Ⅱ的旋转体非接触测温系统2010-07-27 396
-
于矩量法对一种手机天线的特性分析2010-09-06 399
-
NFM盾构机的主传动轴旋转密封系统详细资料说明2019-06-25 969
-
利用旋转磁铁产生ELF无线电信号的实验研究2020-04-20 891
-
基于旋转体矩量法的高性能微波传输天线分析与设计2020-08-11 593
-
如何使用全波矩量法(MoM)技术分析天线步骤2023-08-01 1371
全部0条评论

快来发表一下你的评论吧 !

