

FPGA加速N粒子重力并行模拟实现和仿真案例
描述
通过使用以200 MHz运行的8个并行浮点加速器,展示小型ZU3EG SoC的科学计算能力。
硬件元件
96Boards Ultra96 ×1
Avnet AES-ACC-U96-PWR ×1
USB Cable Assembly, USB Type A Plug to Micro USB Type B Plug ×1
Mini displayport cable ×1
Micro SD card (Must be 8GB or larger)×1
DisplayPort monitor ×1
USB Mouse (Optional) ×1
USB Keyboard (Optional) ×1
软件App与线上服务
Xilinx Vivado Design Suite
Avnet Ultra96 Pynq image v2.4
介绍
牛顿物理描述了我们宇宙中的行为和非常大的物体/粒子。根据某些假设,这些定律可以应用于天文尺寸到高尔夫球(甚至更小)尺寸的物体/粒子。不同粒子之间的相互作用由以下的重力方程控制。
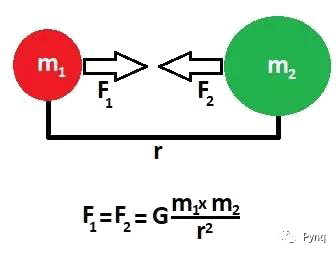
在N粒子系统中,每个粒子经受了其他(N-1)个粒子的力。力的组合结果导致了所述粒子的加速。类似地,所有其他(N-1)个粒子同时经历了系统中其他粒子对它作用的力。所得到的的所有粒子的加速度,结合空间里的初始位置,初始速度和时间不长分别得到所有N个粒子的新位置。为了简化模型的实现,做出了以下的假设:
1. 所有粒子都是点质量(质点模型)
2. G=1
3. 在重力计算中引入一个修正系数,以避免当两个点质量处于完全相同的坐标时候产生的误差。
该设计已经实现通过python软件加载16bit正负整数格式的初始坐标、质量、修正系数和模拟时间步长。尽管Vivado环境中提供了浮点数的加法、减法和乘法,但我们还是努力设计自定义浮点数格式。
设计:概念证明
该算法采用python软件实现和仿真,以下是硬件实现之前在PC上进行粒子模拟的主要算法和屏幕截图。
由于迭代过程,该算法具有O(N2)的计算复杂度。这是在硬件中实现加速器的绝佳机会。您可以尝试使用nbody_x86.py来查看粒子模拟在软件中的运行速度。使用硬件实现的加速器可以更快地运行粒子模拟。
该算法可被矢量化,因此如果使用矢量处理器,复杂度将会降低到O(N)。下面的示例是识别计算密集型算法的关键部分,并在fabric/PL中为它们提供加速器。
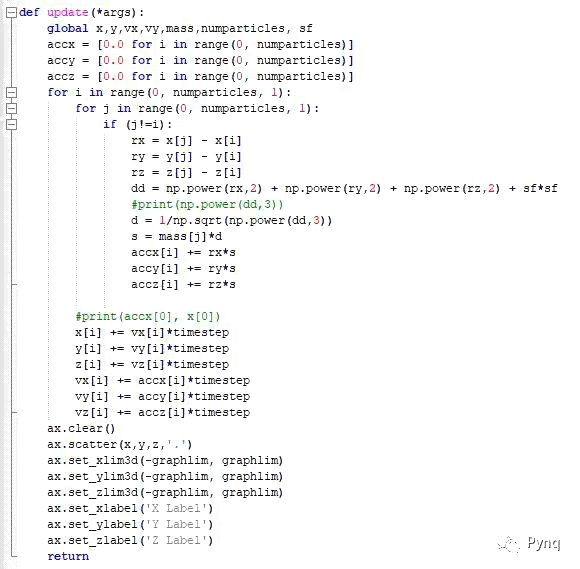
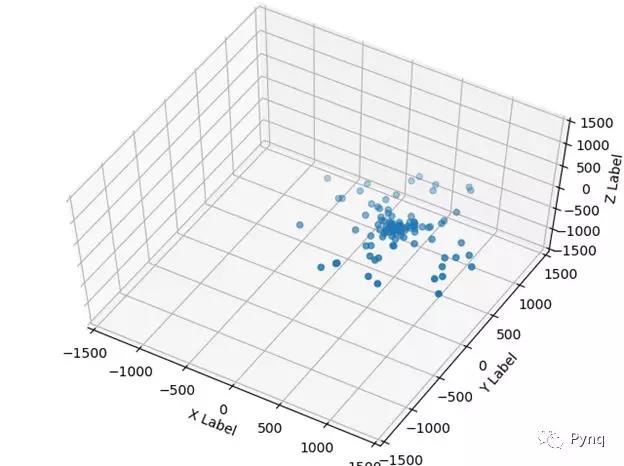
假设在t0时刻,所有粒子的位置和速度信息都是已知的。
考虑双粒子系统。由第二个粒子引起第一个粒子的加速度计算如下:
a = (G*m2)/(r^2)n
为了保持加速度的方向信息:a = (G*m2*|r|)/(r^3)
N 物体问题:
1.上述概念可以扩展到N个物体的体系。
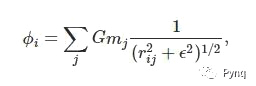
2.在GRAPE-[x]中,修正系数“ε”用于研究尺寸的详细影响。对于此项目,is设置为0。
3.另一个修正系数用于防止不同的颗粒彼此非常接近,即防止“r~=0”,如上面python软件中的变量“sf”所示。
硬件设计
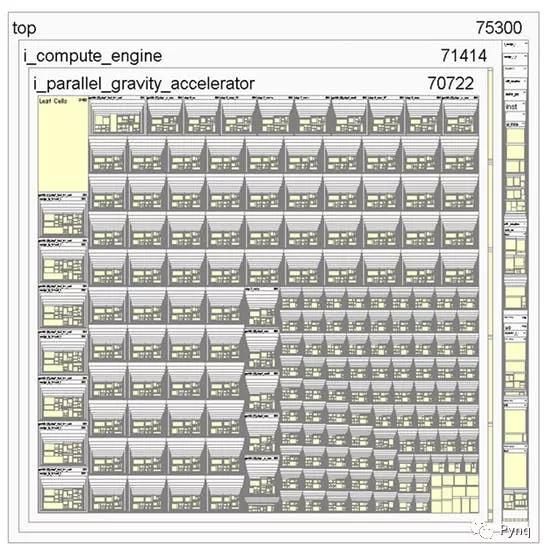
该设计采用8个并联加速器发动,可完全支持多达4000多个物体并行模拟。
使用8个并行加速器的实现
最初的设计有一个加速器以75MHz运行。并联增加7个加速器是的工作频率增加了一倍以上,功耗增加了约1W。一个加速器的数据将在后面的部分中显示,此表给出了8个并联加速器的数据。
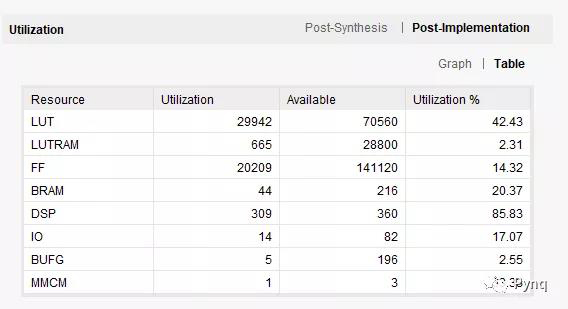
性能
针对4000个粒子,该设计满足了200MHz的定时!通过添加管道修改了浮点加法和乘法。
仅使用200MHz的加速器实现 - 数据比较
尽管逻辑复杂,但实现在XCZU3EG上使用一个单重力计算引擎消耗了以下资源。一个重力引擎可以计算1024个粒子之间的相互作用(由输入和输出的BRAM深度决定)。定时器成功关闭在200MHz。流水线技术在重力引擎中实现。在每个本地模块中重置流水线以实现优化全局重置绕线传播。整个设计在单个时钟源上运行。
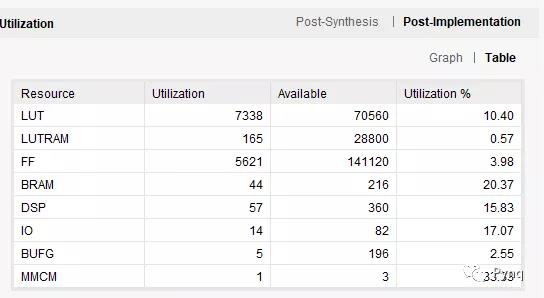
浮点计算
由于科学计算中的数字从极小的数值到天文大值,IEEE754 FP32是浮点数计算的初始选择。在IEEE754 FP32中,数字由1个符号位,8个指数位和23个尾数位表示,如图所示:

然而,DSP48E2只能执行27bx18b的乘法运算。 因此,选择使用仅具有18个尾数位的自定义浮点表示。 因此,该设计中的浮点运算使用27b浮点表示。
可以这种格式表示的最小数字:+/- 1.000000000000000001 x 2 **(- 126)
可以此格式表示的最大数字:+/- 1.111111111111111111 x 2 **(127)
指数偏差为127
NaN,溢出和下溢的IEEE 754条件尚未最大限度地实施。
FP算法实现
实现了基于IPI的浮点运算。 为了有效使用DSP48,浮点数的加,乘法被限定为27位,而由于限制,浮点数的逆平方根被固定为单精度浮点表示法。 int16到浮点数,浮点数到int16也是使用Xilinx IP完成的。
流程图
下图显示了RAM,计算引擎,流水线重力引擎等的最高层视图。
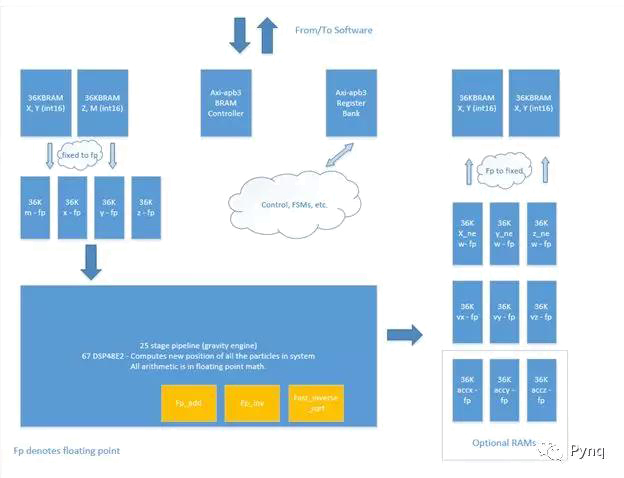
重力引擎
重力引擎是设计的核心。 它是按照上图所示的算法实现的。下图显示了重力引擎和所有15个管道的实现细节。
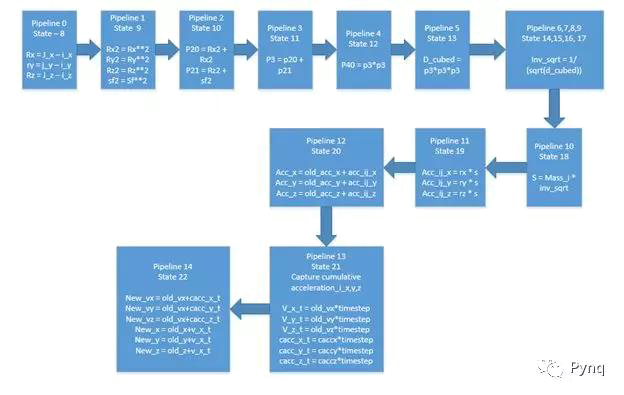
控制和状态登记; 地址空间
所有BRAM均使用基于APB3总线的RTL开发的BRAM控制器进行控制。 AXI -APB3桥在块设计中实例化。 类似地,实现了另外的APB控制和状态寄存器组以便控制计算引擎。
以下是地址段和寄存器空间:
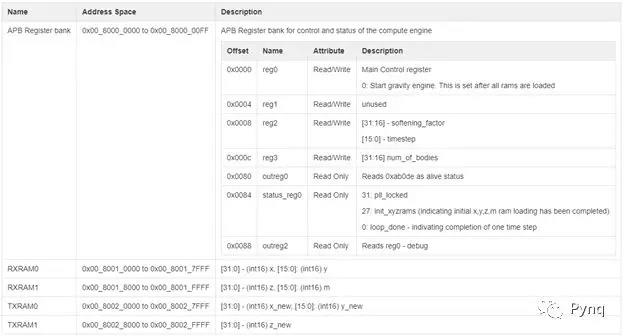
设计层次结构
i_design_1是PS系统,i_compute_engine是PL部分中实现的硬件设计。
软件流程
Python软件是在PYNQ框架上编写的,用于按顺序执行以下操作:
1. 计算系统中N粒子的x,y,z,m的初始条件,修正系数和模拟时间步长。
2. 通过将int16的x,y,z,m值加载到BRAM中来配置计算引擎
3. 启动计算引擎
4. 等待计算引擎完成一个时间间隔的步骤
5. 从TXRAM中检索新的x,y,z
6. 使用DisplayPort模块创建DisplayPort框架。 将帧归零,使用新数据加载帧并将帧写入监视器。
7. 重复!
DisplayPort配置为1280 x 720像素
粒子的新位置可能远远超出显示器尺寸。它们只是没有显示。
编辑:hfy
-
上海交大π2.0超算实现天文学N体模拟粒子数的新记录2020-03-17 1991
-
如何使用FPGA实现全并行结构FFT2021-03-31 1075
-
并行3维全电磁粒子模拟软件NEPTUNE的外加磁场模块设计2010-05-13 0
-
真心求助,基于FPGA的重力感应赛车游戏的一些问题2013-03-21 0
-
加速传感器(重力感应)2016-07-13 0
-
Z轴加速度去除重力影响原理是什么2019-07-05 0
-
重力加速度的研究2008-11-24 2365
-
基于FPGA的ARM并行总线设计与仿真分析2013-08-15 7962
-
基于FPGA的软硬件协同仿真加速技术2014-03-25 5345
-
基于FPGA的ARM并行总线研究与仿真2017-01-24 868
-
DSP并行系统的并行粒子群优化目标跟踪2017-10-20 738
-
改进模拟退火与粒子群混合算法2017-11-30 898
-
无与伦比的并行处理—FPGA加速的根本基石2023-09-15 145
-
粒子加速器的加速原理是啥呢?2023-12-18 2103
-
用DE1-SOC进行硬件加速的2D N-Body重力模拟器设计2024-04-09 558
全部0条评论

快来发表一下你的评论吧 !

