

关于Monte Carlo仿真的降低光谱散射方法比较研究
电子说
描述
0 引言
由于不同物质对于不同波长光波的吸收和散射的响应不同,光谱技术被广泛应用于各种物质属性的分析与检测[1]。然而不同物质的非均匀性与高度散射特性是造成光谱检测与分析结果不准确的主要原因。散射导致穿过介质的光子光程大于光源与光检测器的距离,同时光谱分析的基本线性定律,即朗伯比尔定律(Lambert-Beer law,A=μa d)不再成立。
如果能够克服光子在介质中散射的问题,则可以极大地提高光谱检测的精度和应用范围。所以,在光谱检测分析中大量使用了降低散射的方法用于提取出弱散射的光子,达到最终提高光谱检测精度的目的[2-4]。然而提取弱散射光子的同时必然会降低检测到的光信号的强度,即影响检测的信噪比。所以在应用降低散射方法提高精度与保证检测信号的信噪比之间要做权衡。
本文应用Monte Carlo模型[5]对3种在光谱技术中常用的降低散射的方法进行了比较分析,即偏振差法[2]、附加吸收剂法[3]和空间滤波法[4]。这3种方法都用于提取出弱散射光子,其基本思路是弱散射光子的光程等于或接近光源与光检测器距离,从而基于朗伯比尔定律可以得到光强衰减与光子吸收系数之间的近似线性关系。本文对于线性化的效果通过比较光程的方差来判断,对于不同方法在获得相似的光程方差的同时的检测光强也进行了比较。
1 原理
1.1 光子吸收和散射与光强衰减的关系
由于介质对光的散射和吸收,光波穿过介质后强度发生衰减。吸收导致透射光强度的减少,散射造成透射光在空域和时域的发散。由于光检测器尺寸和检测角度的有限性,散射也导致了检测光强的衰减。标志介质对光的吸收和散射程度的参数为吸收系数(μa)和散射系数(μs),二者均与光波波长相关。
朗伯比尔定律是光谱分析的基本定律[1],在不存在散射的情况下,透射光光强的衰减(Attenuation,A)与介质的吸收系数之间存在线性关系,即:

其中I0是入射光强,I是穿过介质的透射光强,二者的关系为:
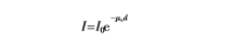
,d是光子在介质中经过的光程长度,本文以毫米为单位。对于透射光谱检测技术,光源与光检测器通常共轴放置,所以在没有散射的情况下,透射光程为常数,即等于介质的厚度,A与μa成线性关系,如式(1)所示。此外,光子光程的方差为零。当存在散射的情况下,散射导致光子光程为不定长的变量。所以,散射导致A与μa关系成非线性。
散射导致光子光程超过光源与光检测器间距离,从而导致光检测器检测到的光子在时间上展宽。通常用出射光的时间响应曲线(Temporal Point Spread Function,TPSF)反映光子在介质中光程。图1显示当光子穿过充满散射介质时,透射光的TPSF时间响应曲线展宽(图1(b)),光强衰减与吸收系数为非线性关系(图1(c)),光程方差不再为零(图1(d))。光程方差值越小,意味着光子散射程度越低,光强衰减与吸收系数间更加线性化。所以本文以光子光程的方差作为评价散射降低方法效果的依据。

1.2 降低光谱散射方法
偏振差法是一种有效的去除散射光的方法,广泛应用于光谱检测[2]、光学成像[6]、多层介质特性研究[7]等领域。偏振差法的基本思想是基于弱散射光的偏振保持特性。散射导致光子的偏振状态呈现随机化,因此多次散射光呈现随机偏振状态。所谓偏振差法,即是在光检测端加入一个与入射光偏振方向一致的偏振片检测出保持原有偏振态的部分光,再应用一个与入射光偏振方向正交的偏振片检测出多次散射的部分光,将二者相减提取出弱散射光[2]。
在光谱测量中使用附加吸收剂法[3]是通过加入一定可控数量的吸收剂,使多次散射光进一步衰减,达到A与μa进一步线性化的目标,最终提高光谱测量的精度。本文应用附加吸收剂法滤除光程较长的多次散射光。
对于传输光谱,应用空间滤波法是基于弱散射光更靠近光轴,而强散射光更加远离光轴的基本思想。因此共轴放置光检测器与光源,可以获得弱散射光。Leith[8]等人证明在传输模式下,通过控制光检测器的检测尺寸可以得到弱散射光信号,即包含无散射光子和弱散射光子的光信号。
1.3 Monte Carlo模型
由于Monte Carlo方法可以使仿真光子在不同介质中的传输过程更加灵活,因此得到了广泛的应用。本文采用Monte Carlo方法[5]仿真透射光穿过充满散射介质的试管的过程,并且对每个光子在传输过程中的散射、吸收以及偏振态的改变进行独立计算,文中共仿真5×107个光子。充满散射与吸收介质的试管尺寸设定为(40×10×10)mm3,光子从侧面(40×10 mm2)中心正入射进入试管。
假定以生物研究为光谱分析与检测的对象[9],介质的散射和吸收系数范围设定为μs=2~9 mm-1与μa=0~0.3 mm-1,其各向异性系数(散射角余弦的平均值)g=〈cosθ〉=0.9。仿真过程中每个光子每次散射的步长、散射角度、位置、偏振态都会被计算并且记录下来。
光子偏振态的改变基于Muller矩阵与Stokes矢量进行计算。对于空间滤波法的仿真,只有所有符合光检测器检测尺寸与检测角度的光子会被用于计算出射光强。本文假定光检测器为圆形,尺寸为2 mm,检测角度设定为5°。对于附加吸收剂法的仿真,是通过计算所有出射光子的总光程,再应用朗伯比尔定律计算光强,附加吸收剂的吸收系数表示为μaadded。
2 仿真结果与分析
2.1 弱散射系数情况下的3种方法比较
图2显示了在散射系数μs=2 mm-1情况下的TPSF时间响应曲线(图2(a))、吸收系数μa与光强衰减A(图2(b))以及与方差(图2(c))的关系曲线。每幅子图中包含4条曲线,即未应用任何降低散射方法的透射光的响应曲线(实线),以及应用圆偏振差法(短划线)、附加吸收剂法(点划线)、空间滤波法(虚线)曲线。从图2可以看出,加入降低散射方法可以得到更窄的TPSF曲线(图2(a)),使光强衰减与吸收系数关系曲线更加线性化(图2(b)),以及得到更低的光程方差(图2(c))。但是,从图2(a)和图2(b)中更高的衰减值可以看出,降低散射法的光强衰减也更为严重。
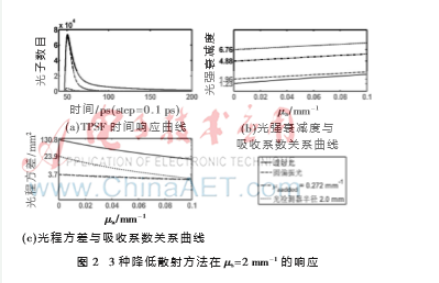
附加吸收剂法是通过添加可控剂量的吸收剂,使多次散射的长光程光子被进一步衰减,从而实现降低光子光程总长度的目标。为了更好地与偏振差法相比较,附加吸收剂剂量控制在0.272 mm-1,即可以获得与偏振差法相近的光程方差与线性化程度。然而,附加吸收剂法检测到的光强更弱,光强衰减度更高,意味着信噪比更低。值得注意的是附加吸收剂法的效果取决于添加的附加吸收剂的多少,继续增大附加吸收剂会使线性化程度更好,但是也会影响输出的光强值。
空间滤波法滤除了多次散射的光子,使检测到的光子光程近似等于光源到光子检测器距离。所以,应用空间滤波法可以线性化光强衰减度与吸收系数关系曲线。与偏振差法相比,空间滤波法获得的透射光TPSF尽管更窄,但是由于仿真噪音的影响,光子分散程度更高,所以方差值更大。3种方法中空间滤波法的光强衰减最为严重。同样,空间滤波法的效果取决于光检测器的尺寸。增大光检测器尺寸,可以提高检测光强,但是会影响提取弱散射光子的效果。
3种方法中,偏振差法获得的检测光子数目最高(图2(a)),光强衰减度最低(图2(b)),光程方差最低,即获得光子发散程度最低(图2(c))。所以,偏振差法相比其他两种方法效果更好。
2.2 提高散射系数情况下3种方法比较
在散射系数比较低的情况下(μs=2 mm-1),相比附加吸收剂法和空间滤波法,偏振差法可以检测到光强更强、分散程度更低的弱散射光子。以下对提高散射系数情况下的3种方法的效果进行比较分析。图3、图4、图5显示了在散射系数μs=4、7、9 mm-1情况下,3种方法的响应。
随着散射系数的增加,偏振差法仍旧可以提取出弱散射光子,但是偏振态保持特性在降低。偏振差法提取出的光子数目也随之减少,衰减增加。图3(a)中TPSF尾部的噪音主要来自于随机噪声。在高散射情况下,散射导致光子光程拉长,TPSF尾部拉长,曲线平滑度降低(图3(a)),光程方差随μs增加而增加(图3(c))。同样,散射导致光强衰减增加,如图3(b)所示。当μs》9 mm-1之后,无法获得满意的偏振保持曲线,所以文中仿真到μ=9 mm-1。
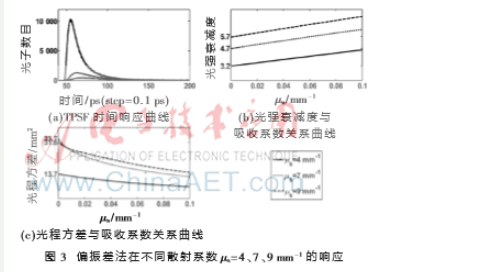
图4显示了附加吸收剂法在不同散射系数下的响应。为了便于与偏振差法相比较,附加吸收剂的取值使附加吸收剂法与偏振差法取得一致的光程方差值(图3(c)和图4(c))。则相应附加吸收剂的值分别为:μaadded=0.199 (实线)、0.158(虚线)和0.133 (短划线) mm-1。比较图3(b)和图4(b)中的光强衰减值可以看出,与偏振差法相比,附加吸收剂法提取出的光强更弱。

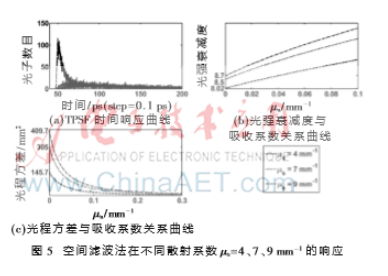
图5显示了空间滤波法在不同散射系数取值下的响应。同样,随着μs的增加,TPSF噪声增大(图5(a)),方差增加(图5(c)),光强衰减度也随之增加(图5(b))。相比于偏振差法,空间滤波法所获得的光强更弱。这与选取的检测器的尺寸大小相关,为保持一致,此处仍旧取光检测器尺寸为2 mm-1。
2.3 3种方法的检测光强的比较
提取出弱散射光子,不可避免地降低了检测光的强度。在应用降低散射方法的同时,还要权衡对于光检测强度的影响。所以文中对3种方法在获得相同光程方差值处的光检测强度进行了比较。
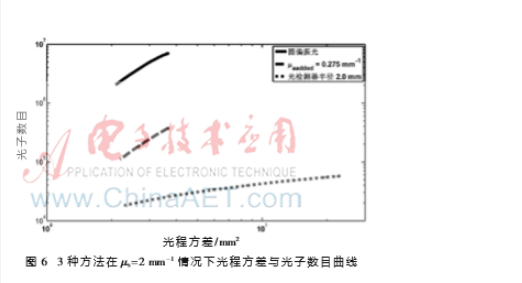
图6给出了3种方法在散射系数μs=2 mm-1时的光程方差与光子数目的关系曲线。光子数目对应光检测器检测到的光强。相同方差的情况下,光子数目值越高,说明该方法的性能越好。可以看出在当前散射系数条件下,偏振差法(实线)给出了最佳的性能,其次是附加吸收剂法(短划线)和空间滤波法(虚线)。
3 结论
本文以提高光谱检测精度为目标,以光谱分析的基本线性定律——朗伯比尔定律为理论基础,对3种常用的降低光谱散射的方法进行比较分析。以线性化光强衰减度与吸收系数的关系曲线,缩短光程方差作为评价各种方法的标准。根据本文的仿真,相比于附加吸收剂法和空间滤波法,偏振差法给出了更好的线性化效果,更低的光程方差,可以更加有效地提高光谱检测的精度。此外应用降低散射的方法不可避免地导致检测光强的降低。文中比较了3种方法在相同光程方差情况下的光强,仿真结果表明,偏振差法给出了最佳的线性化光谱分析的效果,同时可以获得最高的检测光子数目。
参考文献
[1] PARSON W.Modern optical spectroscopy[M].New York:Springer,2007.
[2] LU B,WU J W.Quantifying spectroscopic concentration ratio by polarization subtraction technique[J].Chinese Optics Letters,2013,11(S2):S23001.1-4.
[3] REICH O,SCHAEL F.Investigation of the optical diffusion coefficient in turbid media by the added-absorber method[C].European Conference on Biomedical Optics,2001,4431:299-305.
[4] EVERALL N.Temporal and spatial resolution in transmission raman spectroscopy[J].Applied Spectroscopy,2010,64(1):52-60.
[5] CHANG P C Y.Polarization discrimination for active imaging in scattering media[J].Optics Communications,1999,159(1-3):1-6.
[6] ZHU Q.Experimental and theoretical evaluation of rotating orthogonal polarization imaging[J].Journal of Biomedical Optics,2009,14(14):034006.1-10.
[7] STOCKFORD I M.Analysis of the spatial distribution of polarized light backscattered from layered media[J].Journal of Biomedical Optics,2002,7(3):313-320.
[8] LEITH E N.Realization of time gating by use of spatial filtering[J].Applied Optics,1999,38(8):1370-1376.
[9] SANDELL J L,ZHU C T.A review of in-vivo optical properties of human tissues and its impact on PDT[J].Journal of Biophotonics,2013,4(11-12):773-787.
编辑:jq
-
二维和三维Gauss随机粗糙面的Monte Carlo仿真2010-05-28 0
-
驻相近似下二维海面后向散射增强效应研究2010-05-28 0
-
[求助]ORCAD16.2 的完全破解方法2010-06-03 0
-
如何使用蒙特卡罗方法设计领域驱动的设备云?2021-05-25 0
-
请问怎样用比较器对ac进行仿真?2021-06-25 0
-
基于Monte Carlo的非测距传感器网络定位算法2009-04-06 586
-
降低OFDM信号峰均比方法的研究及仿真2009-08-29 683
-
应用G语言平台LabVIEW进行Monte Carlo模拟实2009-09-23 377
-
海面散射仿真中不同波浪谱和松弛率模型选取的对比研究2010-02-09 498
-
基于MATLAB仿真的火电厂环境影响的研究_张新铭2017-03-18 715
-
光伏系统直流失配损失与仿真方案2023-06-01 3159
-
一文解析拉曼散射和光谱学2024-03-29 1118
-
地物光谱仪的两种天空光测量方法比较2024-07-29 421
-
拉曼光谱的原理及其应用2024-08-26 347
全部0条评论

快来发表一下你的评论吧 !

