基于深度学习立体匹配的基本网络结构和变种

深度学习立体匹配之 MC-CNN中两种结构：MC-CNN-fst和MC-CNN-acrt。这两个算法由Zbontar和LeCun共同研发，分别代表了速度与精度的平衡。MC-CNN-fst关注于快速处理，而MC-CNN-acrt则更注重匹配精度。这两种算法为深度学习立体匹配技术的发展奠定了基础，而从效果上看他们明显超过了当时很多优秀的立体匹配算法，成为了SOTA。我们先看看当前的学习地图：

学习进度地图 那么在本篇文章中，我将更深入地探讨基于深度学习的立体匹配算法，涉及一系列有趣的网络结构和变种。我会带你首先回顾这两个算法的基本架构，然后讨论如何通过网络变种、训练策略、正则化和视差估计等技巧来进一步提升它们的性能。这篇文章旨在帮助大家全面地了解深度学习立体匹配算法的发展现状和研究趋势。今天的文章大量参考引用了参考文献[1]，再次对作者表示敬意！ 1. 基本网络结构回顾

1.1 网络架构回顾

下面是我上次提到的Zbontar和LeCun[2][3]提出的两种算法的架构图，这是是深度学习立体匹配领域最基础的结构。其中一个被作者命名为MC-CNN-fst，另外一个则命名为MC-CNN-acrt，其后缀fst和acrt分别代表fast和accurate，顾名思义MC-CNN-fst追求的是计算效率，而MC-CNN-acrt追求的则是准确性。

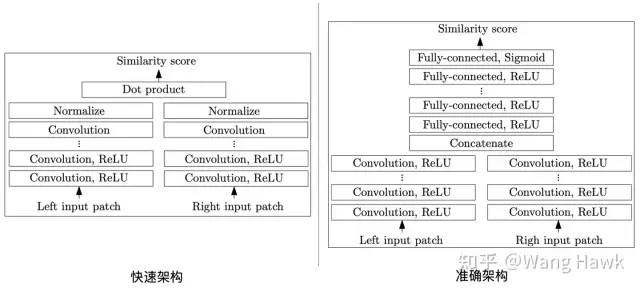
MC-CNN的两种架构 我们可以利用下图来描述它们的共同点，它们都是由左右两条分支组成了特征提取的网络，提取出来的特征图都会进入到决策模块，该模块负责计算出左右两个Patch对应的两个特征图之间的相似度，所以整个网络分为特征提取和分类决策这两部分。

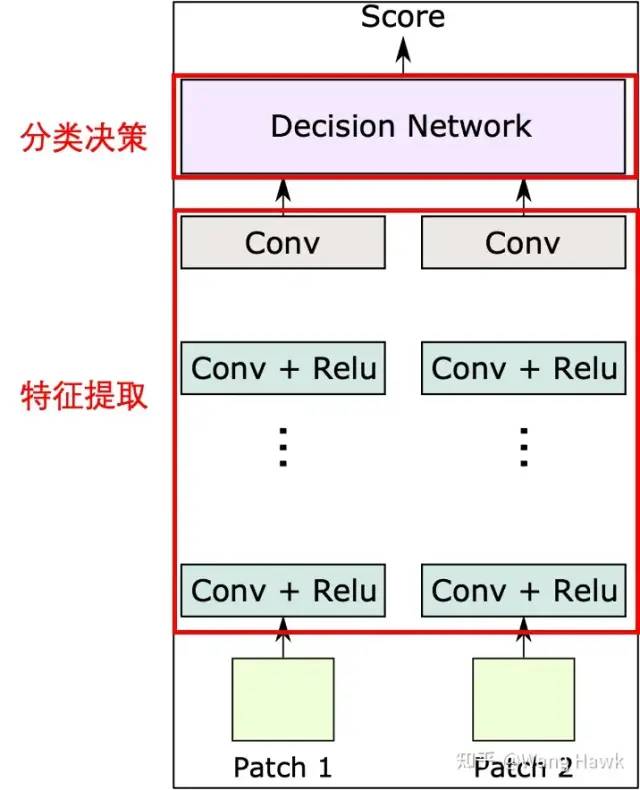
基本网络构成 它们的不同点是：

特征提取网络不同。除开层数等信息之外，fast结构还在特征提取网络的尾部添加了归一化层，用于对特征图进行归一化。

分类决策部分不同，fast结构中，特征图在每个分支中已经进行了归一化。所以分支决策部分直接是计算两个归一化的特征图的点积，及余弦相似度。而在accurate架构中，特征图首先在通道维度连接在一起，然后经过多个全连接层，再通过Sigmoid函数得到最后的相似度得分

这种架构可以快速判断左右两幅图中取出的两个Patch是否相似，结构也很简单，所以很多学者采用了这种架构，并进行了改进，我在下一节会谈到各种改进方向。

1.2 相似度计算

在特征提取之后，特征被送入上层模块进行相似度的计算。相似度计算是立体匹配算法的核心部分，可以分为两大类：手动相似度计算和决策网络。

1.2.1 手动相似度计算

手动相似度计算无需训练，它直接通过一些预先定义好的距离度量方法计算特征之间的相似性。常见的手动相似度计算方法包括L2距离、余弦距离、归一化的相关度或归一化内积等。这些方法的优势在于可以通过卷积操作实现，提高计算效率，并且无需训练。然而，它们可能无法充分适应不同的数据集特性，导致匹配精度受到限制。MC-CNN-fst算法就是采用的这种方式

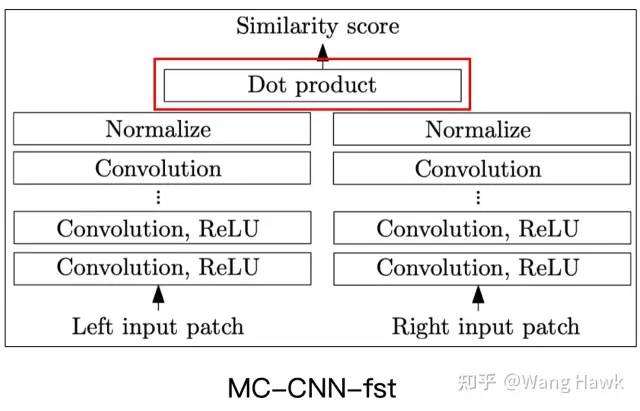
快速架构采用余弦相似度

1.2.2 采用神经网络计算相似度

与手动相似度计算相比，用于决策的神经网络需要训练，但可以提供更准确的相似度计算结果。决策网络可以采用1x1卷积、全卷积层实现，或通过卷积层与全连接层的组合实现。决策网络与特征提取模块联合训练，从而学习到更适应当前数据集的相似度计算方式， MC-CNN-acrt就是典型代表

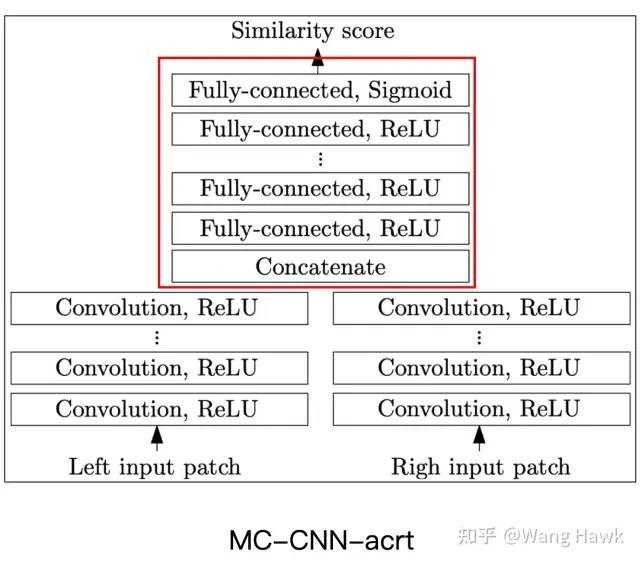
准确架构采用Sigmoid结果 全连接层实现的方法包括Han等人[4]的全连接层+SoftMax，Zagoruyko和Komodakis[5]的方法，以及Zbontar等人[3]提出的MC-CNN-acrt网络。在这些方法中，特征提取分支的特征图的结合方式有两种：一种是在通道层面连接[4][5][3]，另一种是通过类似Mean Pooling等方式连接[5]，这样可以处理任意多个Patch的相似度，而不用改变网络结构。

决策网络的优点是相似度计算结果更加适配当前的数据集，因此匹配精度更高，但相应地计算速度会更慢。因此，在实际应用中，需要根据具体问题和场景权衡决策网络与手动相似度计算方法的选择。

2. 网络的变种

在上面结构的基础上，很多学者研究了各种改进和提升的方法，这一节我们就来谈谈各种改进

2.1 引入Max-pooling操作处理大视差和大尺度Patch

回顾一下最简单的立体匹配代价计算公式：

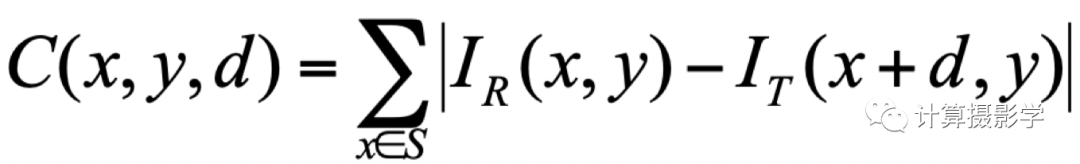
SAD代价计算公式 我们看到整个计算的时间复杂度是O(WHSD)，其中W/H是图像的长宽，S是支持窗的尺寸，D则是视差值的范围。所以支持窗越大，计算复杂度越高。对应到我们的深度学习架构中，特征图越大，计算复杂度越高。对应到我们深度学习的方法里面，则是特征图越大，计算复杂度越高，视差范围越大，计算复杂度越高。所以为了解决原始MC-CNN在处理大视差和大尺寸Patch时的效率问题，Zagoruyko和Komodakis[37]以及Han等人[4]在每层后面都添加了max-pooling和下采样操作。这样做的目的是使网络能够适应更大的Patch尺寸和视角变化。通过这种方式，增强的架构能够在保持较高匹配精度的同时提高处理速度，因为这样得到的特征图尺寸更小，如下图所示：

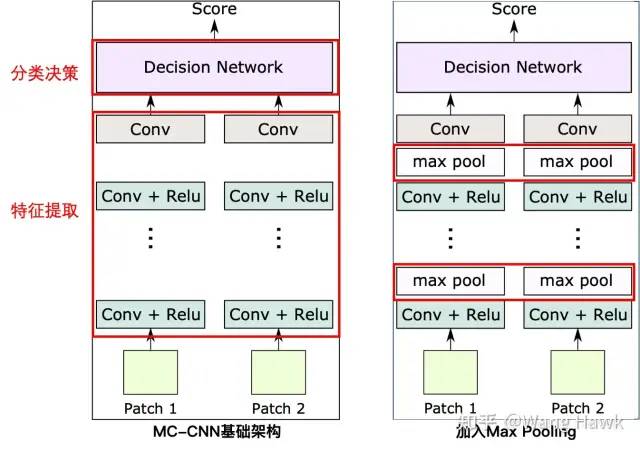
加入Max Pooling前后对比

2.2 引入SPP模块增强网络结构应对不同尺度输入时的灵活性

另一个重要的改进是在特征计算分支的末端加入了空间金字塔池化（SPP）模块。SPP模块可以输入任意尺寸的特征Patch，输出固定尺寸的特征图（如图2-c所示）。SPP的Pooling尺寸根据输入尺寸而改变，这样使得不同尺寸的输入可以得到相同尺寸的输出。这样当输入的Patch尺寸改变时，网络结构不用改变。这一点对于处理不同尺寸的图像数据具有重要意义，使得这个架构更具灵活性。

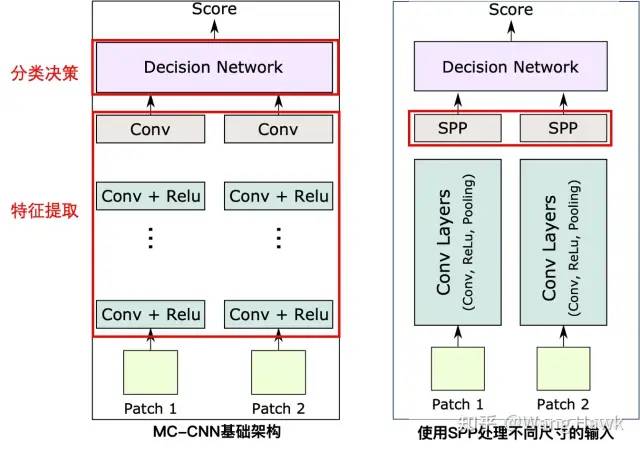
加入SPP前后对比

2.3 使用ResNet使得网络可以更深

这一点我想很多读者都不陌生，ResNet已经广泛应用在各种领域的神经网络里面了，所以尽管最初时，类似MC-CNN这样的算法还没有采用残差网络结构，后续的算法几乎都加入了这个结构。比如Shaked and Wolf [6]就使用了ResNet，构建了如下的网络结构，这里浅红色标注的部分就是典型的残差模块，这使得我们可以训练非常深的网络，从而捕捉到图像中更高层次的特征：

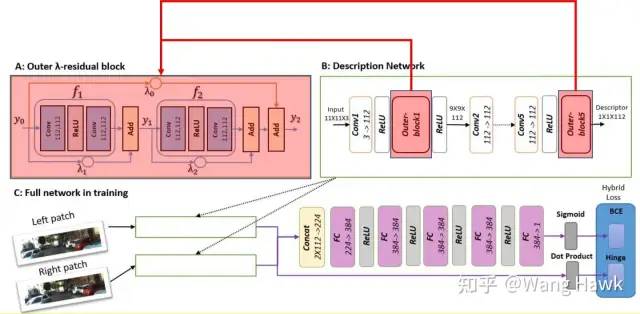
采用ResNet加深网络

2.4 使用空洞卷积或SPP得到更大的感受野

我在70. 三维重建5-立体匹配1，立体匹配算法总体理解中讲过，在重复纹理、无纹理区域我们是希望尽量采用大尺寸的支持窗来来提升信噪比和像素之间的区分度。

不同尺度的支持窗 对应到我们深度学习的算法中，则是我们在某些时候需要更大的感受野。扩大感受野的方法有多种，比如增大输入Patch的尺寸、或是使用更大的卷积核再配合带有更大步长的池化操作降低尺寸。前者会导致计算复杂度上升，后者则会导致特征图的分辨率降低使得细节丢失。所以就有了两种更好的方式

2.4.1 使用空洞卷积来提升感受野尺寸

第一种方法是使用空洞卷积——顾名思义，空洞卷积的卷积核是有空洞的，这样使得我们可以有更大的感受野，但是计算量却不改变，这种技巧后来被用到了很多领域。

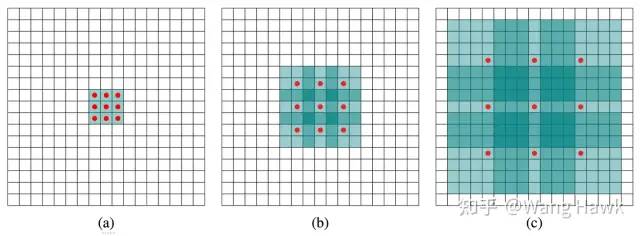
空洞卷积 下图是普通卷积（左）和空洞卷积（右）的对比：

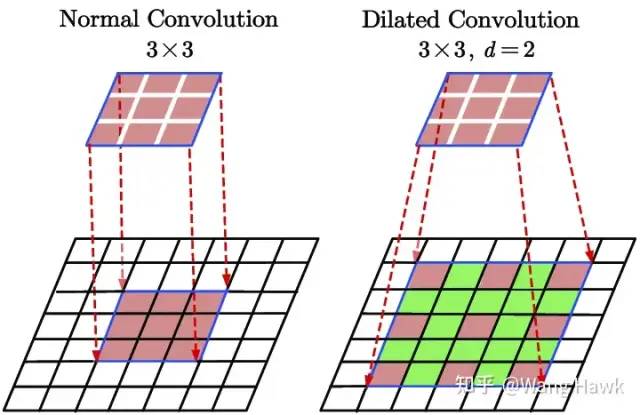
2.4.2 使用SPP来提升感受野尺寸

我们上面见过引入SPP模块可以使得网络可以灵活应对不同尺寸的输入，而其中一个重要的应用就是利用SPP模块来扩大感受野。比如Park et al. [11]提出了一种叫做FW-CNN的网络架构，其中引入了一个简称为4P的模块，即所谓Per-pixel Pyramid Pooling - 逐像素的金字塔池化操作。 我们之前讲过，如果采用更大的卷积核，加上更大步长的小尺寸的池化操作，可以扩大感受野——但这样会导致丢失原始特征图中的细节信息。如果换成更大尺寸的池化操作，但步长设置为1呢，这样当然也可以有更大的感受野——但同样也会丢失图像的细节。于是，这里的4P操作就对每个像素同时采用多种不同尺寸的池化窗口，并将输出连接以创建新的特征图。生成的特征图包含了从粗到细的尺度信息：

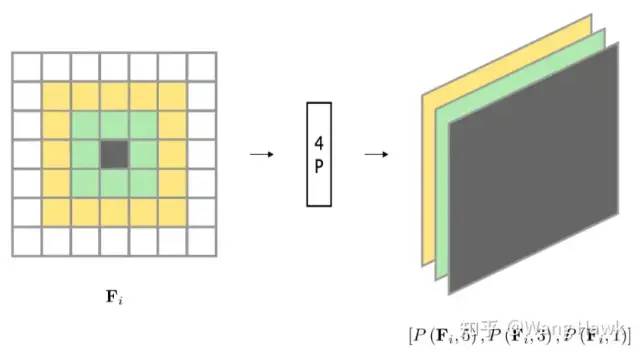
4P操作可以加入到网络的不同位置，在FW-CNN中，4P模块的位置如下所示：

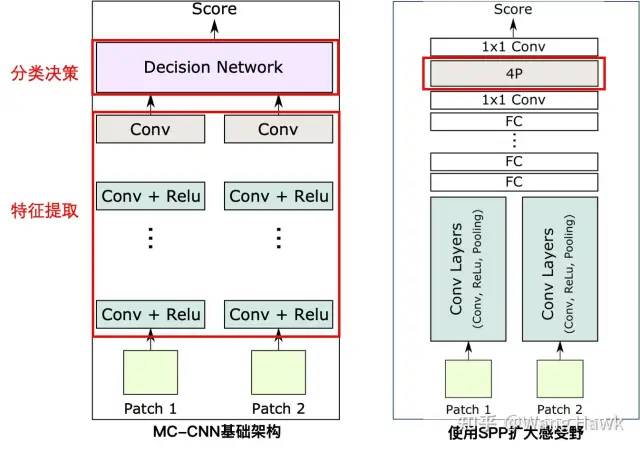
FW-CNN的这种方式虽然扩大了感受野，但是4P模块需要和全连接层一样，每个视差层级计算一次，所以计算量比较大。因此，Ye et al. [7]等提出了一种改进的方式，把SPP放到每个特征计算分支的末尾，并且采用多尺度的SPP，既降低了计算量，又能有较大的感受野。

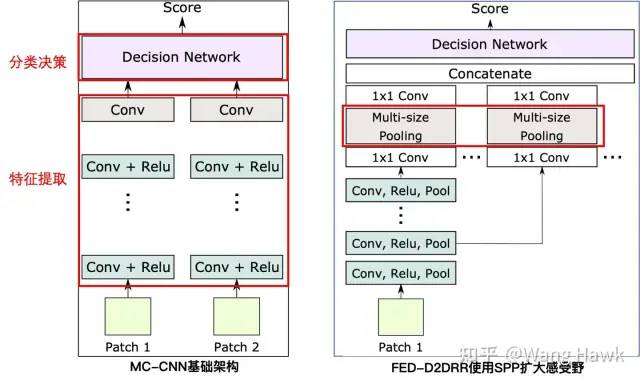
2.5 使用多尺度特征得到更好的结果 前面的方法都是采用一种尺寸的输入Patch，但在基础架构的基础上，还可以扩展到学习多尺度的Patch的特征，进一步提升效果，比如Zagoruyko和Komodakis[5]中提到了一种架构如下：

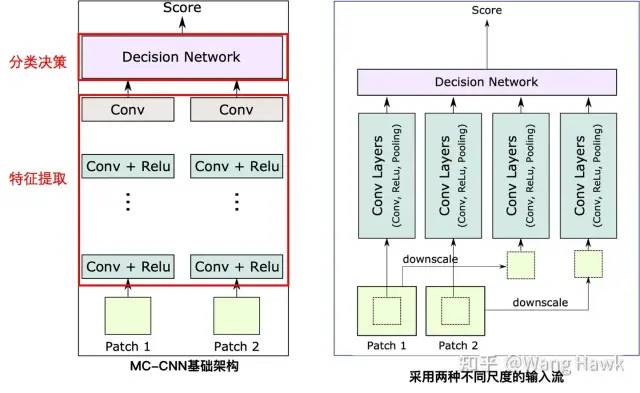
这里有两种输入，第一种是从输入的Patch中心裁剪32x32的区域送入网络，第二种是将输入的64x64的Patch缩小为32x32送入网络。因此前者比后者的解析力更高。这样网络在单次前向推理后就可以提取到不同尺度和解析力的特征，效果也就更好，效率也较高。Chen et al. [8]等提出了一种类似的结构，只不过两组流各自做各自的特征提取和分类决策，决策的结果再通过投票整合到一起，作为最后的输出。

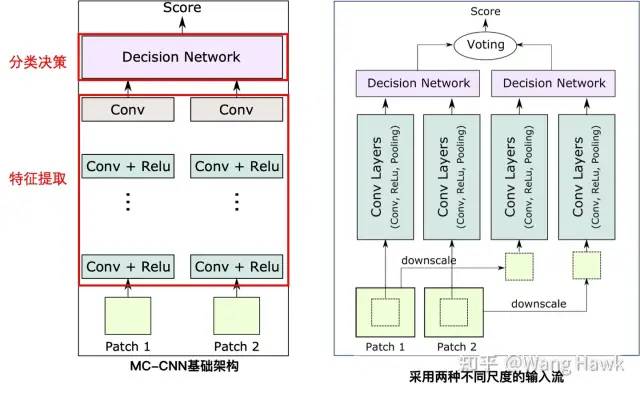
2.6 改变网络结构，得到更高的效率

2.6.1 一次性计算所有视差层级的代价

前面我们讲的方法在分类决策时，每个像素需要n_d次通过决策模块来计算代价，其中nd是视差层次的数量。如果我们的决策模块采用的是相关计算（类似内积计算），那么可以利用到相关性天然的高度并行性来大大减少前向传播次数。例如，Luo等人[9] 就提出了下面这样的结构，这里左图的Patch尺寸不变，但右图会采用更大尺寸的Patch，这样一次性最大可以把所有可能得右图Patch的特征全部提取出来，然后通过并行的相关性计算一次性把该像素所有可能的代价计算出来。在这个网络中，左图的特征是64维的，而右图提到的特征则是nd x 64维的。

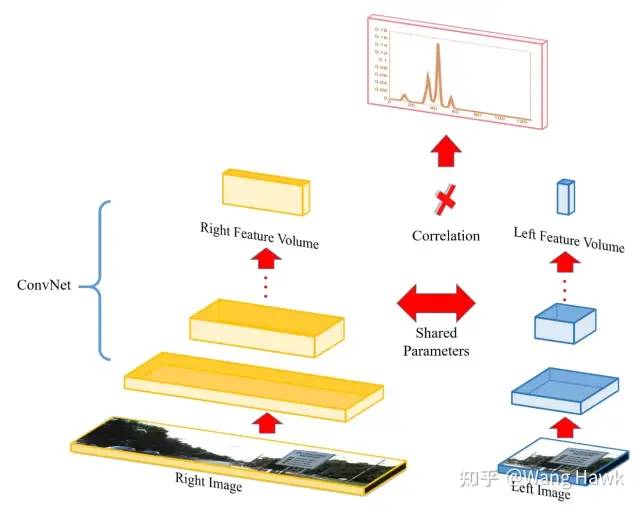
并行相关度计算提升效率

2.6.2 一次性提取特征

我们之前展示的结构的输入都是两个Patch，而非整个图像。在Zagoruyko和Komodakis[5]中提到，实际上可以通过输入两个图像，一次性提取左右两个视图的特征图，不需要逐Patch的计算，也不需要每个视差层级计算一次

2.6.3 对整幅图计算代价，而非逐Patch计算

另外，在Zagoruyko和Komodakis[5]还提到，可以通过将决策网络中的全连接层改为1x1卷积操作，这样就可以对整幅图计算代价，而不是对Patch计算，当然每个视差层级还是需要计算一次。 以上两个方法在我上一篇文章种已经讲过了，下面是我当时给的伪代码

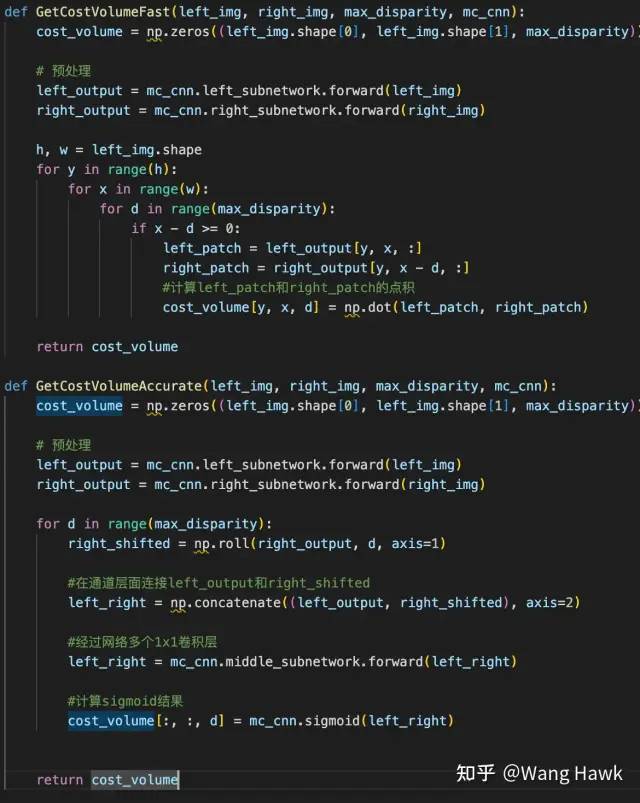
加速推理的伪代码

2.7 整合特征提取和决策模块，得到更好的效果

在Zagoruyko and Komodakis [5]中还提到了一种特别的结构，输入的两个Patch从一开始就整合成多通道的图像送入网络。于是网络没有专门分开的特征提取模块，而是将特征提取与决策整合到一起，如下所示。这种结构训练比较简单，不过在推理时效率低，因为每个像素需要推理nd次：

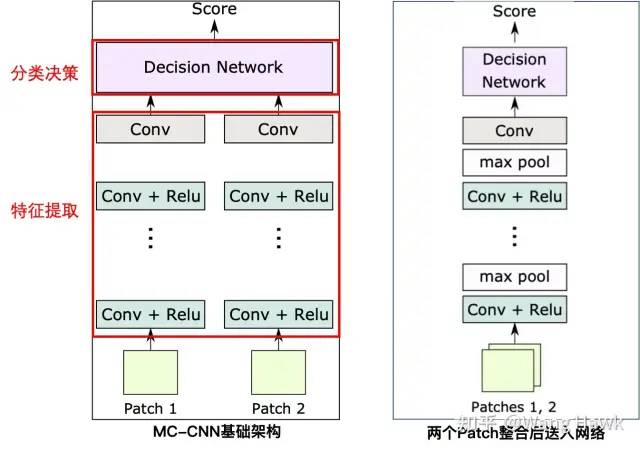
通道维度上连接图像再送入网络 这种将多个输入直接在通道维度上连接再送入网络的方式很有用，我们之后还会看到类似的用法。这一节我们看到了多种网络结构的变种，而下一节我来介绍一下各类网络的训练策略。

3. 网络训练策略

我们之前看到的特征提取网络和代价决策网络都需要训练，而训练的策略则分为强监督型和弱监督型两类。我重点介绍一下强监督型训练，然后捎带提一下弱监督或自监督的训练策略

3.1 强监督型训练

这里面又分为两种形式。 第一种的训练样本的基本单元是一对patch，它们要么是匹配的正样本，要么是不匹配的负样本。网络要学习的是这一对patch间的匹配程度。那么如果输入的是正样本对，理想的匹配程度为1，如果输入的是负样本对，那么理想的匹配程度为0。通过某些损失函数的迭代约束，网络会调整自身权重，使得最终能够甄别出输入patch对之间是匹配的还是不匹配的。

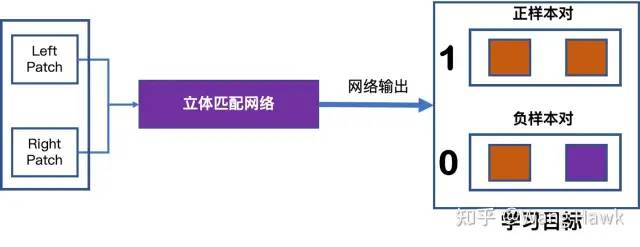
输入一对Patch进行训练 第二种的训练样本的基本单元是两对Patch，其中一对Patch是匹配的，其中右视图的Patch来自于与左视图对应的右极线上。另外一对Patch则是不匹配的。此时网络优化的目标是尽量放大这两对Patch的匹配值之间的差异。正样本对的相似度计算结果应该比负样本对的相似度计算结果大得多。

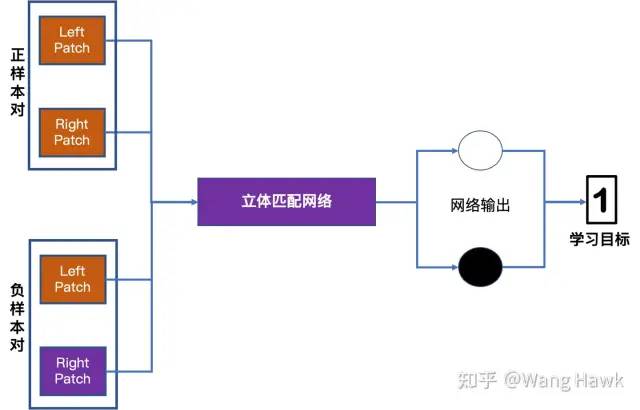
输入两对Patch进行训练 强监督训练的损失函数用于衡量网络输出和学习目标之间的差异，主要有三类损失函数

L1距离

Hinge损失函数

交叉熵损失函数

3.2 弱监督型训练

为了减少对标注数据的需求，人们提出了弱监督训练方式，这通常是通过引入一些先验信息约束网络的学习过程来实现的，Tulyakov等人[10]就利用多实例学习（MIL）结合立体约束和关于场景的粗略信息，来训练立体匹配网络，而这些数据集并没有可用的真实标签。 跟传统的监督技术不同，弱监督训练并不需要成对的匹配和不匹配图像块。实际上，训练集是由N个三元组组成的。每个三元组包括：（1）从参考图像上的水平线上提取的W个参考块；（2）从右图像对应的水平线上提取的W个Patch，作者成为正Patch，它们跟W个参考块有可能是匹配的；（3）从右图像上另一个水平线上提取的W个负Patch，即与参考块绝对不匹配的块。这样一来，我们就可以直接从立体图像对中自动生成训练集，不需要手动进行标注了。 在训练网络时，研究人员使用了五个约束条件来引导学习过程：

对极约束：这个约束告诉我们，在左右图像中的匹配点必须位于相应的水平线上。

视差范围约束：它告诉我们每个像素的视差值在一个已知的范围内。

唯一性约束：对于每个参考像素，只能有一个唯一的匹配像素。

连续性（平滑性）约束：表示物体表面的视差变化通常是平滑的，除非在物体边界附近发生突变。

排序约束：指的是在左图像上的参考点之间的顺序应该与在右图像上的匹配点之间的顺序一致。

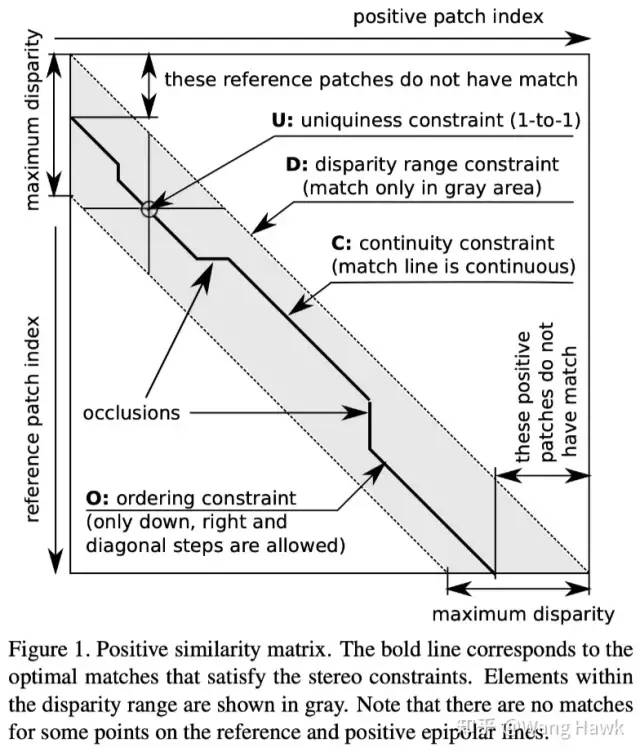
根据这些约束条件，研究人员定义了三个损失函数来引导网络学习。其中，多实例学习（MIL）损失使用了对极约束和视差范围约束。收缩损失在MIL损失的基础上增加了唯一性约束，使得匹配点更加准确。收缩-DP损失则结合了所有约束条件，并利用动态规划来寻找最佳匹配。 通过这种方法，网络能够根据这些约束条件进行学习，从而在没有充分标注的数据集上实现立体匹配。

4. 思考和小结

在本文中，我们介绍了深度学习立体匹配方法的基础网络架构和常见的网络变种，以及训练策略。我们看到，在不同的应用场景下，立体匹配问题需要不同的解决方案。为了应对这些挑战，研究者们提出了各种改进和优化方法，从网络结构到训练策略都进行了探索。其中我们列出了网络结构的各种变种

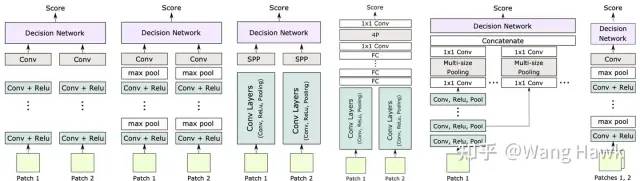
尽管深度学习立体匹配方法已经取得了显著的进展，但仍然存在一些问题需要进一步研究和解决。例如，对于大视差和大尺度Patch的处理、不同尺度输入的灵活性、更高的效率等方面还有改进的空间。此外，如何将深度学习方法应用于实际应用中，也是需要进一步探索和研究的问题。 我们目前看到的方法，都是类似MC-CNN这样遵循了传统立体匹配架构的方法。我会在下一篇文章开始介绍端到端的立体匹配算法，它们遵循完全不同的策略和逻辑，一定会给你带来不一样的感受！ 下面是你现在的位置，喜欢今天的文章就点个赞，持续关注我吧！

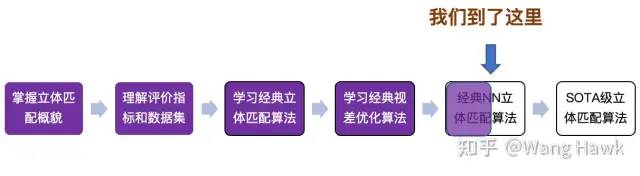
学习进度地图

审核编辑 ：李倩