PCB电源电容退耦半径讲解

理解去耦半径最好的办法就是考察噪声源和电容补偿电流之间的相位关系。当芯片对电流的需求发生变化时，会在电源平面的一个很小的局部区域内产生电压扰动，电容要补偿这一电流(或电压)，就必须先感知到这个电压扰动。信号在介质中传播需要一定的时间，因此从发生局部电压扰动到电容感知到这一扰动之间有一个时间延迟。同样，电容的补偿电流到达扰动区也需要一个延迟。因此必然造成噪声源和电容补偿电流之间的相位上的不一致。

特定的电容，对与它自谐振频率相同的噪声补偿效果最好，我们以这个频率来衡量这种相位关系。 设自谐振频率为 f，对应波长为λ，补偿电流表达式可写为：

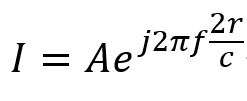
其中，A 是电流幅度，r 为需要补偿的区域到电容的距离，C为信号传播速度。 当扰动区到电容的距离达到λ/4(相位差90°)时，补偿电流到达噪声源的相位为180°(来回的距离是λ/2)，即完全反相(最差的情况，去耦电容失去作用)。 此时补偿电流不再起作用，补偿的能量无法及时送达。 为了能有效传递补偿能量，应使噪声源和补偿电流的相位差尽可能的小，最好是同相位的。 距离越近，相位差越小，补偿能量传递越多，如果距离为0，则补偿能量百分之百传递到扰动区。 这就要求噪声源距离电容尽可能的近，要远小于λ/4。 实际应用中，这一距离最好控制在λ/40-λ/50(甚至更小λ/60)，这是经验数据。

举例说明：

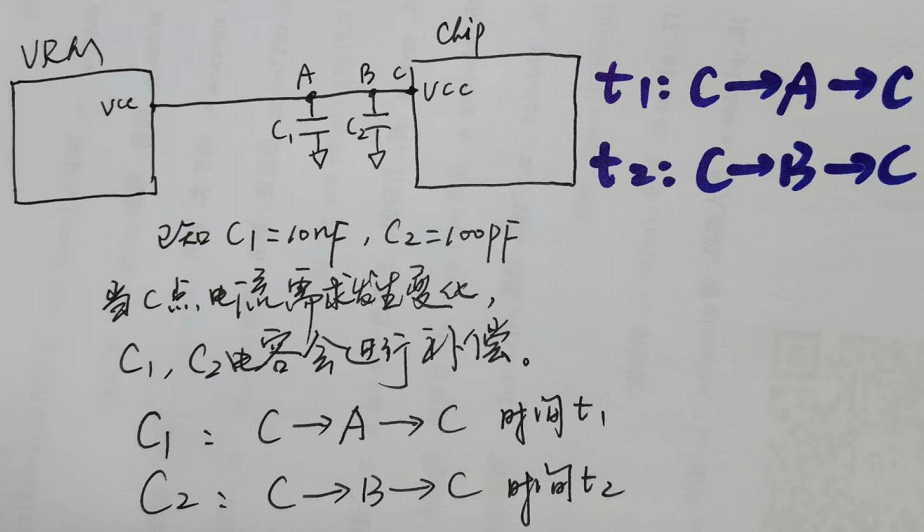
首先找到电容C1,C2对应自谐振频率，一般计算方式：

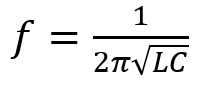
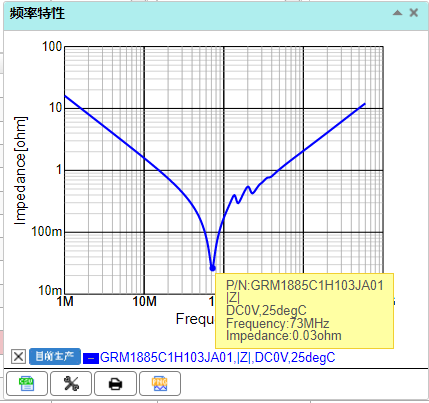
如果用村田的MLCC电容，可直接使用Simsurfing辅助工具，结果更精准。

C2： GRM0335C1E101FA01 f2=940MHz

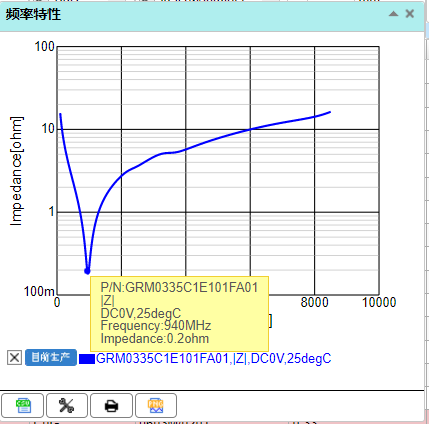
C1：GRM1885C1H103JA01 f1=73MHz

信号在PCB上传播速度：

v（PCB）=166ps/英寸=6英寸/秒

C1波长：

λ1=V/F1=6英寸/纳秒*13.7ns=82.2英寸

C2波长：

λ2=V/F2=6英寸/纳秒*1ns =6英寸

C1耦合半径:

R1=λ1/50=82.2英寸/50=1.64英寸=4.17厘米

C2耦合半径:

R2=λ2/50=6英寸/50=0.12英寸=0.3厘米