

如何利用CUDA实现一个2D卷积算子
人工智能
描述
本篇文章主要介绍如何利用CUDA实现一个2D卷积算子,实现过程较为简单,最终的实现效果可以在较小的尺寸下取得比cudnn快较大的性能。实测在以下参数配置下可以达到平均1.2倍cudnn的性能。
前言
CUDA介绍(from chatGPT)

现在深度学习大行其道,作为深度学习的基础软件设施,学习cuda也是很有意义的。本篇文章主要介绍如何利用CUDA实现一个2D卷积算子,实现过程较为简单,最终的实现效果可以在较小的尺寸下取得比cudnn快较大的性能。实测在以下参数配置下可以达到平均1.2倍cudnn的性能(娱乐结果,还与cudnn配置有关,更小更快)。
TIPS: 跳过cudnn初始化的时间,99轮平均时间
const int inC = 6; const int inH = 768; const int inW = 512; const int kernelH = 6; const int kernelW = 6; const int outC = 6; const int outH = inH - kernelH + 1; const int outW = inW - kernelW + 1
1 卷积操作通俗介绍
1.1 数据布局(data layout)
卷积操作主要针对图像进行运算,我们常见的RGB即为三通道的二维图像,那么就可以通过一个一维数组存储所有的数据,再按照不同的布局去索引对应的数据,现在主要使用nchw和nhwc两种数据布局,其中
n - batch size 也可以理解为"图像"数量
c - channel num 即我们说的通道数量
h - height 图像高度,每个通道的高度宽度是一致的
w - width 图像宽度
那么显然nchw就是逐个通道的读取图像,nhwc即对所有通道的同样位置读取数据后,再切换到下一个为止
一个是优先通道读取,一个是优先位置读取
还有一种CHWN布局,感觉比较奇怪,并未过多了解
详细的可以参考英伟达官方文档Developer Guide : NVIDIA Deep Learning cuDNN Documentation (https://docs.nvidia.com/deeplearning/cudnn/developer-guide/index.html)
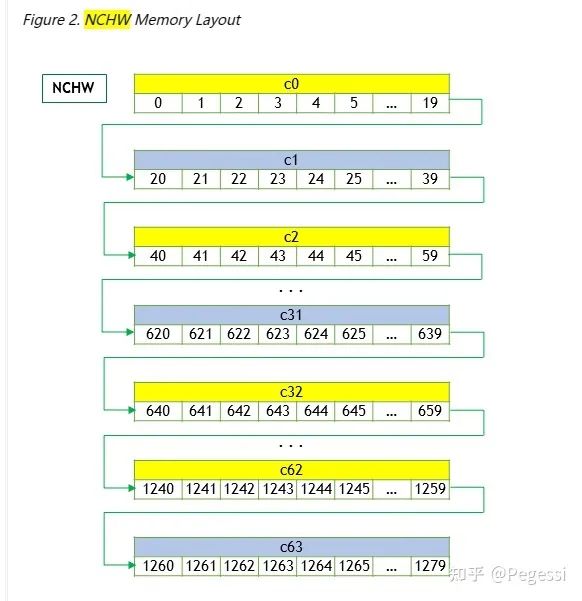
nchw layout
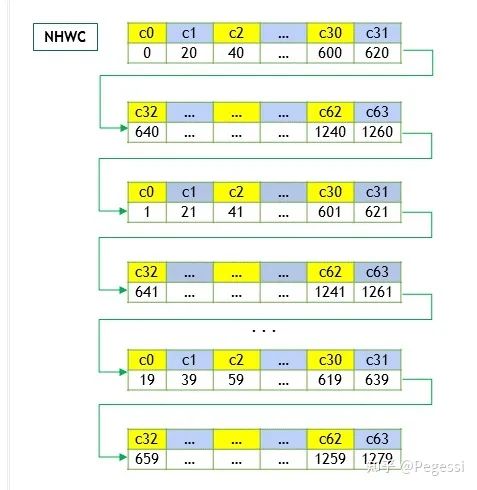
nhwc layout
本文是按照nchw数据格式来进行算子的实现的。
1.2 直接卷积
相信大家都或多或少听过卷积,可以通过gpt的回答来直观地认识卷积操作

最基本的直接卷积操作是十分简单的,你可以想象一个滑动的矩阵窗口在原矩阵上移动,对应位置进行点积,得到结果后求和放到目标矩阵上,可以用以下图像直观地理解这一过程,向老师称为对对碰:)
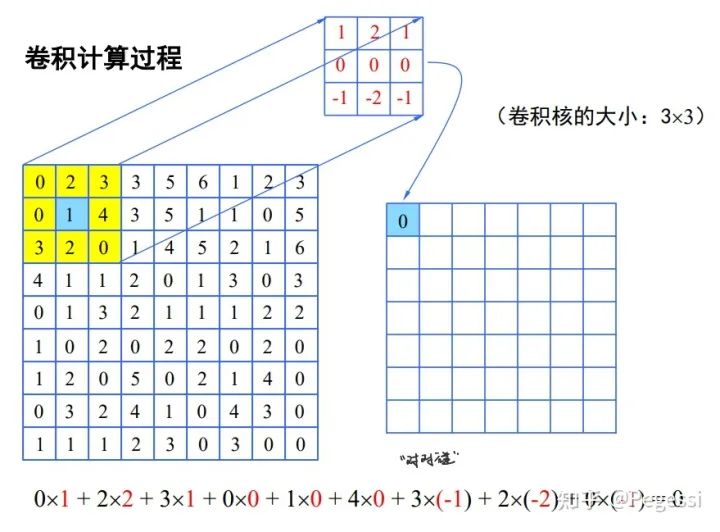
图源:国科大模式识别课程
你会注意到上述过程中怎么没有什么channel的参与,只有一个矩阵
多输入通道的情况下,就是对每个通道的相同位置分别与卷积核进行对对碰,结果累加作为输出矩阵值;
多输入多输出通道,即对每个输出通道都进行上述操作
对于通道的理解建议参考[@双手插袋]的文章CNN卷积核与通道讲解 (https://zhuanlan.zhihu.com/p/251068800)
那么我们需要知道的是直接卷积操作其实就是原矩阵与卷积核间的对对碰,产生所谓的特征图feature map,十分的简单,这也方便我们对其进行并行任务划分
注意到上述文章中并没有提到padding和stride,本篇文章并没有针对padding和stride的实现
padding
padding是作为对图像的填充,可以发现上面的特征图尺寸缩小了一圈,是因为直接卷积势必会造成这一结果
通过padding可以加强图像边缘特征,避免边缘特征被忽略
stride
stride可以简单的理解为跨步,即上面的小窗口在矩阵上滑动的步长,默认为1
即上述图像中下一次卷积的中心应该是4为中心的3*3子矩阵
如果你设置为2,那么下一次是3为中心的3*3子矩阵了
1.3 其他卷积计算方法
除去直接卷积,也有一些其他方法进行卷积,感兴趣的读者可以自行了解,仅举以下几例参考
Img2col
即把图像展开为一个行向量组,卷积核/滤波器(kernel/filter)展开为一列或多列向量,转化为矩阵乘去计算卷积结果
FFT method
利用傅里叶变换的频域变换去做卷积,这样做的优势是计算量会小很多
Winograd Algorithm
也是一种将图像变换到另外一个空间再去做运算再做变换得到结果,会减少很多乘法运算
2 整体实现思路
2.1 block与thread划分
首先我们需要考虑如何对代表图像的多通道矩阵来进行block与thread的划分,这一部分是有说法的
不同的切分方式会让block在SM上的流转效率有很大的差别
本文仅提供一个十分草率的切分,我们都清楚目前在英伟达的GPU上,任务的调度最小单元是warp
一个warp以32个线程为一组,故通过8*4的block来进行矩阵的切分,每个block里共32个位置
这样可以保证每个block上到SM时不用去与其他的block拼接线程,产生额外开销
注意我这里用的是位置,并不是元素,32个线程,每个线程去负责一个位置的计算
以16*20的矩阵为例,对其进行划分的结果如下图所示,(x,y)是笛卡尔坐标系,与行主序不同
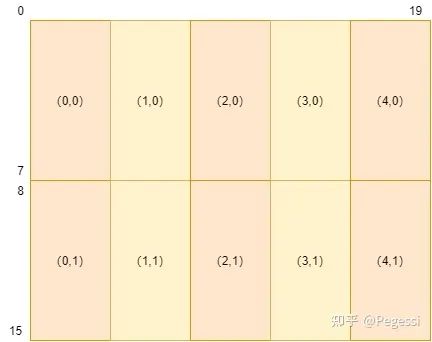
2.2 数据转移
关于位置和规模(size)
那么为什么说一个block有32个位置,而不是32个元素呢,首先注意到卷积操作虽然遍历到了原矩阵的所有元素
但是你按中心点的位序去数的话(以卷积核3*3为例),结果应该是这个样子
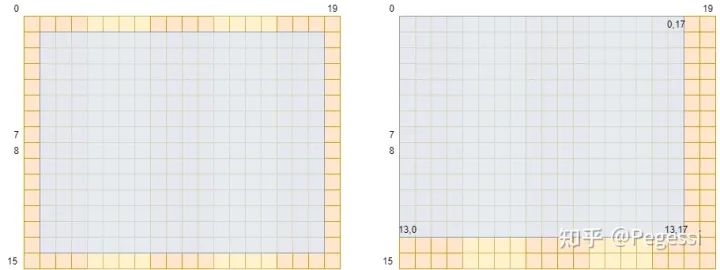
注意这里仅示意卷积中心点范围,请与后文作区分
按3*3矩阵的中心来看,中心正好是去掉外面一圈的位置,按照左上角元素来看,恰好应该是(左上角,右下角)
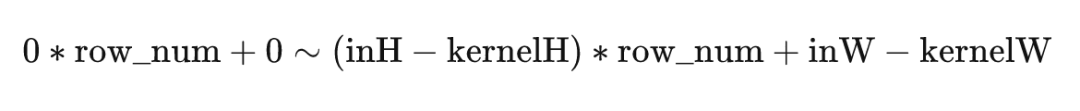
这样一个区间,参数解释如下
row_num 原矩阵中一行元素的数目
inH inW 原矩阵的H W
kernelH kernelW 卷积核的H W
outH outW 输出矩阵的H W
当然你也可以用中心点而不是左上角的元素作为窗口的标识来设计算法
恰巧你上面算出来的这个范围也正是你得到的feature map的下标范围
我们也可以得到输出矩阵的规模为
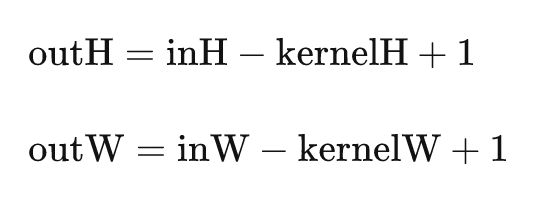
请注意大小和位置下标的区别,一个从1开始数一个从0开始数
一个block的数据转移
确定了整体的尺寸,那么我们来看一个block需要的数据尺寸是多少呢
显然你可以发现,对于输出矩阵进行block划分是更合理的,这样可以保证一个block
32个位置恰好对应输出矩阵的32个位置,而不用过多的去考虑输出矩阵的排布
那么对于上述提到的划分,可以通过下图来直观感受block划分在原矩阵的效果
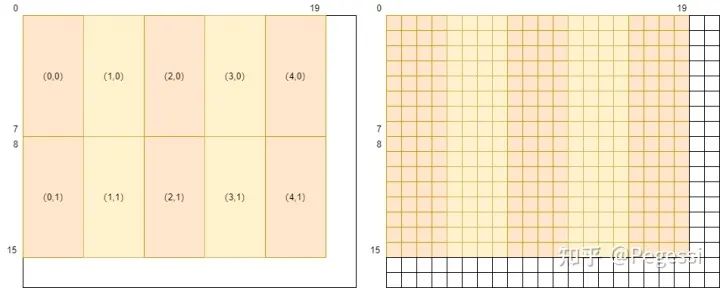
22*18的in产生20*16的out
那么一个block用到的元素范围应该是哪些呢,我们要做的是卷积操作,每个中心点应该有对应卷积核大小的矩阵参与运算,那么以(0,0)和(4,1)的block为例,给出他们的涉及原矩阵范围如下图所示
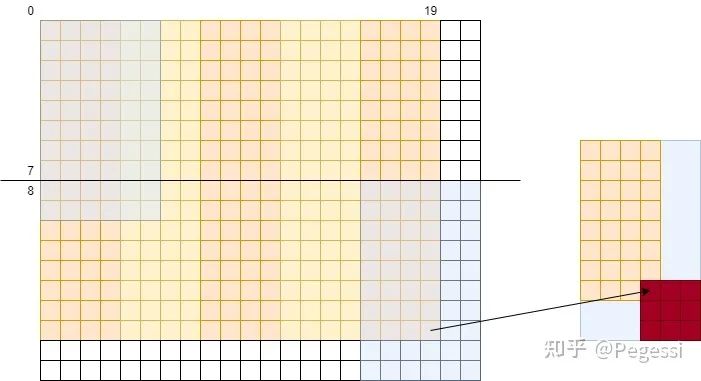
蓝色为一个block需要用到的原矩阵元素
那么我们可以确定一个block,8×4的情况下需要读取10×6的原矩阵的元素,也是+kernelH-1来确定的
那么对应输出矩阵就是一个萝卜一个坑了,不需要额外考虑
这样就确定了一个block需要从GMEM到SMEM的元素范围
至于怎么转移,我们在代码实现中讲述,当然你可以单独指定某几个进程去完成所有的转移任务
2.3 计算逻辑
不考虑channel
不考虑channel的情况下,即单输入通道单输出通道单卷积核这样最简单的情况
我们只需要做三件事
① 将block对应的数据转移到SMEM中
② 利用线程的tid去计算对应输出矩阵位置的结果
③ 将结果写回输出矩阵
只考虑inC
这种情况下我们要做的额外的事儿就多一点
加一层循环,让每个线程计算多个in channel的数据,并累加起来作为结果
需要用到一个寄存器来存储这个中间结果
考虑inC与outC
其实要做的事情也就比上面多一点,就是开大点空间
让线程去存储多个outC的中间结果,分别累加
最后写回的时候也分别写回即可
3 详细实现过程
3.1 整体实现思路
主要从自己的角度出发去还原怎样一步步构造出这样一个初级的算法
首先实现一个最简单的版本,CPU串行版本,并保证CPU串行版本可以获取正确的结果
此后再在其基础上进行并行化的改造,而直接卷积运算的过程其实相对是比较简单的
我们在不考虑padding与stride的情况下,是可以不借助任何参考资料来直接完成第一版代码的
3.1.1 CPU串行版本的卷积算子
#define element_type float
#define OFFSET(row, col, ld) ((row) * (ld) + (col))
/*
@brief: 串行卷积实现 CPU代码 NCHW
@param in inC inH inW: 输入矩阵(数组) channel height width
@param out outC outH outW: 输出矩阵 channel height width
@param kernel kernelH kernelW: 卷积核 height width
*/
void serial_convolution(element_type *in, element_type *out, element_type *kernel, int batch_size,
int inC, int inH, int inW,
int outC, int outH, int outW,
int kernelH, int kernelW)
{
float val;
int out_pos, in_pos, kernel_pos;
for (int oc = 0; oc < outC; oc++) // 每个输出通道
{
// 对一个位置的操作 用当前输入channel卷积去对相应的输出channel
// 保证每个outChannel都是多inChannel累积的结果
for (int i = 0; i < outH; i++)
{
for (int j = 0; j < outW; j++)
{
val = 0; // 避免累积和需要多次读取写入
out_pos = oc * outH * outW + OFFSET(i, j, outW);
for (int ic = 0; ic < inC; ic++) // 对每个输入通道
{
for (int ii = 0; ii < kernelH; ii++)
{
for (int jj = 0; jj < kernelW; jj++)
{
in_pos = ic * inH * inW + OFFSET(i + ii, j + jj, inW);
kernel_pos = oc * kernelH * kernelW + OFFSET(ii, jj, kernelW);
val += in[in_pos] * kernel[kernel_pos];
}
}
}
out[out_pos] = val; // 与cudnn计算结果为相反数
}
}
}
}
这是我最终完成的CPU串行版本代码,可以发现套了足足有5层循环
在我们传统观念中,这可是 O(n5)O(n^5)O(n^5) 的最笨算法了
不过没有关系,我们关注的并不是他的性能,cuda上也不会去跑这一版代码
我们需要关注的是怎么样能得到正确的结果,且如何设计循环的嵌套关系来使用尽量少的访存次数
使用尽量多的本地中间结果,这样可以尽可能地减少我们的算法在访存方面的消耗
要明白GPU上的线程如果去读GMEM上的数据需要几百个时钟周期,读SMEM需要几十个时钟周期
读取SM上的寄存器需要的时钟周期会更少!
因此我们需要竭力优化的一部分是如何减少访存,多用本地存储来代替
另一方面这也是因为计算本身是十分简单的点积,不太可能去做出更大的优化
3.1.2 循环顺序设计
逐层去观察循环的嵌套顺序,发现是
outC-->H-->W--->inC-->kernelH-->kernelW
这样的计算顺序不一定是最优化的,笔者也没有进行详细的计算论证,但是这样的计算顺序是出于以下角度考虑
① 多通道卷积结果的维度/通道数/feature map数就是我们的outC,是我们最终要写回的out矩阵的维度,将其放在最外层循环,作用是:
一次循环内完成这个out channel中的所有计算,再接着进行下一个outC的计算
由于out数据是在一维数组中存储,且为nchw格式,那么不同outC中的数据跨度其实是很大的,连续的完成一个outC的内容可以更好的利用局部性原理
个人理解逐个outC的计算是很是一种比较直观和自然(方便想象与理解)的角度
串行过程中我们可以使用尽量少的中间变量去维护中间结果,如果你先遍历inC后遍历outC的话,其实你是需要维护outC个中间变量的
这样的顺序也是在后面做并行化改造过程中逐渐发现的一个较为合理的顺序,我们可以在后文中更加直观的感受到这样设计的优势
② 出于nchw布局的涉及,H W的顺序是基本固定的,当然你也可以先W后H,不过一般是行主序存储.. 还是先H比较快一些
③ inC为何出现在H W之后?请回顾多通道卷积的过程,一个feature map的值是由多个inC与kernel分别点击累加形成的,如果你将inC放置在H W之前的话,在下方的代码中,你是不是就需要设置height×width个中间变量来存储这里的val值呢?
in_pos = ic * inH * inW + OFFSET(i + ii, j + jj, inW); kernel_pos = oc * kernelH * kernelW + OFFSET(ii, jj, kernelW); val += in[in_pos] * kernel[kernel_pos];
将inC放置在H W之后,是相当于在一个outC上进行计算,对不同inC同样的位置分别计算得到了val的准确值,最终写回,这样在串行的版本中,我们只需要一个float即可存储好中间结果来避免空间的浪费!
TIPS:注意上方对于下标的计算,我们以两个位序举例说明
in_pos = ic * inH * inW + OFFSET(i + ii, j + jj, inW);
nchw的数据布局格式下,这里是默认n为1的,注意本文所有的实现都是建立在n假设为1的情况,其实n为更大值也不是很有意义,这样的布局下,下一张图像在计算意义上是没有任何差别的,无非是你将数据的起始地址跳过一大部分,切到下一张图像
说回这个式子,其中ic为in channel,inH inW分别是输入矩阵的高度与宽度,后面宏定义的OFFSET其实就是简略写法,你也可以写成(i+ii)*inW + j + jj
in_pos的含义是在当前循环变量下输入矩阵的位置
同理,out_pos的计算是一样的
out_pos = oc * outH * outW + OFFSET(i, j, outW);
ii和jj是相对于卷积核的相对位置循环变量,输出位置是用不到他们的
进行并行化改造
其实当你把串行版本设计明白后,你对于并行化改造的想法也差不多有个七七八八了
主要是出于以下三个角度去设计并优化的
① 尽量减少访存次数(当然不是不访问),尤其是减少访问GMEM的次数,善用SMEM与register
(对于GMEM SMEM和register等访存层次相关知识不熟的读者可以去了解一下CUDA的存储层次)
② 此外要划分明确各个线程要负责的任务区域和他的行为应达到的效果,做好下标计算
③ 计算行为是很快的,我们要尽可能去掩盖访存延迟,让线程去火力全开计算(预取prefetch)
下面的章节都是在并行化改造过程中的一些细节,代码其实是一版版写出来的,这里是对最终版本进行说明
(所谓的一版版就是划分出不同块,分别测试是否与预期一致,再去完成下面的块)
3.2 线程任务均分
这部分其实是源于 @有了琦琦的棍子 在GMEM讲解中的数据转移部分,基本算是照抄了
十分感谢前辈,不过还不知道这种方法的确切名字,目前暂时称为均分,其实思想是很朴素的
我们的block设计的是8*4的大小,对应32个线程,但是涉及到in矩阵的数据可不只是32个元素,那么
我们需要尽可能地平均分配任务给线程,保证每个线程承担差不多的任务量来达到更好的平均性能
差不多是因为,不太可能都是整除的情况
这部分主要通过图示讲解,自己设计的过程中大多是通过纸笔演算确定下标的
首先确定一些变量,注意CUDA的笛卡尔坐标系和笔者的行号row和列号col的区别
int block_row = blockIdx.y; int block_col = blockIdx.x; int thread_row = threadIdx.y, thread_col = threadIdx.x; int tid = thread_row * threadW + thread_col;
由于要重复使用inC内的数据,我们肯定是要开一个SMEM去存储这部分数据的,那么就有一个GMEM->SMEM的数据转移过程,以8×4的block和3×3的kernel为例,我们可以得到如下的景象
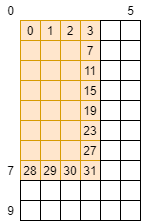
其中橙色部分是我们的block,一个tid(thread id)是一个线程,也是block中的一个位置,也是outC中的一个位置
那么白色部分就是我们在block范围之外但会用到的数据,这部分数据可以看到像两条网格
那么我们怎么把这些数据从GMEM转移到SMEM呢,首先我们考虑(以下部分为自己笨拙的思考过程)
方案① 边缘线程负责白色区域
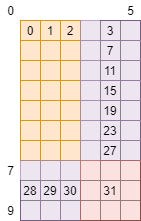 橙色为仅负责自己的位置,紫色负责3个位置,红色负责9个
橙色为仅负责自己的位置,紫色负责3个位置,红色负责9个
看起来是不是好像也还行,只要我们通过thread_row和thread_col判断一下当前进程是否在边缘
对这些进程进行单独的编码就可以了,不过在写代码前可以先算一笔账
这个网格共有10×6=60个元素,我们有32个线程,那么最好的情况下,是每个线程负责
60/32=1.875个元素,也就是花费1.875个单位时间(这里的单位时间是抽象概念,假定为每个线程处理每个元素的时间)
那么可以看一下这种划分方式下,每个线程平均负责的元素为
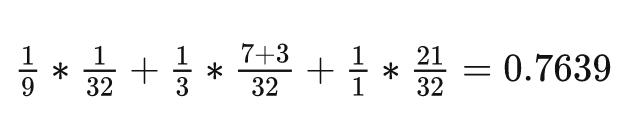
后面的项是权重,前面的项如 说明这个线程处理9个线程,那么花费的时间应当是9倍,所以性能应当是九分之一(相当于只处理一个元素的线程),且线程是warp调度的,32个线程里面有这么一个拖后腿分子,想必并行情况下整体花费时间是取决于这个31号线程的
这个方案的效率是理想情况的一半都不到,说明这种方案是不太可行的,写出来效果也不一定好呢,换!
方案② 平均划分
其实笔者也想过一些其他奇怪的方法,但是感觉平均思想似乎是最佳的,那么何不一步到胃呢?
我们先来定义一些变量,后面再来逐步解释
// 分块边界 boundary是限制正常范围 edge是需要补的范围
int row_boundary = outH / BLOCK_HEIGHT - 1,
col_boundary = outW / BLOCK_WIDTH - 1;
int row_edge = outH % BLOCK_HEIGHT, col_edge = outW % BLOCK_WIDTH;
···
int single_trans_ele_num = 4; // 线程一次转移的数据数
int cur_in_block_height = BLOCK_HEIGHT + KERNEL_HEIGHT - 1, // 读入in的block height
cur_in_block_width = BLOCK_WIDTH + KERNEL_WIDTH - 1, // 读入in的block width
in_tile_thread_per_row, // 以tile为单位转移数据,一行需要的thread数
in_tile_row_start, // tile的行起始位置
in_tile_col, // tile的列
in_tile_row_stride; // tile行跨度
// 修正边缘block尺寸
if (block_row == row_boundary)
{
cur_in_block_height = BLOCK_HEIGHT + row_edge + kernelH - 1;
}
if (block_col == col_boundary)
{
cur_in_block_width = BLOCK_WIDTH + col_edge + kernelW - 1;
}
in_tile_thread_per_row = cur_in_block_width / single_trans_ele_num;
in_tile_row_start = tid / in_tile_thread_per_row;
in_tile_col = tid % in_tile_thread_per_row * single_trans_ele_num;
in_tile_row_stride = thread_num_per_block / in_tile_thread_per_row;
3.2.1 “block”设计与修正
不要急着头大,我们逐个说明,首先看顶头部分的变量,是关于限制范围的
因为我们要首先确定一个block内的线程要负责多少元素呢,因此需要界定这样的范围
我们前面只提到了block涉及到的in范围是扩大了一圈的,其实你的in矩阵相对于out矩阵也是多了一圈的
当多的这么一圈不能构成新的block时,那么注定我们的block网格是不能覆盖到out矩阵的!
我们还是上图比较直观
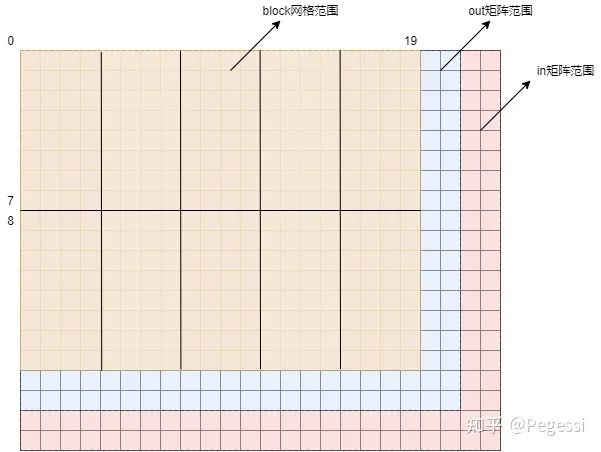
咱们的block网格只有16×20这么大,out矩阵有18×22这么大,明显可以看到蓝色的两条
是不足以构成新的block的,那么还有红色的部分,就是in矩阵的大小了,可以看到有20×24这么大
而我们的block是建立在out矩阵上的,所以我们起码也要覆盖到蓝色矩阵的所有范围吧
那么在不修改block尺寸的情况下,最简单的方法就是人为地去修正这些特定block的大小啦
修正后的block应该是这个样子的
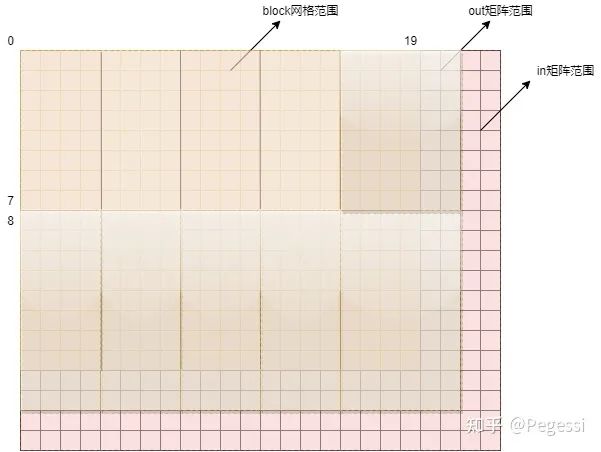
修正后的block把out全覆盖了~
怎么修正呢?无非就是利用block位序去判断并修改尺寸啦,即这两行代码
// 修正边缘block尺寸
if (block_row == row_boundary)
{
cur_in_block_height = BLOCK_HEIGHT + row_edge + kernelH - 1;
}
if (block_col == col_boundary)
{
cur_in_block_width = BLOCK_WIDTH + col_edge + kernelW - 1;
}
结合图片,是不是这些变量的概念就清晰了起来
注意我们所有变量都是有一个in的标识,这是标注in矩阵的范围
out矩阵的划分自然是有out的标识,且步骤都是一样的,只不过需要补的范围不太一样罢了
3.2.2 线程行为指定
还有一段代码我们没有解释,是这一段(thread_num_per_block本文默认为32,没有修改)
in_tile_thread_per_row = cur_in_block_width / single_trans_ele_num; in_tile_row_start = tid / in_tile_thread_per_row; in_tile_col = tid % in_tile_thread_per_row * single_trans_ele_num; in_tile_row_stride = thread_num_per_block / in_tile_thread_per_row;
这段我觉得是最抽象的部分也恰恰是最为精华的设计,首先要明确,是通过行里面的小片/tile作为线程处理的最小单元来进行设计的
其实变量名已经做了一部分的解释,可以大概解释为如下的含义
in_tile_thread_per_row 一行里面会有多少个tile
in_tile_row_start 当前线程负责的tile的起始行号
in_tile_col 当前线程负责的列号
in_tile_row_stride 如果还有元素要处理,那么需要跳过的行数/stride
好像不是那么的直观,我们再上一张图
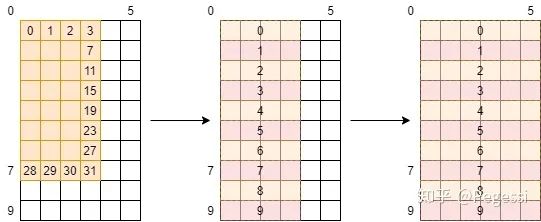
左面是我们的block与in矩阵的关系,我们要把他都转移过来,且利用了fetch_float4的向量指令(也是single_trans_ele_num设置为4的原因)
以7号线程为例,当前的in_block为10×6大小,那么上面四个变量的值分别为1,7,0,32
这个例子比较简单,可以发现一行其实是有一个半的tile的,那么需要一点点小小的修正来让每个线程
读取4+2个元素,这点小小的修正我们可以看代码
那么再来一个复杂的例子,假设我们在考虑out矩阵的事情,那么一个线程负责一个元素的话
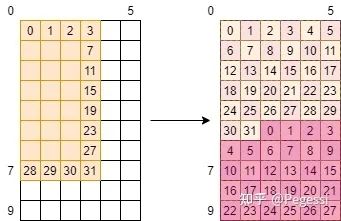
请问这种方式对嘛?
是不是直观上你感觉应该是这样的,他可以丝滑的衔接好每个元素,完成我们的分配~
那么给出我们利用这个均分思想让每个线程负责任务的代码如下,大家再想一想分配后的图像
for (int i = 0; i < cur_in_block_height && in_tile_row_start < cur_in_block_height;
i += in_tile_row_stride)
{
/*do something*/
}
浅浅一个for循环,只不过所有条件都是我们仔细设计的,循环内部就是每个线程根据这些位序
去对应的显存位置上对数据一通操作罢了
那么注意部分,线程在跨过一个stride时,这个单位是不是row?那么意味着0号线程在下次任务会踩到30号的位置!如下图所示
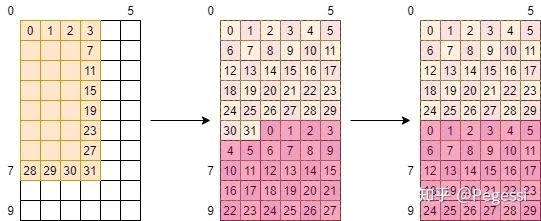
实际上的线程分配
这样才是正确的线程操作顺序,当然由于我们是通过CUDA并行计算的,实际上上半部分是并行的,下半部分是在0-29号线程完成了上面的任务后才进行计算的(注意他们是32个一组/warp调度上来执行的)
这样其实有个小隐患,30号和31号以及0,1号会对这两个位置上重复进行操作,如果他们的行为不一致的话
会导致我们的结果出错,本例中他们的行为是一致的,故无所谓先后
通过这样的机制,我们可以指定每个线程负责的元素位置以及个数(tile大小),灵活地应用于不同的任务!
3.3 预取机制
这部分就是很基本的数据预取,计算的效率远远大于访存,计算时读取数据进来,完成基本的运算
(复杂运算也不是一行代码可以解决的)
再把结果存到对应位置,我们发现是不是即使是计算你也需要访存,节省访存开销是十分重要的
整体的数据传输逻辑是GMEM->SMEM->register->GMEM->MEM
并没有使用到Constant Memory和Texture Memory,那么结合数据预取的机制下
整体的框架如下方伪代码所示
初始化我们所需要的所有变量并修正block规模;
分配好shared memory用于加速访存;
// 预读取第一个channel的数据
for (int i = 0; i < cur_in_block_height && in_tile_row_start < cur_in_block_height;
i += in_tile_row_stride)
{
把in中的数据从GMEM转到SMEM;
}
// 预读取第一个kernel的数据 可以使用很简单的读取策略 因为数据很少
if (thread_row >= 0 && thread_row < KERNEL_HEIGHT && thread_col == 0)
{
把kernel的数据从GMEM转到SMEM;
}
__syncthreads();
// 这里oc在外ic在内的设计是为了方便写回
for (int oc = 0; oc < outC; oc++)
{
for (int ic = 0; ic < inC; ic++)
{
// i,j 是相当于当前block起始位置而言
// 用ic的每个block去对oc的kernel进行计算
for (int i = 0; i < cur_out_block_height && (out_tile_row_start + i) < cur_out_block_height;
i += out_tile_row_stride)
{
计算当前ic与oc的结果,存到register;
}
// 读取下一个in channel数据 3,932,160
if (ic + 1 < inC)
{
for (int i = 0; i < cur_in_block_height && in_tile_row_start < cur_in_block_height;
i += in_tile_row_stride)
{
读取下一个channel的数据;
}
}
__syncthreads();
}
if (oc + 1 < outC)
{
读取下一个kernel数据;
}
__syncthreads();
// 注意这样的循环顺序下已经完成了一个outC的计算
for (int i = 0; i < cur_out_block_height && (out_tile_row_start + i) < cur_out_block_height; i += out_tile_row_stride;)
{
写回当前outC的数据;
}
// 预读取下一个in channel数据 需要注意这时候要从头读了
for (int i = 0; i < cur_in_block_height && in_tile_row_start < cur_in_block_height;
i += in_tile_row_stride)
{
读取第一个channel的数据;
}
}
到这里其实我们就完成了大部分内容了,整体骨架就是这样,其余就是一些细节上的下标计算问题了
3.4 一些杂项却又需要细节
3.4.1 中间结果存储设计
可以看到我们的伪代码中循环顺序是先oc再ic
可以想象一下,如果你先ic再oc的话,这样确实是我们只需要遍历一遍ic,oc多次遍历
但是我们也要考虑写回部分,写回你还需要单独再去写,理论上先ic的话会快一些
这里就不给大家放图了,读者可以自己想象一下两种计算顺序的区别
需要注意的是
线程能利用的硬件资源是有限的,一个warp共用一个SM上的寄存器,具体到每个线程大概32-255个寄存器(来源于chatGPT,不严谨,需要核实,后面gpt又说v100一个线程可以用800个..)
总之我们还是能少用就少用几个
当register存不下我们这些中间变量,就会放到local memory中
所谓的local memory是位于GMEM上的,如果发生这种情况,每次读取中间结果
你还得跑到GMEM上去访存,是非常之浪费时间的
两种循环其实需要的register数目都是oc×2(2是因为你一个线程要负责好几个位置的)
出于修正考虑,哥们儿直接开4倍,保证不会越界
3.4.2 下标计算
这部分其实,你串行算的明白,你并行就算的明白,我们举几个例子来说明一下
FETCH_FLOAT4(load_reg[0]) = FETCH_FLOAT4(in[begin_pos + OFFSET(in_tile_row_start + i, in_tile_col, inW)]); s_in[in_tile_row_start + i][in_tile_col] = load_reg[0]; s_in[in_tile_row_start + i][in_tile_col + 1] = load_reg[1]; s_in[in_tile_row_start + i][in_tile_col + 2] = load_reg[2]; s_in[in_tile_row_start + i][in_tile_col + 3] = load_reg[3];
这里是利用向量指令去一次读取4个32位数据,s_in是开在SMEM上的,in是GMEM上的一位数据
那么可以看这个后面的下标
begin_pos 代表当前block的起始位序
OFFSET 是一个宏定义,代表行×一行元素数目
in[xxx] 下标其实就是当前block位置+block内的位置
再看一个写入中间结果的位置
temp_pos = i / out_tile_row_stride + j +
oc * (cur_out_block_height / out_tile_row_stride + 1);
这里要考虑到线程是在计算它负责的第几个元素,那么就要用i / out_tile_row_stride来判断
如果处理多个元素,那你还得用j来控制一下当前是第几个元素
还要考虑到不同的oc,一个oc内负责的元素有cur_out_block_height / out_tile_row_stride +1这么多个
我们再看一个
out_pos = oc * outH * outW +
block_row * BLOCK_HEIGHT * outW + block_col * BLOCK_WIDTH + OFFSET(out_tile_row_start + i, out_tile_col + j, outW);
首先略过几个oc的范围,再计算当前block的起始位置,再计算上block内的相对位置
每个下标都要明白其计算的含义,本例中有很多公共表达式没有提取出来提前计算,会影响一定性能
3.6 性能测试
虽然是娱乐测试,但是也严谨一点,可以发现这个代码会受channel数目影响很大
代码还有一点小bug,不过不影响你执行,大家可能会发现(亟待修复)
不同数据规模下性能在cudnn的1/10到10倍上下横跳,有空给大家测一下放个完整的图。
编辑:黄飞
-
第60章 如何在对话框上绘制2D图形2016-10-18 0
-
2D卷积的行缓冲区的延迟是多少?2020-05-18 0
-
《 AI加速器架构设计与实现》+第一章卷积神经网络观后感2023-09-11 0
-
卷积解算子族的乘积扰动2009-10-26 685
-
2D仿真培训2016-11-17 769
-
2D到3D视频自动转换系统2018-03-06 1459
-
谷歌研究人员利用3D卷积网络打造视频生成新系统2019-06-02 3322
-
CUDA学习笔记第一篇:一个基本的CUDA C程序2020-12-14 912
-
PyTorch如何实现自定义CUDA算子并调用的方法且测量CUDA程序耗时2021-03-30 4516
-
Laplacian算子的硬件实现及结果2022-07-21 1110
-
2d封装库Altium2022-09-20 385
-
解析OneFlow Element-Wise算子实现方法2022-12-12 1577
-
2D中值滤波算法的设计实现2023-07-12 968
-
2D与3D视觉技术的比较2023-12-21 1143
-
一文了解3D视觉和2D视觉的区别2023-12-25 3058
全部0条评论

快来发表一下你的评论吧 !

