

四足机器人周期函数效果演示
描述
这里简单利用一个线性函数进行演示
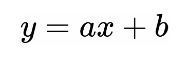
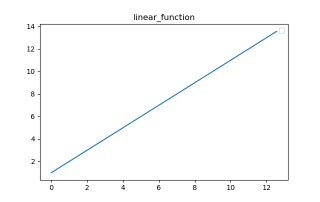
取a=1,b=1,其图像随时间变化如下:
利用周期函数对时间进行调整,可以使其变成周期函数,设定周期为2s,时长为10s,其图像如下:
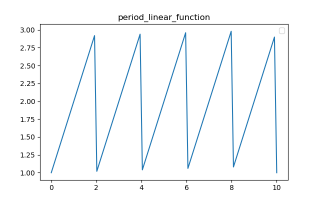
从图像可以看出,刚好为5个周期,一个周期为一个尖角。接下来,为更好的观察各曲线相位,我们设定该直线函数的3个周期,其相位差(offset)分别为[0,1,3,4],图像如下:
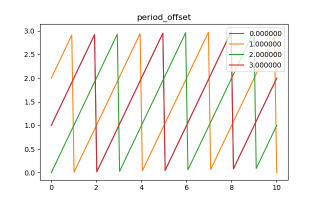
从上图可以看出,我们的“尖角”会根据相位差,向前或向后平移。此方法对所有函数均适用,以下为利用sin函数进行的测试效果:
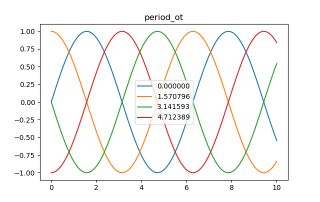
测试用代码:
import numpy as np
import matplotlib.pyplot as plt
T = 2*np.pi
t = np.linspace(0, 10, 100)
offset = [0, 0.5*np.pi, np.pi, 1.5*np.pi]
# offset = [0]*4
phi_offset = []
def linear_fun(x):
return x+1
def linear_draw():
plt.title('linear_function')
plt.plot(t, linear_fun(t))
def single_period():
plt.title('period_linear_function')
plt.plot(t, linear_fun(t % T))
def period_draw():
plt.title('period_ot')
for i in range(len(offset)):
phi_offset.append(np.sin((t+offset[i]) % T))
plt.plot(t, phi_offset[i], label='%f' % offset[i])
period_draw()
plt.legend()
plt.show()
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
四足步行机器人的弯道行走2012-08-12 0
-
双足机器人2013-11-25 0
-
stm32红外六足机器人2014-03-27 0
-
六足机器人2014-07-28 0
-
【OK210申请】四足轮式机器人2015-06-25 0
-
什么是龙人四足机器人?2016-03-24 0
-
四足仿生机器人2016-08-19 0
-
MATLAB多足步行机器人动画演示2017-04-23 0
-
四足机器人2018-09-29 0
-
求六足机器人的图纸2019-03-26 0
-
四足机器人的机构设计2021-09-15 0
-
如何完整的组装四足机器人?2021-09-24 0
-
ANYmal四足机器人的相关资料推荐2021-12-31 0
-
四足机器人遍地开花,四足机器人的市场有多大2022-04-06 1926
-
四足机器人步态规划与接触状态2023-11-16 800
全部0条评论

快来发表一下你的评论吧 !

