

揭示大模型剪枝技术的原理与发展
描述
当你听到「剪枝」二字,或许会联想到园丁修整枝叶的情景。而在 AI 大模型领域,这个词有着特殊的含义 —— 它是一种通过“精简”来提升大模型效率的关键技术。随着 GPT、LLaMA 等大模型规模的持续膨胀,如何在保持性能的同时降低资源消耗,已成为亟待解决的难题。本文将揭示大模型剪枝技术的原理与发展,带你一次性读懂剪枝。
随着人工智能的快速发展,大模型以其卓越的性能在众多领域中占据了重要地位。然而,大模型惊人的参数规模也带来了一系列挑战,如高昂的训练成本、巨大的存储需求和推理时的计算负担。为了解决这些问题,大模型剪枝技术应运而生,成为压缩大模型的关键手段。本文将简要介绍大模型剪枝技术的背景及原理、代表性方法和研究进展。
背景及原理
当今大模型的“身躯”越来越庞大,对资源的需求也日益增加。如 LLaMA 3.1,且不说其训练算力高达 24000 块 H100,训练数据量高达 15T tokens(Qwen 2.5 在 18T tokens 的数据集上进行了预训练,成为目前训练数据最多的开源大模型),单看表 1 和表 2 中 LLaMA 3.1 在推理和微调时的内存需求,对普通用户而言就是难以承受之重。这些庞大的需求不仅对硬件资源提出了极高的要求,也限制了模型的可扩展性和实用性。大模型剪枝技术通过减少模型中的参数数量,旨在降低这些需求,同时尽量保持模型的性能。
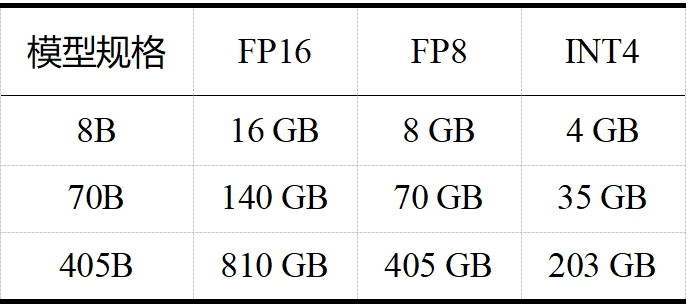
表 1 LLaMA 3.1 推理内存需求(不包括 KV 缓存)
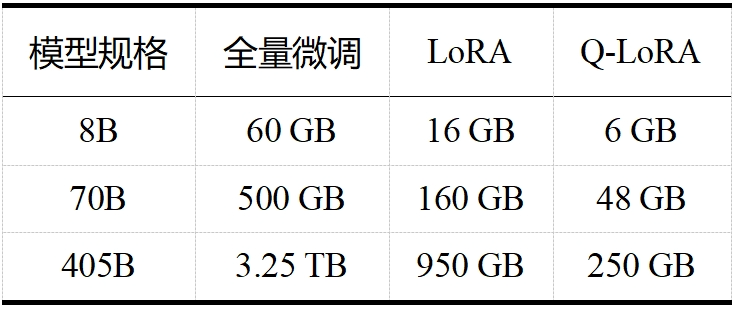
表 2 LLaMA 3.1 微调内存需求
剪枝“流派”的开山鼻祖是图灵奖得主、深度学习“三巨头”之一 Yann LeCun,他在 1989 年 NeurIPS 会议上发表的《Optimal Brain Damage》[1]是第一篇剪枝工作。后来剪枝“流派”逐渐开枝散叶,如今可主要分为两大类:非结构化剪枝和结构化剪枝。非结构化剪枝通过移除单个权重或神经元得到稀疏权重矩阵,这种方法易于实现且性能指标较高,但需要专门的硬件或软件支持来加速模型;结构化剪枝通过去除基于特定规则的连接来实现,如层级剪枝、块级剪枝等,这种方法不需要专门的软硬件支持,但算法更为复杂。
两类剪枝方法在大模型上都有很多的尝试和应用,但考虑到通用性,我们主要关注结构化剪枝,本文的第二部分也将主要介绍 LLM 结构化剪枝的经典文章 LLM-Pruner。
下面谈一谈剪枝的理论基础。首先,所谓的理论基础只是暂时的,在一个高速发展的学科中,很难确保今天的理论不会被明天的实验推翻。在传统上,人们一直认为剪枝的基础是 DNN 的过参数化,即深度神经网络参数比拟合训练数据所需参数更多,可以剪去一部分以降低网络复杂度而尽量不影响其性能。 在 2019 年,有学者提出了彩票假设(ICLR 2019 best paper)[2]:一个随机初始化的神经网络里包括一个子网络,当该子网络被单独训练时,能在最多相同迭代次数后达到原始网络训练后的性能——就好比一堆彩票中存在一个中奖子集,只要买了这个子集就能获得最大收益。 随后,又有学者在《What’s Hidden in a Randomly Weighted Neural Network?》中提出了“近似加强版”彩票假设(CVPR 2020)[3]:在一个随机权重的足够过参数化的神经网络中,存在一个子网络,无需训练,其性能与相同参数量训练过的网络相当。 再随后,又有学者声称自己证明了这个“近似加强版”的彩票假设,并在标题里宣称 Pruning is all you need(ICML 2020)[4]。也就是说,如图 1 所示,以后不需要训练了,我们只用找一个足够大的网络,剪啊剪啊就能得到一个性能很好的子网络。这个说法如果成立当然是极好的,因为基于梯度的优化算法训练时间长,且是次优的,但问题在于缺乏有效的纯剪枝算法,所以目前剪枝的基本流程还是:训练、剪枝、微调。另外,作者是用二值小网络+推广证明的,太过理想化,而且没有考虑非线性的情况。近年来,虽然彩票假设及其衍生理论在一些研究领域取得了进展,例如图中奖彩票(KDD 2023)[5]和对偶彩票假设(ICLR 2022)[6],但在大模型领域,我们尚未观察到具有显著影响力的研究工作。

图 1 LLaMA 3.1 微调内存需求
代表性方法:LLM-Pruner
本节将以首个针对大模型的结构化剪枝框架 —— LLM-Pruner(NeurIPS 2023)[7]为例,介绍大模型剪枝的基本流程。该框架特点为任务无关的压缩、数据需求量少、快速和全自动操作,主要包括以下三个步骤:(1)分组阶段
本阶段的主要工作是根据依赖性准则,将 LLM 中互相依赖的神经元划分为一组。依赖性准则为:若 i 是 j 的唯一前驱,则 j 依赖于 i;若 j 是 i 的唯一后继,则 i 依赖于 j。在具体操作中,需要分别将网络中每个神经元作为初始节点,依赖关系沿方向传导,传导过程中遍历的神经元为一组,一组需同时剪枝。以图 2 中 Group Type B(即 MHA,多头注意力)为例,从 Head 1 开始传导,Head 1 是上面两个虚线圈神经元的唯一前驱,是下面六个虚线圈神经元的唯一后继,它们都依赖于 Head 1,故被划分为一组。
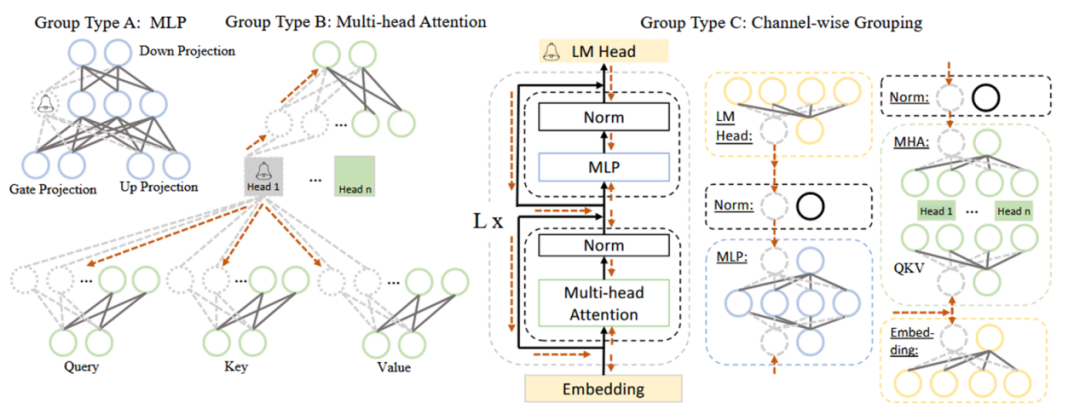
图 2 LLaMA 中耦合结构的简化示例 (2)评估阶段
本阶段的主要工作是根据重要性准则评估每个组对模型整体性能的贡献,贡献小的组将被修剪。常见的重要性准则有:L1 范数(向量中各元素绝对值之和)、L2 范数(向量中各元素平方和的开平方)、损失函数的 Taylor 展开一阶项、损失函数的 Taylor 展开二阶项等。LLM-Pruner 采用损失函数的 Taylor 展开来计算重要性,并提出了两条计算组重要性的路径:权重向量级别和单个参数级别。
权重向量级别的重要性公式如下所示, 代表每个神经元的权重向量,H 是 Hessian 矩阵, 表示 next-token prediction loss。一般来说由于模型在训练数据集上已经收敛,即 , 所以一阶项通常为 0 。然而,由于 LLM-Pruner 所用数据集 D 并不是原始训练数据,故 。同时,由于 Hessian 矩阵的计算复杂度过高, 所以只计算了一阶项。
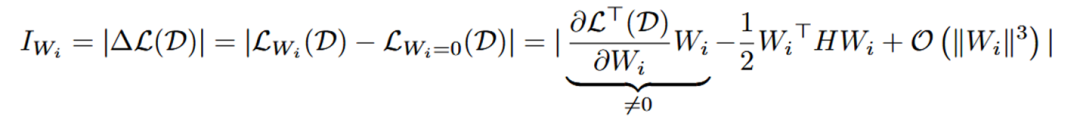
单个参数级别的重要性公式如下所示, 内的每个参数都被独立地评估其重要性,其中 Hessian 矩阵用 Fisher 信息矩阵进行了近似。在 LLM-Pruner 的源码中,这两个公式被如图 3 所示的代码片段表示。
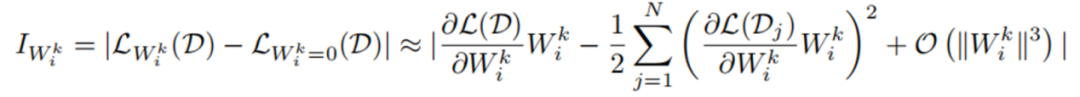
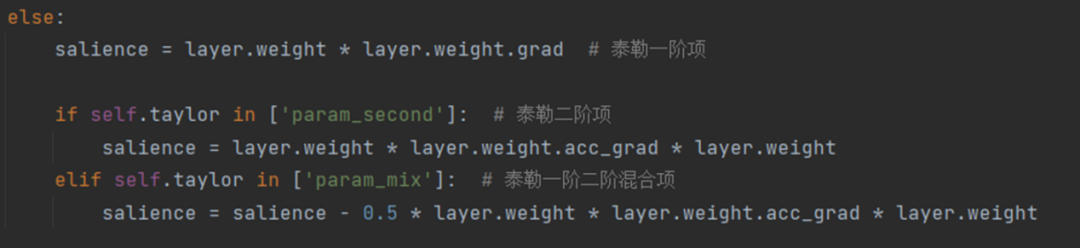
图 3 评估重要性的源码
最后,通过对每组内权重向量或参数的重要性进行累加/累乘/取最大值/取最后一层值,就得到了每组的重要性,再按剪枝率剪去重要性低的组即可。
(3)微调阶段
本阶段的主要工作是使用 LoRA 微调模型中每个可学习的参数矩阵 W,以减轻剪枝带来的性能损失。LoRA 的公式为 W + ∆W = W + BA,其具体步骤如图 4 所示:
① 在模型的特定层中用 Wd×k + ΔWd×k 替换原有的权重矩阵 Wd×k,并把矩阵 ∆Wd×k 分解成降维矩阵 Ad×r 和升维矩阵 Br×k,r << min(d, k)。
② 将 A 随机高斯初始化,B 置为 0,冻结预训练模型的参数 W,只训练矩阵 A 和矩阵 B。
③ 训练完成后,将 B 矩阵与 A 矩阵相乘再与矩阵 W 相加,作为微调后的模型参数。
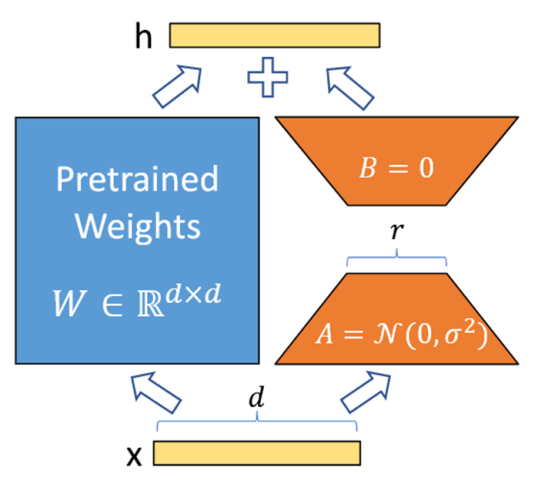
图 4 LoRA 基本步骤
根据表 3 的实验结果,剪枝 20% 后,模型的性能为原模型的 89.8%,经过 LoRA 微调后,性能可提升至原模型的 94.97%。在大多数数据集上,剪枝后的 5.4B LLaMA 甚至优于 ChatGLM-6B,所以如果需要一个具有定制尺寸的更小的模型,理论上用 LLM-Pruner 剪枝一个比再训练一个成本更低效果更好。
然而,根据表 4 的数据显示,剪枝 50% 后模型表现并不理想,LoRA 微调后综合指标也仅为原模型 77.44%,性能下降幅度较大。如何进行高剪枝率的大模型结构化剪枝,仍是一个具有挑战性的问题。
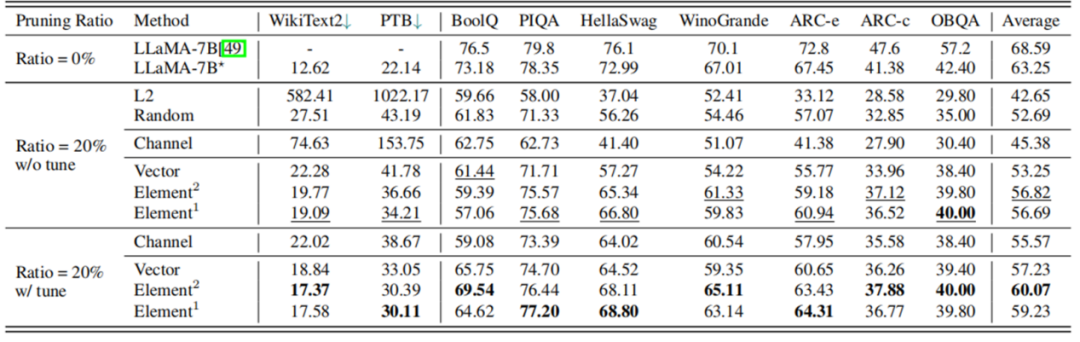
表 3 LLaMA-7B 剪枝 20% 前后性能对比
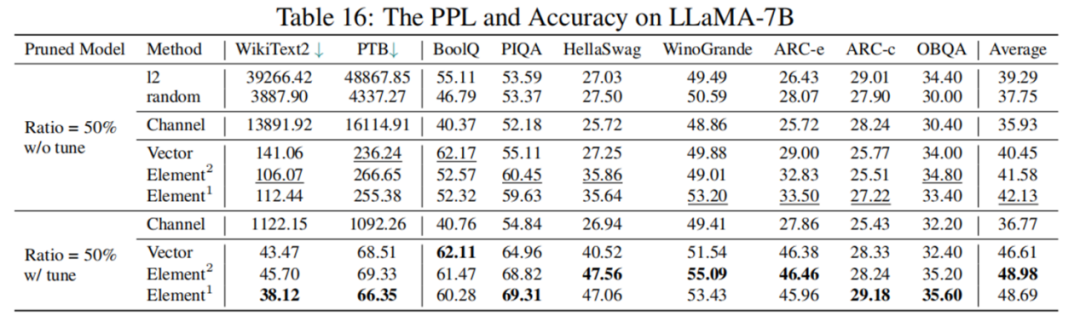
表 4 LLaMA-7B 剪枝 50% 前后性能对比
研究进展
大模型剪枝技术已经成为近两年的研究热点,无论是在工业界还是学术界,都有许多研究人员投身于这一领域——这一点从表 5 和表 6 中可以明显看出,而表格中列出的论文只是众多大模型剪枝研究工作中的一小部分。除此之外,还有学者提出了介于结构化剪枝和非结构化剪枝之间的半结构化剪枝,如 Nvidia 的 N:M 稀疏化,就是每 M 个连续元素留下 N 个非零元素,但与前两者相比目前相关探索较少。随着研究的不断深入和技术的持续进步,我们有理由相信,剪枝将继续在大模型领域扮演重要的角色,并推动大模型技术的创新和发展。
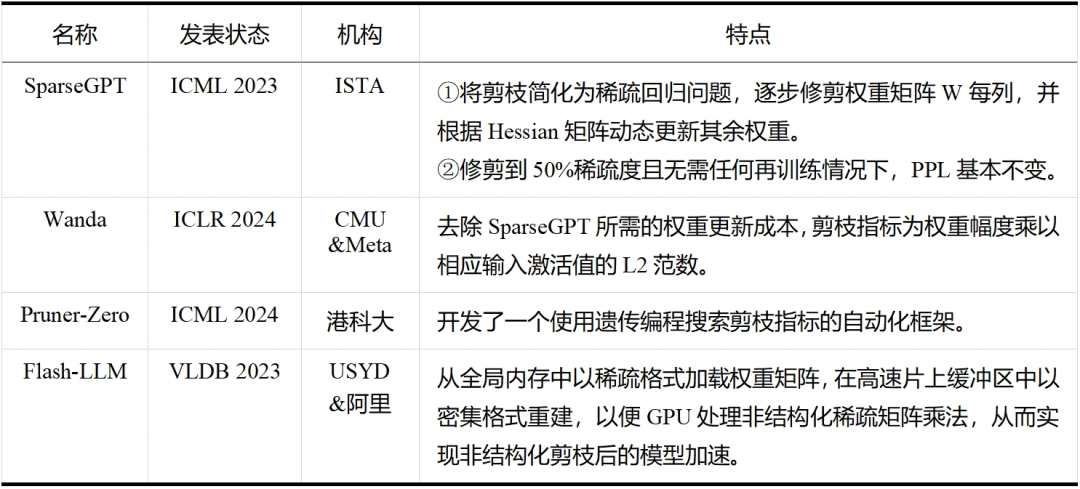
表 5 大模型非结构化剪枝
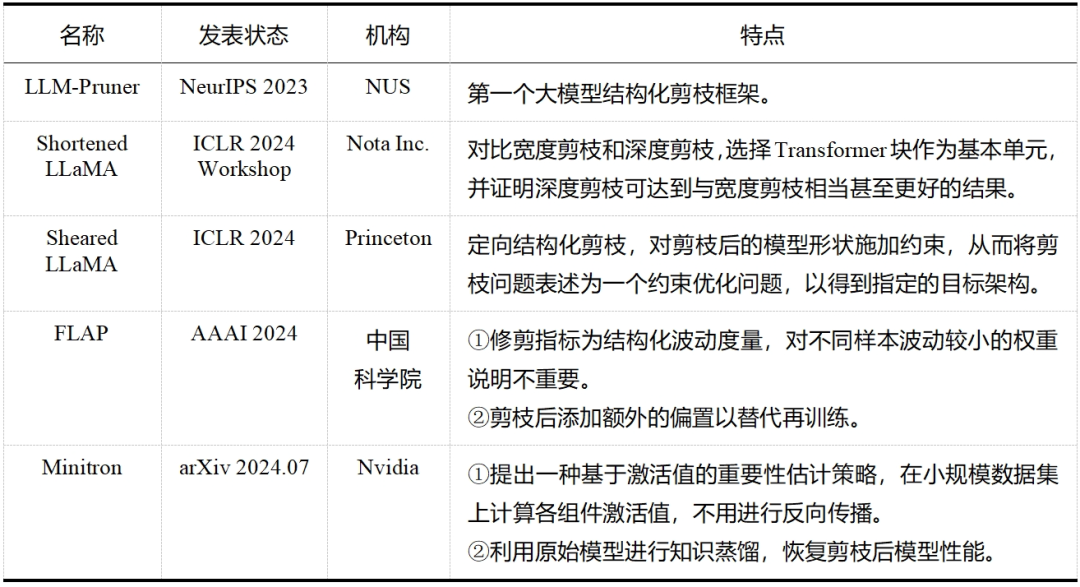
表 6 大模型结构化剪枝
-
《移动终端人工智能技术与应用开发》+理论学习2023-02-27 0
-
量化剪枝概念格在服务贸易挖掘中的应用2010-01-22 464
-
一种新型的决策树剪枝优化算法2017-11-30 739
-
基于影响度剪枝的ELM分类算法2017-12-01 671
-
如何使用剪枝优化与索引求交改进Eclat算法2018-12-19 785
-
基于深度神经网络的结构化剪枝算法2021-03-10 752
-
嵌入式设备的YOLO网络剪枝算法2021-03-11 830
-
神经网络模型剪枝后泛化能力的验证方案2021-05-25 609
-
基于ReliefF剪枝的多标记分类算法综述2021-06-24 614
-
通过 TensorFlow模型优化工具包TF MOT剪枝API2021-08-16 4891
-
缓解模型训练成本过高的问题2022-05-10 1520
-
DepGraph:任意架构的结构化剪枝,CNN、Transformer、GNN等都适用!2023-03-29 4333
-
CVPR 2023:基于可恢复性度量的少样本剪枝方法2023-05-10 1128
-
NVIDIA 自动驾驶实验室:基于剪枝的 AI 模型优化2023-09-19 754
-
张宏江深度解析:大模型技术发展的八大观察点2024-03-14 235
全部0条评论

快来发表一下你的评论吧 !

