一文详解物理信息神经网络

物理信息神经网络 (PINN) 是一种神经网络，它将微分方程描述的物理定律纳入其损失函数中，以引导学习过程得出更符合基本物理定律的解。

PINN 可用于：

逼近偏微分方程 (PDE) 和常微分方程 (ODE) 的解。

求解逆问题，例如基于有限的数据估计模型参数。

使用 Deep Learning Toolbox，您可以构建和训练 PINN，从而实现快速预测性分析。您可以将 PINN 与 MATLAB 和 Simulink 相集成，以进行系统级仿真、控制设计和设计优化。

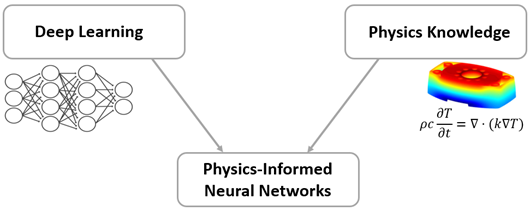
物理信息神经网络 (PINN) 在深度学习模型的训练中包含支配现实的物理定律，从而能够对复杂现象进行预测和建模，同时遵守基本物理原理。

PINN 的优点

PINN 是一类物理信息机器学习方法，可将物理知识与数据无缝集成。在求解涉及 PDE 和 ODE 的问题时，通常会将 PINN 与纯数据驱动方法和传统数值方法进行比较。

纯粹数据驱动方法仅从输入和输出数据中学习数学关系，而 PINN 与之不同：

使用先验物理知识。

在训练数据集之外作出更准确的预测。

在训练数据有限或含噪的情况下更有效。

与求解微分方程的传统数值方法(如用于 PDE 的有限元分析)不同，PINN 具有以下特点：

无网格。

能逼近高维 PDE 解。

可求解缺失模型参数，如未知的 PDE 或 ODE 系数。

可求解没有边界数据的不适定问题。

可轻松纳入稀疏或含噪测量。

虽然 PINN 与纯粹数据驱动方法和传统数值方法相比具有潜在优点，但也存在一些限制和挑战，其中包括：

有限收敛理论

缺乏统一的训练策略

计算高阶导数的计算成本

难以学习 PDE 解的高频和多尺度分量

然而，PINN 是充满活力的研究领域，并且在不断进步，有望解决和克服当前面临的上述挑战和限制。

如何在 PINN、数据驱动方法和传统数值方法之间作出选择，取决于您的具体应用。下表总结了每种方法的优点和限制。

特征比较：PINN、纯数据驱动方法(仅从输入-输出数据中学习数学关系)和传统数值方法(如用于逼近 PDE 解的有限元分析)。

PINN 传统神经网络的区别

与传统神经网络的不同之处在于，PINN 能够以微分方程形式纳入有关问题的先验专业知识。这些附加信息使 PINN 能够在给定的测量数据之外作出更准确的预测。此外，额外的物理知识还能在存在含噪测量数据的情况下对预测解进行正则化处理，从而使 PINN 能够基于真正的基本信号进行学习，而不是对含噪数据过拟合。

例如，假设已收集某系统的含噪测量值 θ_{meas}，目标是用前馈人工神经网络预测系统的将来值 θ_{pred}。该网络使用现有测量值进行训练，并将用于预测未知的将来值。训练回归神经网络通常需要尽量减小神经网络预测值与所提供测量值之间的均方误差。

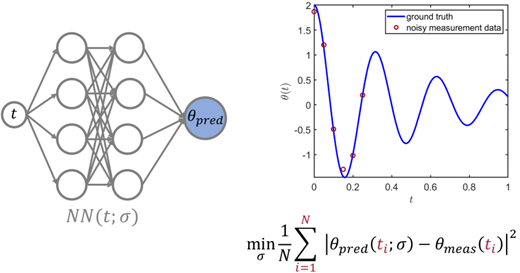
传统的神经网络会调整参数，以尽量减小网络预测值与观测的测量之间的误差。

神经网络很难准确预测训练数据之外的系统值。

使用 Deep Learning Toolbox 中的 trainnet 函数训练的原始神经网络会过拟合含噪测量值，在 t 超出可用范围时表现不佳。

获取更多数据可以提高预测效果，但这种方法可能成本过高，或对许多应用来说根本不适用。然而，领域专家往往对控制所研究系统的基本物理过程有更深入的了解。具体来说，在这里，测量值表示的是起重机上摆动的有效负载相对于垂直线的位移角度。此过程可以简单地用阻尼摆来表示，对于小角度来说，可以用线性二阶微分方程来近似建模：

θ^{''}(t)+2βθ^{′}(t)+ω^{2}_{0}θ(t)=0

PINN 并没有忽略这些知识，而是将微分方程作为附加的物理信息项纳入损失函数中。PINN 在域中的其他点上计算微分方程的残差，这为 PINN 提供了更多信息，而无需更多测量值。此简单示例当然可以通过解析方式求解，但它旨在说明 PINN 背后的概念。

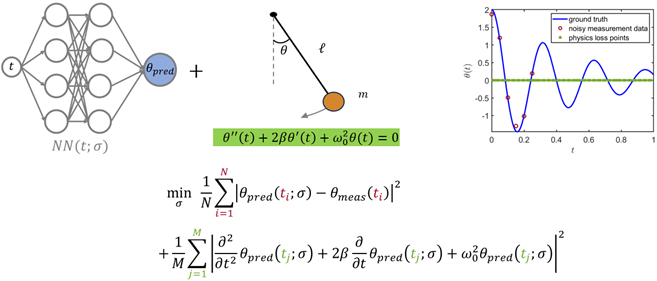
Deep Learning Toolbox 中提供的 PINN 可调整其参数，以平衡网络的预测值与观测的测量值之间的误差最小化和物理损失。

在训练过程中，PINN 会在拟合给定测量值和基本物理过程之间找到平衡点。

与传统神经网络相比，使用 Deep Learning Toolbox 创建和训练的 PINN 能在测量数据之外作出更好的预测，抗噪的稳定性也更强。(请参阅 MATLAB 代码。)

通过纳入额外的物理损失项，PINN 在存在含噪测量值和无测量数据情况下的预测效果优于传统神经网络。

PINN 的工作原理

PINN 使用优化算法以迭代方式更新神经网络参数，直到指定的物理信息损失函数值降至可接受的水平，从而推动网络趋向微分方程的解。

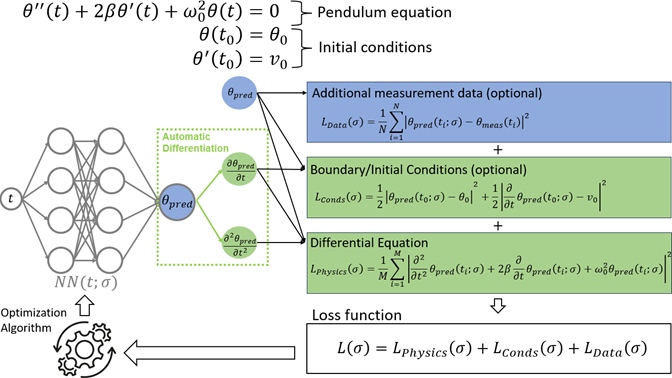
在针对摆方程这样的 ODE 训练 PINN 时，优化算法会调整神经网络的参数，以将损失函数(包括自动微分 (AD) 的微分方程残差、边界和初始条件，以及可选的其他标注数据)降至可接受的水平。

PINN 包括损失函数 L，由以下几个项组成：物理信息损失项 L_{Physics};计算网络预测的值与初始和/或边界数据规定的值之间误差的可选项 L_{Conds};以及其他额外的测量值 L_{Data}。物理信息损失项使用自动微分 (AD) 或其他数值微分法计算微分方程在域中各点的残差。由于物理信息项并不计算预测值与目标值之间的误差，因此可以将此项视为无监督损失项，也就是说，可以使用域中的任何点对网络进行训练，即使没有在这些点上的测量值也是如此。

PINN 于 2017 年首次推出，现在有许多变体，其中包括：

贝叶斯 PINN (BPINN)，它们使用贝叶斯框架支持不确定性量化

变分 PINN (VPINN)，它们将 PDE 的弱形式纳入损失函数中

一阶公式化 PINN (FO-PINN)，它们在求解高阶 PDE 时比标准 PINN 更快、更准确

此外，PINN 还可与不同神经网络架构结合使用，如图神经网络 (GNN)、傅里叶神经算子 (FNO)、深度算子网络 (DeepONet) 等，从而产生了出这些架构的所谓物理信息版本。

MATLAB 和 Deep Learning Toolbox 全面支持 PINN 的开发，从创建或导入不同神经网络架构，到使用 AD 定义自定义物理信息损失函数，再到使用 ADAM 或 L-BFGS 等基于梯度的优化算法进行训练，最后到使用高级 MATLAB 图形可视化解。

PINN 的应用

PINN 可充分利用深度学习的强大功能，同时改进对物理定律的遵从，这使其成为一种多功能工具，适用于完全或部分已知物理定律的应用，例如具有未知系数的 PDE 或 ODE。PINN 的应用包括：

热传递，专门用于热分布和传递过程建模。PINN 可以将用于材料和系统热过程建模的控制方程(如热方程)嵌入损失函数中。这种方法可确保解符合这些物理定律，从而得出在物理上合理的预测。此外，PINN 还能取代高成本的数值仿真，在设计优化应用中快速逼近参数化的几何形状上的温度分布。而且，PINN 还可用于逆问题以确定未知的材料属性，如热导率。

计算流体动力学 (CFD)，特别是通过在损失函数中纳入纳维-斯托克斯方程来逼近流体的速度、压力和温度场。PINN 可用于无网格正仿真以准确预测这些量;也可用于逆问题，目的是从观测的数据推断未知参数或输入，如边界条件、源项或流体属性。

结构力学，通过将弹性方程和结构动力学方程等控制物理定律直接嵌入损失函数中，求解正逆问题。这种集成使 PINN 能够准确预测各种负载和条件下的变形、应力和应变等结构响应，以及根据观测的数据识别未知的材料属性或外部负载。PINN 利用物理原理指导学习过程，可减少对大量数据集的依赖，在传统解析解不可行或数据匮乏的情况下尤其有用。PINN 的灵活性使其能够处理复杂的问题，包括非线性材料行为和多物理建模。

在使用 Deep Learning Toolbox 创建和训练 PINN 后，PINN 可与 Optimization Toolbox 无缝集成以用于设计优化、与 Simulink 连接以用于系统级仿真，还可用于其他各种应用。