优化设计-有约束复合型法-MATLAB编程求解
本文求解案例如下:
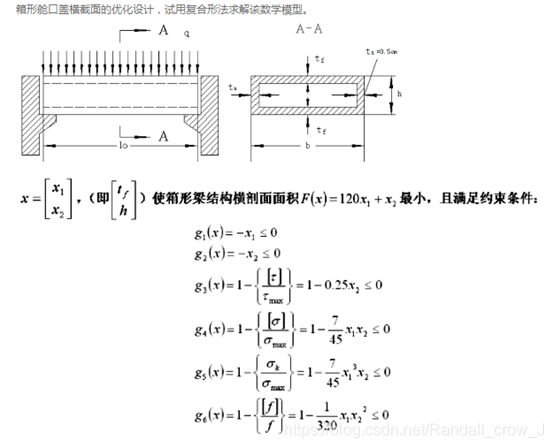
有约束复合型法迭代步骤(计算流程图)
个人编写的复合型法迭代步骤(计算流程图)如下图所示:
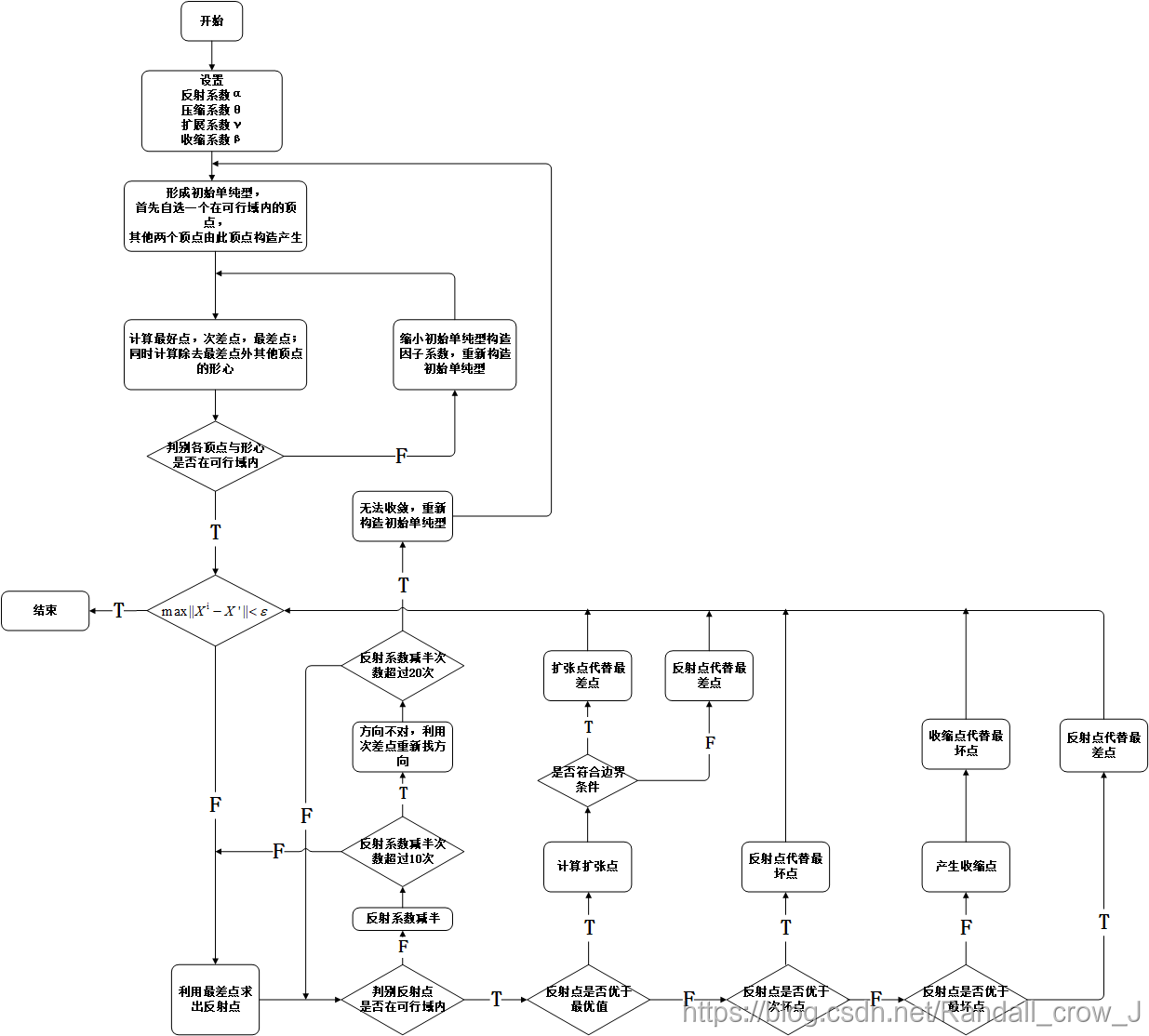
本程序增加了反射系数收缩次数的限制,在利用最差点求取反射点时,如果多次收缩反射系数后仍不能使得反射点位于可行域内(说明反射方向不利),则利用次差点进行反射点求取。若利用次差点在反射系数缩减一定次数内也无法使得反射点位于可行域内,则重新构造初始单纯型。
MATLAB主程序
主程序代码:
clear all;clc
%% 初始参数设定,求f最小值
syms x1 x2 x
f=120*x1+x2;% f 函数符号表达式
% 可行域条件在judge子函数中.m文件中
h=4; % 初始单纯形构造因子
hi=1; % 初始单纯型构造因子系数
alpha=1; % alpha 反射因子
ai=0; % 反射因子系数
gama=2; % gama 扩张因子
beta=0.5;% beta 收缩因子
eps=5;% eps 精度值
n = 0; %迭代循环次数
m = 10000; %初始精度差值
k = 0; %数据记录
g = 0; %操作记录
%% 构造初始单纯形
x0=[20 15];% 给定在可行域内初始点
x0=x0‘;
X(:,1)=x0;
Num_var_f=length(symvar(f));%二维函数
for i = 1:Num_var_f %二维函数,需要三个顶点坐标
x = zeros(Num_var_f,1);%预分配内存
x=x0;
x(i) = x0(i) + h/hi;
X(:,i+1)=x;% 将单纯形按列从左往右存储
end
for i = 1:Num_var_f+1
F_val(i)=double(subs(f,symvar(f),X(:,i)’));
end
[F_sort,F_index]=sort(F_val);%从小到大排列函数
% 最好点
f_best_0=F_sort(1);
X_best_0=X(:,F_index(1));
% 最差点
f_bad_n=F_sort(end);
X_bad_n=X(:,F_index(end));
% 次差点
f_nextbad_1n=F_sort(end-1);
X_nextbad_1n=X(:,F_index(end-1));
% 计算形心
Xc_n1=1/Num_var_f*sum(X(:,F_index(1:end-1)),2);
f_Xc_n1=double(subs(f,symvar(f),Xc_n1‘));
%% 判断顶点不在可行域内以及型心在不在可行域内
while judge(X(1,1),X(2,1))《1&&judge(X(1,2),X(2,2))《1&&judge(X(1,3),X(2,3))《1&&judge(Xc_n1(1,1),Xc_n1(2,1))《1
hi=2*hi;
for i = 1:Num_var_f %二维函数,需要三个顶点坐标
x = zeros(Num_var_f,1);%预分配内存
x=x0;
x(i) = x0(i) + h/hi;
X(:,i+1)=x;% 将单纯形存储
end
%计算函数值
for i = 1:Num_var_f+1
F_val(i)=double(subs(f,symvar(f),X(:,i)’));
end
[F_sort,F_index]=sort(F_val);%从小到大排列函数
% 最好点
f_best_0=F_sort(1);
X_best_0=X(:,F_index(1));
% 最差点
f_bad_n=F_sort(end);
X_bad_n=X(:,F_index(end));
% 次差点
f_nextbad_1n=F_sort(end-1);
X_nextbad_1n=X(:,F_index(end-1));
% 计算形心
Xc_n1=1/Num_var_f*sum(X(:,F_index(1:end-1)),2);
f_Xc_n1=double(subs(f,symvar(f),Xc_n1‘));
end
%% 循环迭代语句
while m 》 eps
%% 反射
flag = 0;
X_reflect_n2=Xc_n1+alpha*(Xc_n1-X_bad_n);
f_reflect_n2=double(subs(f,symvar(f),X_reflect_n2’));
X_reflect_n2
ai=0;
while judge(X_reflect_n2(1,1),X_reflect_n2(2,1))《1%判断反射点在不在可行域内
ai=ai+1;
if ai》10 %% 系数缩小是否过多
flag = 0;
X_reflect_n2=Xc_n1+alpha*(1/2^(ai-10))*(Xc_n1-X_nextbad_1n);
f_reflect_n2=double(subs(f,symvar(f),X_nextbad_1n‘));;%% (方向不对,利用次差点重新找方向)
if ai》20
disp(’无法收敛,请重新构造初始单纯型’);
break
end
else
flag = 0;
X_reflect_n2=Xc_n1+alpha*(1/2^ai)*(Xc_n1-X_bad_n);
f_reflect_n2=double(subs(f,symvar(f),X_reflect_n2’));
end
end
%% 反射成功
if f_reflect_n2《f_best_0 % 反射点R《最好点
%% 进行扩张
X_reflect_expand_n3=Xc_n1+gama*(Xc_n1-X_bad_n);%扩张
f_reflect_expand_n3=double(subs(f,symvar(f),X_reflect_expand_n3‘));
if f_reflect_expand_n3 《 f_best_0 &&judge( X_reflect_expand_n3(1,1),X_reflect_expand_n3(2,1))》=1%判断扩张点是否在可行域内%扩张点继续缩小
X(:,F_index(end)) = X_reflect_expand_n3; %将其作为单纯型的新顶点
g=1;%扩张点
else
X(:,F_index(end)) = X_reflect_n2; %采用扩张前的点作为单纯形的新顶点
g=0;%反射点
end
flag = 1; %反射成功标志位
end
%% 反射失败
if flag == 0 %说明没有反射成功
if f_reflect_n2 《 f_nextbad_1n %反射点《次差点
X(:,F_index(end)) = X_reflect_n2;%采用该反射点作为新的顶点
g=0;%反射点
%% 进行收缩
else % f_reflect 》= f_nextbad
X_reflect_shrink_n4=Xc_n1+beta*(X_reflect_n2-Xc_n1);% 收缩点
f_reflect_shrink_n4=double(subs(f,symvar(f),X_reflect_shrink_n4’));
X(:,F_index(end)) = X_reflect_shrink_n4;
g=2;%收缩点
end
end
%% 计算迭代完后函数序列,并计算精度
for i = 1:Num_var_f+1
F_val(i)=double(subs(f,symvar(f),X(:,i)‘));
end
[F_sort,F_index]=sort(F_val);%从小到大排列函数
% 最好点
f_best_0=F_sort(1);
X_best_0=X(:,F_index(1));
% 最差点
f_bad_n=F_sort(end);
X_bad_n=X(:,F_index(end));
% 次差点
f_nextbad_1n=F_sort(end-1);
X_nextbad_1n=X(:,F_index(end-1));
% 计算形心
Xc_n1=1/Num_var_f*sum(X(:,F_index(1:end-1)),2);
f_Xc_n1=double(subs(f,symvar(f),Xc_n1’));
% 计算精度与迭代次数
m=abs(double(subs(f,symvar(f),X(:,F_index(end))‘))-f_Xc_n1);
n=n+1;
% 运算数据记录
end
%% 结果输出
minx=X_best_0;
ff=120*X_best_0(1,1)+X_bes
约束条件判断子函数
judge子函数代码:
judge子函数如下:
function [J]=judge(x1,x2)
g1=1-0.25*x2;%
g2=1-7/45*x1*x2;
g3=1-7/45*x1^3*x2;
g4=1-1/320*x1*x2^2;%
g5=-x1;%
g6=-x2;
% 可行域条件
if g1《=0&&g2《=0&&g3《=0&&g4《=0&&g5《=0&&g6《=0
J=1
else
J=0
end
运算结果与可行域
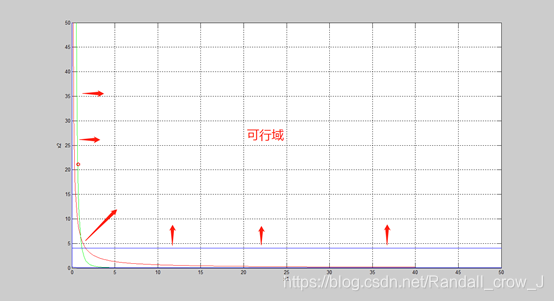
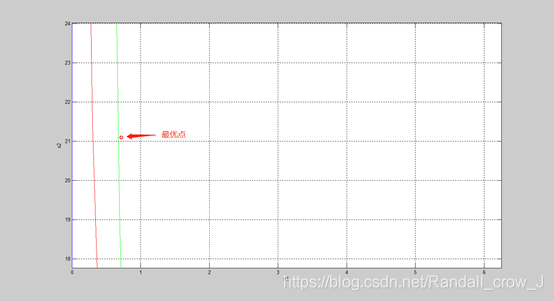
程序运行结果为:最优点(0.7217,21.0939),此时f= 107.6936。此时程序所取eps=5
可行域图与最优点于图上标记:
优化设计-有约束复合型法-MATLAB编程求解
本文求解案例如下:

有约束复合型法迭代步骤(计算流程图)
个人编写的复合型法迭代步骤(计算流程图)如下图所示:

本程序增加了反射系数收缩次数的限制,在利用最差点求取反射点时,如果多次收缩反射系数后仍不能使得反射点位于可行域内(说明反射方向不利),则利用次差点进行反射点求取。若利用次差点在反射系数缩减一定次数内也无法使得反射点位于可行域内,则重新构造初始单纯型。
MATLAB主程序
主程序代码:
clear all;clc
%% 初始参数设定,求f最小值
syms x1 x2 x
f=120*x1+x2;% f 函数符号表达式
% 可行域条件在judge子函数中.m文件中
h=4; % 初始单纯形构造因子
hi=1; % 初始单纯型构造因子系数
alpha=1; % alpha 反射因子
ai=0; % 反射因子系数
gama=2; % gama 扩张因子
beta=0.5;% beta 收缩因子
eps=5;% eps 精度值
n = 0; %迭代循环次数
m = 10000; %初始精度差值
k = 0; %数据记录
g = 0; %操作记录
%% 构造初始单纯形
x0=[20 15];% 给定在可行域内初始点
x0=x0‘;
X(:,1)=x0;
Num_var_f=length(symvar(f));%二维函数
for i = 1:Num_var_f %二维函数,需要三个顶点坐标
x = zeros(Num_var_f,1);%预分配内存
x=x0;
x(i) = x0(i) + h/hi;
X(:,i+1)=x;% 将单纯形按列从左往右存储
end
for i = 1:Num_var_f+1
F_val(i)=double(subs(f,symvar(f),X(:,i)’));
end
[F_sort,F_index]=sort(F_val);%从小到大排列函数
% 最好点
f_best_0=F_sort(1);
X_best_0=X(:,F_index(1));
% 最差点
f_bad_n=F_sort(end);
X_bad_n=X(:,F_index(end));
% 次差点
f_nextbad_1n=F_sort(end-1);
X_nextbad_1n=X(:,F_index(end-1));
% 计算形心
Xc_n1=1/Num_var_f*sum(X(:,F_index(1:end-1)),2);
f_Xc_n1=double(subs(f,symvar(f),Xc_n1‘));
%% 判断顶点不在可行域内以及型心在不在可行域内
while judge(X(1,1),X(2,1))《1&&judge(X(1,2),X(2,2))《1&&judge(X(1,3),X(2,3))《1&&judge(Xc_n1(1,1),Xc_n1(2,1))《1
hi=2*hi;
for i = 1:Num_var_f %二维函数,需要三个顶点坐标
x = zeros(Num_var_f,1);%预分配内存
x=x0;
x(i) = x0(i) + h/hi;
X(:,i+1)=x;% 将单纯形存储
end
%计算函数值
for i = 1:Num_var_f+1
F_val(i)=double(subs(f,symvar(f),X(:,i)’));
end
[F_sort,F_index]=sort(F_val);%从小到大排列函数
% 最好点
f_best_0=F_sort(1);
X_best_0=X(:,F_index(1));
% 最差点
f_bad_n=F_sort(end);
X_bad_n=X(:,F_index(end));
% 次差点
f_nextbad_1n=F_sort(end-1);
X_nextbad_1n=X(:,F_index(end-1));
% 计算形心
Xc_n1=1/Num_var_f*sum(X(:,F_index(1:end-1)),2);
f_Xc_n1=double(subs(f,symvar(f),Xc_n1‘));
end
%% 循环迭代语句
while m 》 eps
%% 反射
flag = 0;
X_reflect_n2=Xc_n1+alpha*(Xc_n1-X_bad_n);
f_reflect_n2=double(subs(f,symvar(f),X_reflect_n2’));
X_reflect_n2
ai=0;
while judge(X_reflect_n2(1,1),X_reflect_n2(2,1))《1%判断反射点在不在可行域内
ai=ai+1;
if ai》10 %% 系数缩小是否过多
flag = 0;
X_reflect_n2=Xc_n1+alpha*(1/2^(ai-10))*(Xc_n1-X_nextbad_1n);
f_reflect_n2=double(subs(f,symvar(f),X_nextbad_1n‘));;%% (方向不对,利用次差点重新找方向)
if ai》20
disp(’无法收敛,请重新构造初始单纯型’);
break
end
else
flag = 0;
X_reflect_n2=Xc_n1+alpha*(1/2^ai)*(Xc_n1-X_bad_n);
f_reflect_n2=double(subs(f,symvar(f),X_reflect_n2’));
end
end
%% 反射成功
if f_reflect_n2《f_best_0 % 反射点R《最好点
%% 进行扩张
X_reflect_expand_n3=Xc_n1+gama*(Xc_n1-X_bad_n);%扩张
f_reflect_expand_n3=double(subs(f,symvar(f),X_reflect_expand_n3‘));
if f_reflect_expand_n3 《 f_best_0 &&judge( X_reflect_expand_n3(1,1),X_reflect_expand_n3(2,1))》=1%判断扩张点是否在可行域内%扩张点继续缩小
X(:,F_index(end)) = X_reflect_expand_n3; %将其作为单纯型的新顶点
g=1;%扩张点
else
X(:,F_index(end)) = X_reflect_n2; %采用扩张前的点作为单纯形的新顶点
g=0;%反射点
end
flag = 1; %反射成功标志位
end
%% 反射失败
if flag == 0 %说明没有反射成功
if f_reflect_n2 《 f_nextbad_1n %反射点《次差点
X(:,F_index(end)) = X_reflect_n2;%采用该反射点作为新的顶点
g=0;%反射点
%% 进行收缩
else % f_reflect 》= f_nextbad
X_reflect_shrink_n4=Xc_n1+beta*(X_reflect_n2-Xc_n1);% 收缩点
f_reflect_shrink_n4=double(subs(f,symvar(f),X_reflect_shrink_n4’));
X(:,F_index(end)) = X_reflect_shrink_n4;
g=2;%收缩点
end
end
%% 计算迭代完后函数序列,并计算精度
for i = 1:Num_var_f+1
F_val(i)=double(subs(f,symvar(f),X(:,i)‘));
end
[F_sort,F_index]=sort(F_val);%从小到大排列函数
% 最好点
f_best_0=F_sort(1);
X_best_0=X(:,F_index(1));
% 最差点
f_bad_n=F_sort(end);
X_bad_n=X(:,F_index(end));
% 次差点
f_nextbad_1n=F_sort(end-1);
X_nextbad_1n=X(:,F_index(end-1));
% 计算形心
Xc_n1=1/Num_var_f*sum(X(:,F_index(1:end-1)),2);
f_Xc_n1=double(subs(f,symvar(f),Xc_n1’));
% 计算精度与迭代次数
m=abs(double(subs(f,symvar(f),X(:,F_index(end))‘))-f_Xc_n1);
n=n+1;
% 运算数据记录
end
%% 结果输出
minx=X_best_0;
ff=120*X_best_0(1,1)+X_bes
约束条件判断子函数
judge子函数代码:
judge子函数如下:
function [J]=judge(x1,x2)
g1=1-0.25*x2;%
g2=1-7/45*x1*x2;
g3=1-7/45*x1^3*x2;
g4=1-1/320*x1*x2^2;%
g5=-x1;%
g6=-x2;
% 可行域条件
if g1《=0&&g2《=0&&g3《=0&&g4《=0&&g5《=0&&g6《=0
J=1
else
J=0
end
运算结果与可行域
程序运行结果为:最优点(0.7217,21.0939),此时f= 107.6936。此时程序所取eps=5
可行域图与最优点于图上标记:



 举报
举报






 举报
举报

