

基于集成学习的决策介绍(下)
电子说
描述
4.2 细节
4.2.1 损失函数
Adaboost 模型是加法模型,学习算法为前向分步学习算法,损失函数为指数函数的分类问题。
加法模型:最终的强分类器是由若干个弱分类器加权平均得到的。
前向分布学习算法:算法是通过一轮轮的弱学习器学习,利用前一个弱学习器的结果来更新后一个弱学习器的训练集权重。第 k 轮的强学习器为:
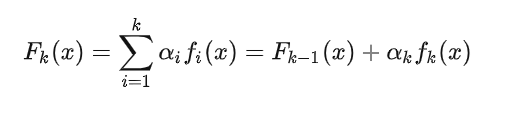
定义损失函数为 n 个样本的指数损失函数:

利用前向分布学习算法的关系可以得到:

因为  已知,所以令
已知,所以令  ,随着每一轮迭代而将这个式子带入损失函数,损失函数转化为:
,随着每一轮迭代而将这个式子带入损失函数,损失函数转化为:

我们求  ,可以得到:
,可以得到:

将  带入损失函数,并对
带入损失函数,并对 求导,使其等于 0,则就得到了:
求导,使其等于 0,则就得到了:

其中,  即为我们前面的分类误差率。
即为我们前面的分类误差率。

最后看样本权重的更新。利用  和
和  ,即可得:
,即可得:
这样就得到了样本权重更新公式。
4.2.2 正则化
为了防止 Adaboost 过拟合,我们通常也会加入正则化项,这个正则化项我们通常称为步长(learning rate)。对于前面的弱学习器的迭代
加上正则化项  我们有:
我们有:

 的取值范围为 0<
的取值范围为 0< ≤1 。对于同样的训练集学习效果,较小的
≤1 。对于同样的训练集学习效果,较小的  意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。
意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。
4.3 优缺点
4.3.1 优点
- 分类精度高;
- 可以用各种回归分类模型来构建弱学习器,非常灵活;
- 不容易发生过拟合。
4.3.2 缺点
- 对异常点敏感,异常点会获得较高权重。
5. GBDT
GBDT(Gradient Boosting Decision Tree)是一种迭代的决策树算法,该算法由多棵决策树组成,从名字中我们可以看出来它是属于 Boosting 策略。GBDT 是被公认的泛化能力较强的算法。
5.1 思想
GBDT 由三个概念组成:Regression Decision Tree(即 DT)、Gradient Boosting(即 GB),和 Shrinkage(一个重要演变)
5.1.1 回归树(Regression Decision Tree)
如果认为 GBDT 由很多分类树那就大错特错了(虽然调整后也可以分类)。对于分类树而言,其值加减无意义(如性别),而对于回归树而言,其值加减才是有意义的(如说年龄)。GBDT 的核心在于累加所有树的结果作为最终结果,所以 GBDT 中的树都是回归树,不是分类树,这一点相当重要。
回归树在分枝时会穷举每一个特征的每个阈值以找到最好的分割点,衡量标准是最小化均方误差。
5.1.2 梯度迭代(Gradient Boosting)
上面说到 GBDT 的核心在于累加所有树的结果作为最终结果,GBDT 的每一棵树都是以之前树得到的残差来更新目标值,这样每一棵树的值加起来即为 GBDT 的预测值。
模型的预测值可以表示为:

 为基模型与其权重的乘积,模型的训练目标是使预测值
为基模型与其权重的乘积,模型的训练目标是使预测值  逼近真实值 y,也就是说要让每个基模型的预测值逼近各自要预测的部分真实值。由于要同时考虑所有基模型,导致了整体模型的训练变成了一个非常复杂的问题。所以研究者们想到了一个贪心的解决手段:每次只训练一个基模型。那么,现在改写整体模型为迭代式:
逼近真实值 y,也就是说要让每个基模型的预测值逼近各自要预测的部分真实值。由于要同时考虑所有基模型,导致了整体模型的训练变成了一个非常复杂的问题。所以研究者们想到了一个贪心的解决手段:每次只训练一个基模型。那么,现在改写整体模型为迭代式:

这样一来,每一轮迭代中,只要集中解决一个基模型的训练问题:使  逼近真实值 y 。
逼近真实值 y 。
举个例子:比如说 A 用户年龄 20 岁,第一棵树预测 12 岁,那么残差就是 8,第二棵树用 8 来学习,假设其预测为 5,那么其残差即为 3,如此继续学习即可。
那么 Gradient 从何体现?其实很简单,其残差其实是最小均方损失函数关于预测值的反向梯度(划重点):

也就是说,预测值和实际值的残差与损失函数的负梯度相同。
但要注意,基于残差 GBDT 容易对异常值敏感,举例:

很明显后续的模型会对第 4 个值关注过多,这不是一种好的现象,所以一般回归类的损失函数会用绝对损失或者 Huber 损失函数来代替平方损失函数。

GBDT 的 Boosting 不同于 Adaboost 的 Boosting,GBDT 的每一步残差计算其实变相地增大了被分错样本的权重,而对与分对样本的权重趋于 0,这样后面的树就能专注于那些被分错的样本。
5.1.3 缩减(Shrinkage)
Shrinkage 的思想认为,每走一小步逐渐逼近结果的效果要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它并不是完全信任每一棵残差树。
Shrinkage 不直接用残差修复误差,而是只修复一点点,把大步切成小步。本质上 Shrinkage 为每棵树设置了一个 weight,累加时要乘以这个 weight,当 weight 降低时,基模型数会配合增大。
5.2 优缺点
5.2.1 优点
- 可以自动进行特征组合,拟合非线性数据;
- 可以灵活处理各种类型的数据。
5.2.2 缺点
- 对异常点敏感。
5.3 与 Adaboost 的对比
5.3.1 相同:
- 都是 Boosting 家族成员,使用弱分类器;
- 都使用前向分布算法;
5.3.2 不同:
- 迭代思路不同:Adaboost 是通过提升错分数据点的权重来弥补模型的不足(利用错分样本),而 GBDT 是通过算梯度来弥补模型的不足(利用残差);
- 损失函数不同:AdaBoost 采用的是指数损失,GBDT 使用的是绝对损失或者 Huber 损失函数;
6. 参考
-
机器学习算法中 GBDT 与 Adaboost 的区别与联系是什么? - Frankenstein 的回答 - 知乎
-
为什么说bagging是减少variance,而boosting是减少bias
-
Ensemble Learning - 周志华
- 相关推荐
-
机器学习中常用的决策树算法技术解析2020-10-12 1311
-
不可错过 | 集成学习入门精讲2018-06-06 0
-
决策树在机器学习的理论学习与实践2019-09-20 0
-
机器学习的决策树介绍2020-04-02 0
-
介绍支持向量机与决策树集成等模型的应用2021-09-01 0
-
决策树的生成资料2023-09-08 0
-
决策树的介绍2016-09-18 543
-
机器学习的决策渗透着偏见,能把决策权完全交给机器吗?2018-05-11 1479
-
决策树的原理和决策树构建的准备工作,机器学习决策树的原理2018-10-08 6004
-
决策树的基本概念/学习步骤/算法/优缺点2021-01-27 2636
-
为什么要使用集成学习 机器学习建模的偏差和方差2021-08-14 3000
-
强化学习与智能驾驶决策规划2023-02-08 1857
-
基于集成学习的决策介绍(上)2023-02-17 745
-
基于 Boosting 框架的主流集成算法介绍(下)2023-02-17 2811
-
什么是集成学习算法-12023-02-24 1216
全部0条评论

快来发表一下你的评论吧 !

