

SVPWM原理推导与Mathcad建模的基本概念
工业控制
描述
1.概述:
SVPWM由于直流电压利用率高,谐波含量少,易于数字化控制。随着近年来SVPWM的发展,已经脱离了交流电机磁链轨迹控制的原意,形成了电力电子技术中的一类PWM控制方式。用Mathcad搭建模型从三相逆变器拓扑结构与数学概念出发,来理解并阐述SVPWM。
2.基本概念:
学习SVPWM之前需要引入一些基本概念,即相量、矢量、空间、时间。
相量
表征稳态正弦量三要素,幅值、频率、初相位。即可以写出正弦量的瞬时值表达式,也称解析式,通过解析式可画出波形图。
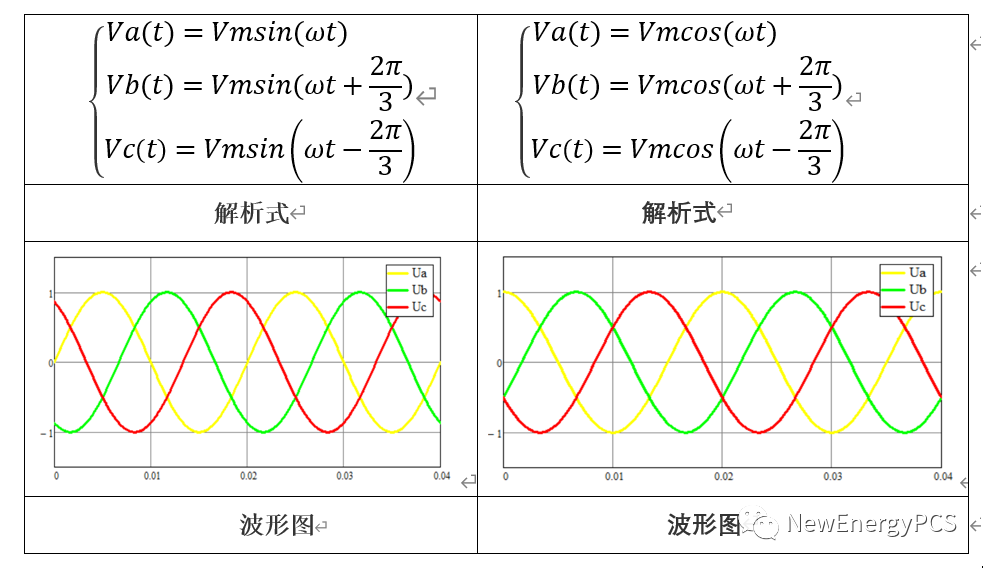
Va、Vb、Vc、幅值最大值都是Vm,角频率均为ω,初相φ0分别是0,2π/3,-2π/3, 可以发现要对正弦量进行运算,无论是用波形图还是瞬时值表达式,均是正弦函数之间运算很不方便,为此人为定义了相量,引入正弦量的相量表示。
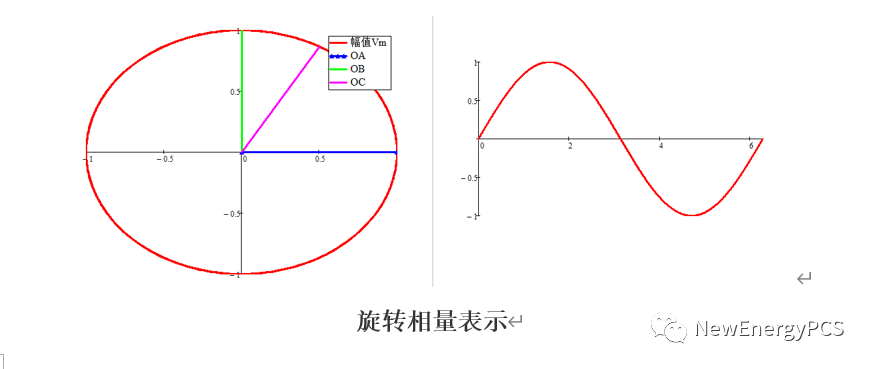
如上图所示,在直角坐标系内,作一条有向线段OA,其长度为正弦幅值最大值Vm,它的起始位置与x轴正方向的夹角等于初相,并以正弦交流电的角频率ω为角速度逆时针匀速旋转,则在任一瞬间旋转相量与x轴的夹角即为正弦交流电的相位,它在y轴的投影即为该正弦交流电的瞬时值。此时用旋转相量能完全反映正弦量的三要素及变化规律。
应用相量图时注意 :
- 同一相量图中,各正弦交流电的频率相同
- 同一相量图中,相同单位的相量应按相同比例画出
- 取直角坐标轴的水平正方向为参考方向即逆时针转动角度为正,反之为负。
- 相量表示正弦量后,它们的加、减运算可按平行四边形法则进行。
- 相量图、波形图、解析式是正弦量的不同表示方法,有对应关系,但在数学并上不相等。
可得结论1:
相量表示的正弦量,要区分Va、Vb、Vc,只需要将它们的初相位单独标识出来,即Va、Vb、Vc,可分别记为∠0,∠-120°,∠120°。在相同威廉希尔官方网站 系统中一般频率相同,幅度大小变化,故初相位的基础上加上幅值信息,就是这个系统的相量表达。即Va=Vm∠0,Vb= Vm∠-120,Vc= Vm∠120
可得结论2:
通过使用旋转相量表示正弦量,可以发现正弦量运算转换到非常简单的系统中了,可以看出相量的表示,实际是把正弦量转换到了极坐标表示。这样就可以用欧拉公式非常方便的运算。
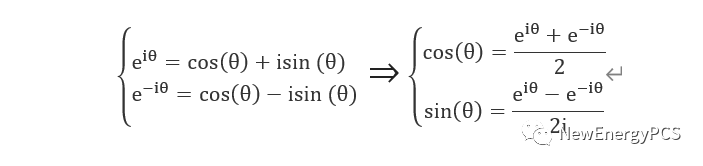

矢量
在物理学中,曾学习过速度矢量、力矢量等,它们都是即有大小、又有方向的向量,一般称它们为空间矢量,其加、减运算遵循平行四边形法则。用以表示稳态正弦量的旋转相量与力学中的矢量不同,它只是相位随时间变化的量,虽然加、减运算也遵循平行四边形法则,但与方向无关。可以看到相量代表矢量,有着明确的物理意义。不过矢量也是向量,其大小可以表示幅值,其方向可以表示相位。
空间
任何矢量都必须存在于某一个空间,相量这个定义的矢量也是,它的矢量空间就是复平面。例如在ABC空间,有ABC三个轴,这个三个轴上的基地长度都是1,方向依次增加120°。同时有幅值为1的三相对称正弦量ua、ub、uc,相位依次滞后120°,将其记为“adc系统”。
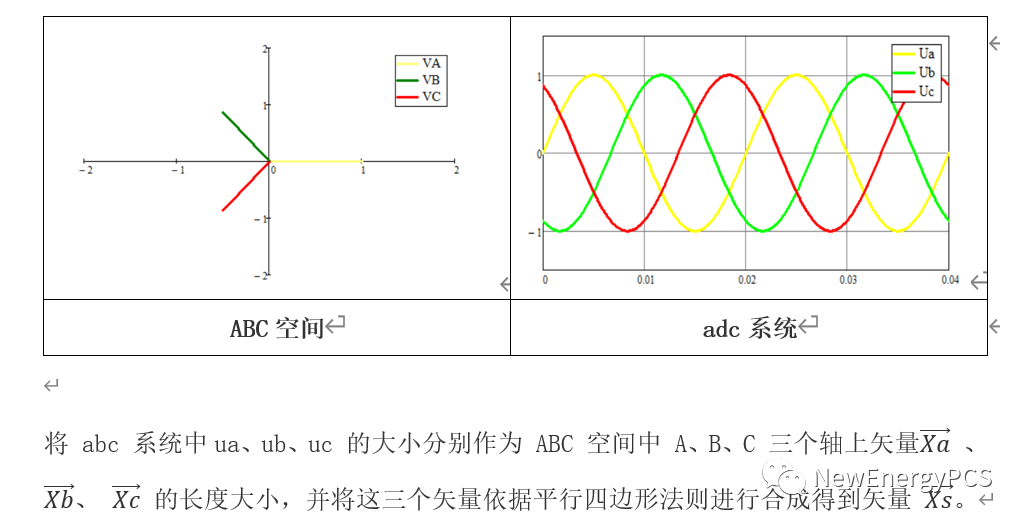
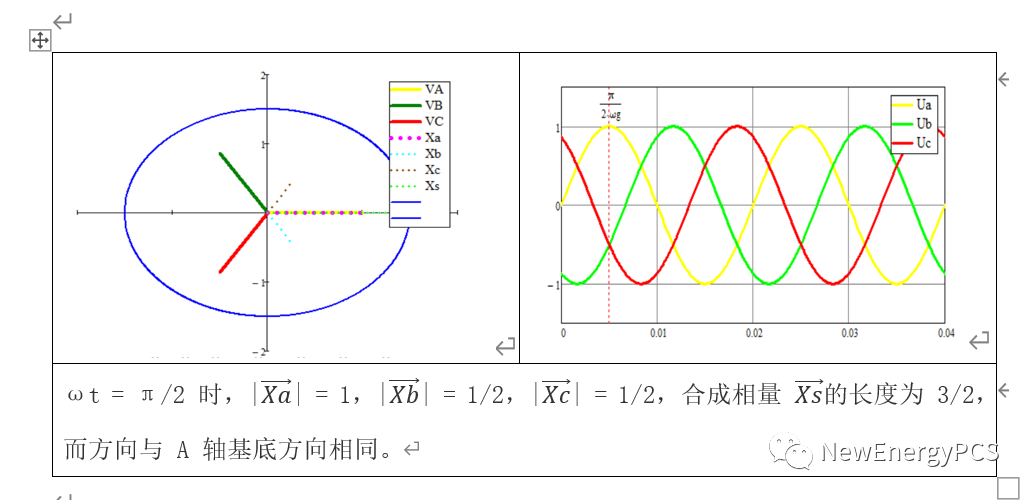
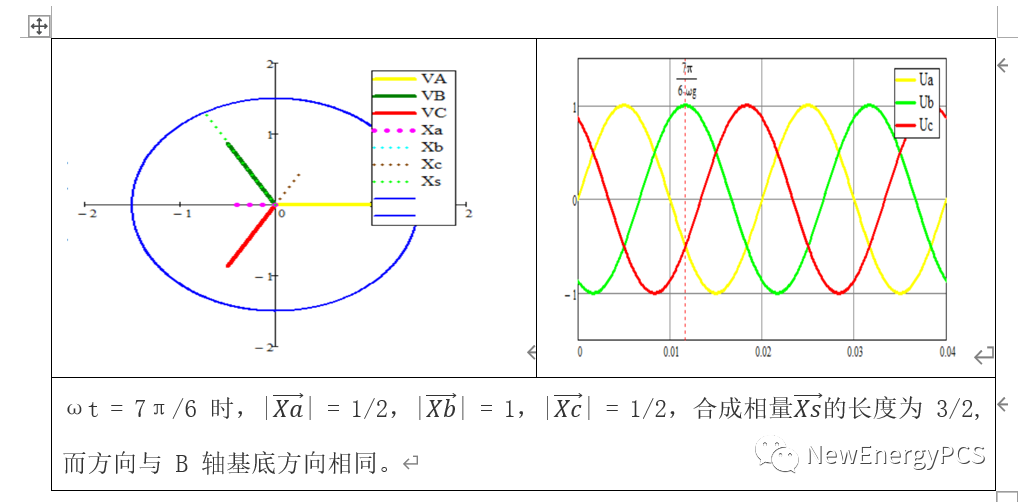
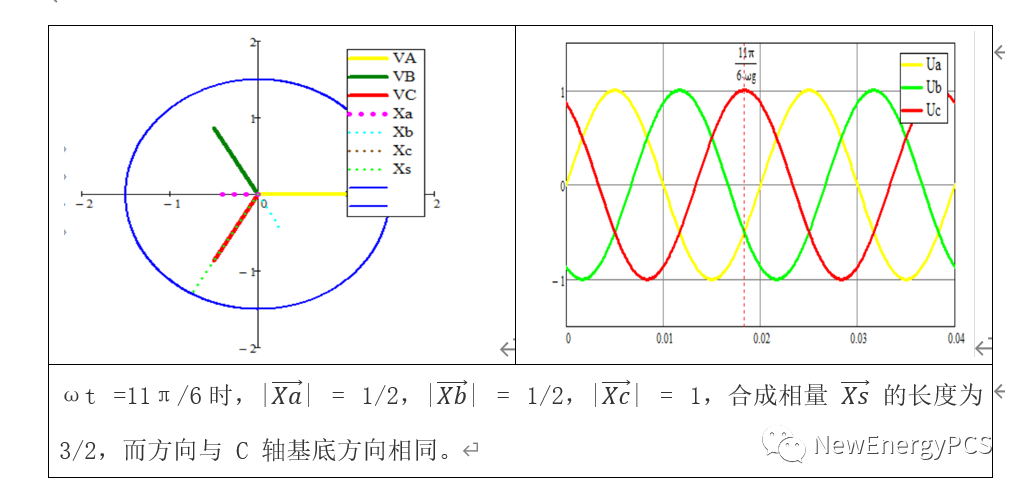
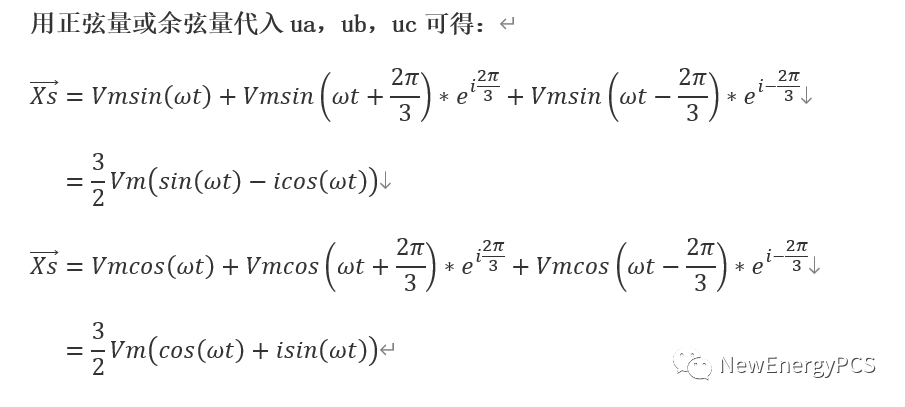
结论:
上式可以证明合成矢量是一个长度保持 3/2 不变 且在空间中匀速旋转的矢量,旋转方向为逆时针方向,旋转速度等于 abc 系统中角频率 ω。这里分别用sin与cos求证,是因为sin与cos存在π/2相位差,clark变换会导致α轴与β轴不一样。
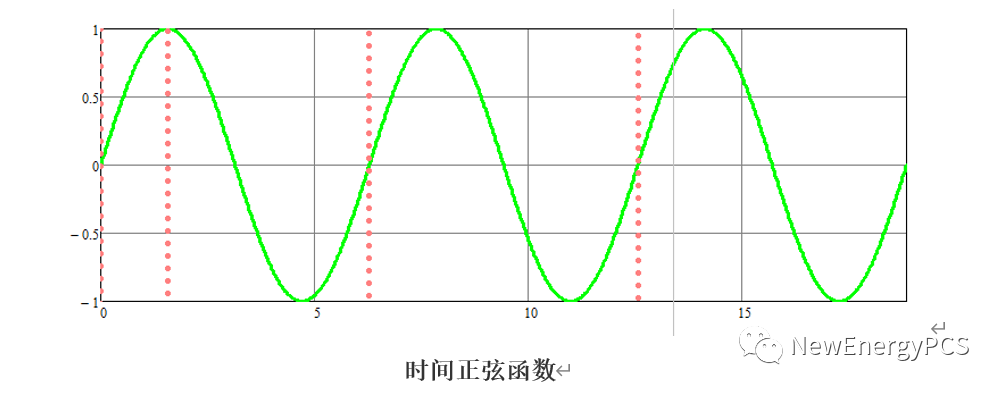
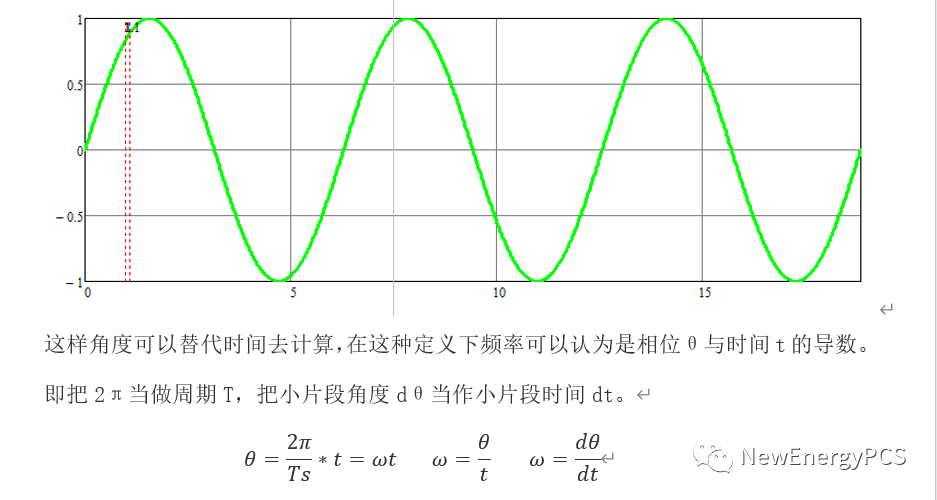
时间
在对正弦稳态信号的分析中,时间信息其实是和频率信息高度捆绑在一起的,在相量表达中,时间信号伴随着频率系统一起被省略。而在空间矢量系统中(旋转相量),频率和时间则可以被拿出来讨论,但是这里的频率并不是正弦稳态信号中的频率,而是空间矢量旋转的角速度。

-
Fpga Cpld的基本概念2012-08-20 0
-
C语言基本概念2015-08-01 0
-
SVPWM的原理推导和控制算法详解2016-01-28 0
-
人工智能基本概念机器学习算法2021-09-06 0
-
DCDC变换器建模2021-10-29 0
-
SVPWM的原理及法则推导和控制算法介绍2023-10-07 0
-
SVPWM的原理及法则推导和控制算法详解2016-04-13 793
-
基于Mathcad的LLC公式推导与化简(1)2023-06-23 6354
-
基于Mathcad的LLC公式推导与化简(2)2023-06-23 3979
-
SVPWM原理推导与Mathcad建模的坐标变换2023-07-10 2072
-
基于载波的SVPWM发波计算Mathcad实例2023-07-10 2272
-
基于载波SVPWM与空间矢量SVPWM实现策略的等效推导2023-07-10 1841
-
SVPWM原理推导与Mathcad建模控制实现2023-07-10 2312
-
SVPWM原理推导与Mathcad建模-基本概念2023-10-20 1803
全部0条评论

快来发表一下你的评论吧 !

