
资料下载

关于马尔科夫随机场的文献
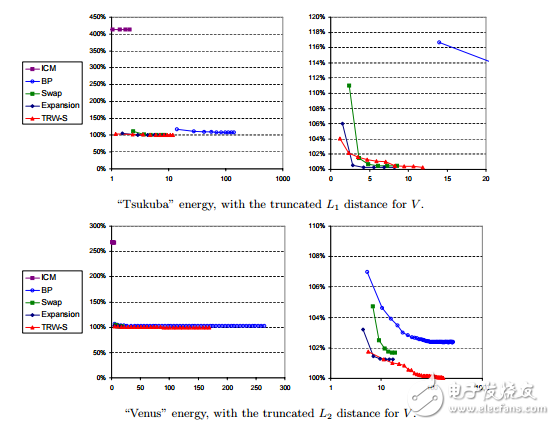
1 Introduction Many problems in early vision involve assigning each pixel a label, where the labels represent some local quantity such as disparity. Such pixel labeling problems are naturally represented in terms of energy minimization, where the energy function has two terms: one term penalizes solutions that are inconsistent with the observed data, while the other term enforces some kind of spatial coherence. One of the reasons this framework is so popular is that it can be justified in terms of maximum a posteriori estimation of a Markov Random Field, as described in [1, 2]。 Despite the elegance and power of the energy minimization approach, its early adoption was slowed by computational considerations. The algorithms that were originally used, such as ICM [1] or simulated annealing [3, 4], proved to be extremely inefficient. In the last few years, energy minimization approaches have had a renaissance, primarily due to powerful new optimization algorithms such as graph cuts [5, 6] and Loopy Belief Propagation (LBP) [7, 8]。 The results, especially in stereo, have been dramatic; according to the widely-used Middlebury stereo benchmarks [9], almost all the top-performing stereo methods rely on graph cuts or LBP. Moreover, these methods give substantially more accurate results than were previously possible. Simultaneously, the range of applications of pixel labeling problems has also expanded dramatically, moving from early applications such as image restoration [1], texture modeling [10], image labeling [11], and stereo matching [4, 5], to applications such as interactive photo segmentation [12–14] and the automatic placement of seams in digital photomontages [15]。 Relatively little attention has been paid, however, to the relative performance of various optimization algorithms. Among the few exceptions is [16], which compared graph cuts and LBP, and [17], which compared several different max flow algorithms for graph cuts. While it is generally accepted that algorithms such as graph cuts are a huge improvement over older techniques such as simulated annealing, less is known about the efficiency vs. accuracy tradeoff amongst more recently developed algorithms. In this paper, we evaluate a number of different energy minimization algorithms for pixel labeling problems. We propose a number of benchmark problems for energy minimization and use these benchmarks to compare several different energy minimization methods. Since much of the work in energy minimization has been motivated by pixel labeling problems over 2D grids, we have restricted our attention to problems with this simple topology. (The extension of our work to more general topologies, such as 3D, is straightforward.) This paper is organized as follows. In section 2 we give a precise description of the energy functions that we consider, and present a simple but general software interface to describe such energy functions and to call an arbitrary energy minimization algorithm. In section 3 we describe the different energy minimization algorithms that we have implemented, and in section 4 we present our set of benchmarks. In section 5 we provide our experimental comparison of the different energy minimization methods. Finally, in section 6 we discuss the conclusions that can be drawn from our study.
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章




